До сих пор мы рассматривали равновесие жидкостей и газов при наличии лишь гравитационных массовых сил — сил тяжести.
В практике имеет место равновесие жидкостей и газов при наличии негравитационных массовых сил — сил инерции и электромагнитных сил, действующих на проводящие среды. Общеё условие возможности существования равновесия, заключается в том, что массовые силы должны иметь потенциал, относится и ко всем негравитационным массовым силам.
Остановимся на двух случаях равновесия при наличии сил инерции.
Пример. Пусть сосуд, наполненный жидкостью, движется равноускоренно (или равнозамедленно) в горизонтальном направлении (рис. 2.5).
Из теоретической механики известно, что задачу динамики можно рассматривать как задачу статики, если к внешним силам прибавить силы инерции.

Если сосуд движется равноускоренно с ускорением а, то при выбранной системе координат проекции напряжений массовых сил будут
X = a; Y = 0; Z = g.
Уравнение (2.5) после интегрирования примет вид

Произвольная постоянная С определится из условия, что при х=x 0 и z = z0 давление будет р= ро, т. е.
 ,
,
следовательно, давление в любой точке жидкости определится по формуле

а уравнение поверхностей уровня (р =const) будет иметь вид  .
.
Если равноускоренное движение с ускорением а направлено вертикально вниз, то массовые силы, отнесенные к единице массы, будут
 и
и 
интеграл уравнения (2.5) будет равен
 .
.
Постоянная определится из условия, что при z = z0 р = ро
т.е.
 ,
,
тогда давление в любой точке жидкости равно
 . (2.15)
. (2.15)
Уравнение поверхностей уровня будет z = const.
Из сравнения соотношения (2.15) с формулой (2.9) видим, что при таком движении уменьшается суммарное ускорение, а при а = g жидкость будет невесомой.
Очевидно, что, изменив направление движения на обратное, при том же ускорении получим эффект обратный, как бы утяжеление жидкости. Это явление наблюдается при взлете ракеты.
Задание 1. У тягача - автомобиля в течение времени t равномерно изменяется скорость от V 1 до V 2 , в результате чего изменяется форма свободной поверхности жидкости, которой наполнена прицепленная к нему цистерна (рис. 2.6). Диаметр цистерны D , длина L . Плотность жидкости r .
Задание:
1. Вывести уравнение свободной поверхности жидкости.
2. Определить, на какую высоту повысится или понизится уровень жидкости у передней стенки цистерны (по ходу автомобиля – тягача).
3. Построить линию свободной поверхности жидкости.
4. Определить величину избыточного гидростатического давления в точке, обозначение которой указано в исходных данных.
| Исходные данные | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V 1 ,км/ч | 5 | 20 | 40 | 45 | 50 | 70 | 20 | 10 | 5 |
| V 2 , км/ч | 20 | 5 | 30 | 25 | 35 | 39 | 10 | 30 | 25 |
| t , с | 7 | 6 | 4 | 5 | 6 | 4 | 5.5 | 6 | 5 |
| L , м | 8.7 | 14.7 | 9.4 | 10 | 9,6 | 6,7 | 12 | 14 | 12 |
| D , м | 2,2 | 3 | 2 | 2,8 | 3 | 2,6 | 2,2 | 3 | 2 |
| r , кг/м3 | 890 | 900 | 950 | 830 | 800 | 9 00 | 830 | 790 | 850 |
| Точка | A | B | C | A | B | C | B | A | C |
Примечание:
1. Для вывода уравнения свободной поверхности жидкости необходимо воспользоваться уравнением равновесия жидкости в дифференциальной форме.
2.
 |
Горизонтальное ускорение а, м/с2, определяется по формуле
 .
.
Пример 2.
Рассмотрим равновесие жидкости, покоящейся относительно сосуда, равномерно вращающегося вокруг вертикальной оси с угловой скоростью w (рис. 2.7).
 Проекции сил на оси координат будут
Проекции сил на оси координат будут

а уравнение (2.5) после интегрирования примет вид
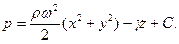
Произвольная постоянная определится из условия, что при

 .
.
Следовательно, гидростатическое давление равно

уравнение поверхностей будет

 Это уравнение есть уравнение параболоида вращения.
Это уравнение есть уравнение параболоида вращения.
Задание 2.
При отливке чугунного бандажа (рис. 2.8) для колеса форму, залитую расплавленным чугуном, вращают вокруг вертикальной оси для того, чтобы придать чугуну большую плотность. Диаметр бандажа D , превышение уровня жидкого чугуна в литнике над нижней точкой А бандажа при неподвижной форме равно Н, плотность расплавленного чугуна r =7000 кг/м3.
Требуется определить:
1. Избыточное гидростатическое давление в точке А при неподвижной форме.
2. Число оборотов n , с которой нужно вращать форму, чтобы давление в точке А возросло в k раз по сравнению с давлением в этой точке при неподвижной форме.
| Исходные данные | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D , м | 1 | 1,1 | 2,0 | 1,25 | 1,3 | 1,4 | 1,5 | 1,45 | 1,6 |
| Н, м | 0,15 | 0,2 | 0,25 | 0,3 | 0,45 | 0,35 | 0,4 | 0,2 | 0,25 |
| k | 10 | 20 | 30 | 15 | 25 | 12 | 24 | 30 | 35 |
Дата: 2018-11-18, просмотров: 775.