ОСНОВНЫЕ ПОЛОЖЕНИЯ ГИДРОМЕХАНИКИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

История развития науки

Происхождение науки гидравлики очень древнее. Явления, относящиеся к области гидравлики, интересовали человека еще в самые отдаленные времена. Многие вопросы, связанные с орошением, водоснабжением и использованием водной энергии для примитивных двигателей, решали в глубокой древности.

Основоположником гидравлики считают древнегреческого ученого Архимеда (384-322 до н.э.), который написал трактат “О плавающих телах”. Большой вклад в развитие гидравлики внесли Леонардо да Винчи (1452-1519), Галилей (1564-1642), Паскаль (1623-1662). Итальянский ученый Торричелли - ученик Галилея открыл закон истечения жидкости из сосуда и дал формулу, определяющую скорость истечения жидкости. Французский ученый Паскаль опубликовал в 1650 г. закон о передаче внешнего давления в жидкости, а в 1687 г. английский ученый Ньютон (1642-1727) сформулировал закон внутреннего трения в движущейся жидкости.

Гидравлика как самостоятельная наука начала формироваться в XVIII в. после работ, выполненных в Петербургской академии наук М. В. Ломоносовым (1711-1765), Д. Бернулли(1700-1782) и Л. Эйлером (1707-1783), которые разработали основные законы движения жидкости. В 1738 г. Д. Бернулли опубликовал книгу “Гидродинамика”. Даниил Бернулли впервые ввел термин «гидромеханика». Он установил зависимость между удельными энергими при движении жидкости, которая в настоящее время называется уравнением Бернулли. Кроме того, он исследовал задачу о давлении струи жидкости на пластину.

В 1748 г. М. В. Ломоносов впервые изложил открытый им закон сохранения энергии. В 1755 г. Л. Эйлер вывел дифференциальные уравнения равновесия и движения жидкостей.

Дальнейший этап в истории развития гидромеханики, объединяющий конец XVIII и начало XIX веков, характерен математической разработкой гидродинамики идеальной жидкости. В этот период вышли труды французских математиков Лагранжа (1736 - 1813) и Коши (1789 - 1857), посвященные потенциальным плоским потокам, теории волн малой амплитуды и др.

Основы теории движения вязкой жидкости были заложены французским ученым Навье (1785—1836) и английским физиком и математиком Стоксом (1819—1903). Поэтому уравнения движения вязкой жидкости называются уравнениями Навье— Стокса.

В 1881 г. профессор Казанского университета И. С. Громеко (1851—1889) опубликовал работу «Некоторые случаи движения несжимаемой жидкости», в которой дал новую форму уравнений движения жидкости, удобную для получения энергетических зависимостей. Им же впервые было проведено теоретическое исследование нестационарного движения жидкости в капиллярах.

Большую роль в развитии гидравлики сыграли русские ученые: Н. П. Петров, Н. Е. Жуковский (1847-1921), В. Г. Шухов исследования которых в области механики жидкости стали классическими. В 1883 г. Н. П. Петров разработал гидродинамическую теорию смазки. Опубликованная в 1889 г. работа русского ученого Н. Е. Жуковского “О гидравлическом ударе в водопроводных трубах” получила мировую известность.

Из многочисленных экспериментальных исследований движения жидкости в трубах укажем на опыты с трубками малого диаметра французского врача и испытателя Пуазёйля (1799—1869), изучавшего движение крови в сосудах, и опыты английского физика Рейнольдса (1842—1912), установившего в 1883 г. закон подобия течений в трубах.

Целую эпоху в истории развития гидромеханики составляют исследования по воздухоплаванию, включающие разработку теории полета самолетов и ракет. Результаты этих исследований были изложены в трудах выдающихся русских ученых Д. И.Менделеева (1834—1907),Н. Е. Жуковского и С. Д. Чаплыгина (1869—1942). В 1880 г, Д. И. Менделеев опубликовал работу «О сопротивлении жидкостей и воздухоплавании», в которой были высказаны важные положения о механизме сопротивления движению тел в жидкости и даны основные представления о пограничном слое. Созданию теории крыла и воздушного винта были посвящены исследования Н. Е. Жуковского. В 1906 г. он разработал теорию подъемной силы крыла, имеющую большое значение.

Дальнейшее развитие гидромеханики широко используется при создании современных машин различного назначения с гидроприводом, в том числе технологических

Повышение технического уровня гидрофицированных технологических: кузнечно-прессовых, металлургических и подъёмно-транспортных машин основано прежде всего на применении современного гидрооборудования и средств гидроавтоматики, обладающих высокими основными параметрами и показателями надежности. К важнейшим показателям, характеризующим эксплуатационные свойства гидрооборудования данных машин, относятся диапазон регулирования и работоспособность в широком интервале изменения температур воздуха и рабочей жидкости, а также возможность дистанционного и автоматического управления исполнительными механизмами машин. При разработке данного пособия были приняты во внимание работы по разработке, созданию и применению гидроприводов на промышленных предприятиях города Магнитогорска. В частности, учтен опыт использования элементов и систем гидроприводов технологических машин таких широко известных фирм, как “MANNESMAN REXROTH”, “BOSH”, “HITACHI”, “MOOG” на Магнитогорском металлургическом комбинате, а также в подъемно-транспортных, строительных, дорожных машинах различных фирм, используемых в тресте “Магнитострой“.

МГ-46-Б

Классификация гидравлических масел по DIN 51524

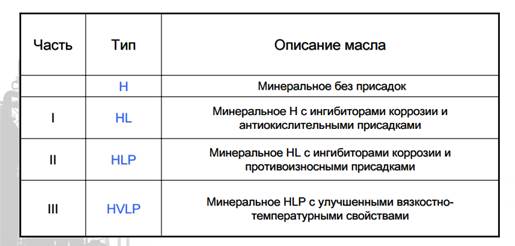
Классификация гидравлических жидкостей по DIN 51502

Классификация гидравлических жидкостей по ISO 11158

Классификация вязкости индустриальных масел по ISO

. В таблице приведены характеристики некоторых типов жидкостей, применяемых в промышленных гидроприводах.

Рабочая жидкость	Плотность, кг/м³ (при 20°С)	Кинематическая вязкость мм²/с (при 50 °С)	Температура, °С
Рабочая жидкость	Плотность, кг/м³ (при 20°С)	Кинематическая вязкость мм²/с (при 50 °С)	вспышки	застывания
Минеральные масла
АМГ-10 (ГОСТ 6794-75*)	850	10	93	-70
МГЕ-10А	855	10	96	-70
Индустриальные масла (ТУ 38 101413-78)
ИГП-18	880	18	170	-15
ИГП-38	900	35	210	-15
Турбинные масла
T22 (ГОСТ .32- 74)	900	22	1180	-15
Силиконовая жидкость
7-50C-3 (ГОСТ 20734-75)	935	10	180	-70
Водно-гликолевая жидкость
ПГВ (ГОСТ25821-83)	1151	13	-	-50
Водно-глицериновые жидкости
Промгидрол П-20 М-1 (ТУ 6-02-1140-78)	1125	20	-	-30

Окисление масла приводит к изменению его вязкости (как правило, к повышению) и к накоплению в нем продуктов окисления, образующих осадки и лаковые отложения на поверхностях деталей гидросистемы, что затрудняет ее работу.

Повышение антиокислительных свойств гидравлических масел достигают путем введения антиокислительных присадок обычно фенольного и аминного типов.

· Кислотное число - TAN (total acid number). В процессе эксплуатации накапливаются продукты окисления масла. Данное число определяется количеством (мг) едкого калия, необходимого для нейтрализации кислот в 1 г масла. Максимально кислотное число в процессе эксплуатации не должно превышать 30% (в состоянии поставки).

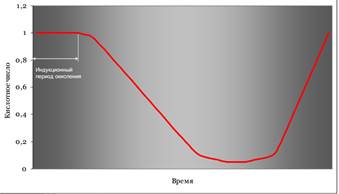
· Большое значение для гидроприводов технологических машин, работающих на открытом воздухе, имеет величина температуры замерзания жидкости и ее стабильность.

В гидроприводах промышленных роботов, работающих в закрытых отапливаемых помещениях, в качестве рабочих жидкостей обычно применяют минеральные масла вязкостью до 40 мм²/с и со степенью очистки не менее 25 мкм, а для следящих систем - не менее 10 мкм.

Для промышленных роботов, работающих в условиях повышенных или пониженных температур, необходим подбор соответствующих жидкостей.

ОСНОВЫ ГИДРОСТАТИКИ

Пример 2.

Рассмотрим равновесие жидкости, покоящейся относительно сосуда, равномерно вращающегося вокруг вертикальной оси с угловой скоростью w (рис. 2.7).

Проекции сил на оси координат будут

а уравнение (2.5) после интегрирования примет вид

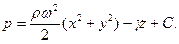
Произвольная постоянная определится из условия, что при

Следовательно, гидростатическое давление равно

уравнение поверхностей будет

Это уравнение есть уравнение параболоида вращения.

Задание 2.

При отливке чугунного бандажа (рис. 2.8) для колеса форму, залитую расплавленным чугуном, вращают вокруг вертикальной оси для того, чтобы придать чугуну большую плотность. Диаметр бандажа D , превышение уровня жидкого чугуна в литнике над нижней точкой А бандажа при неподвижной форме равно Н, плотность расплавленного чугуна r =7000 кг/м³.

Требуется определить:

1. Избыточное гидростатическое давление в точке А при неподвижной форме.

2. Число оборотов n , с которой нужно вращать форму, чтобы давление в точке А возросло в k раз по сравнению с давлением в этой точке при неподвижной форме.

Исходные данные	0	1	2	3	4	5	6	7	8
D , м	1	1,1	2,0	1,25	1,3	1,4	1,5	1,45	1,6
Н, м	0,15	0,2	0,25	0,3	0,45	0,35	0,4	0,2	0,25
k	10	20	30	15	25	12	24	30	35

Задача.

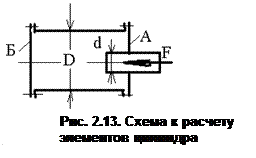Определить (рис. 2.13) нагрузку на болты крышек А и Б гидравлического цилиндра диаметром D =160 мм, если к плунжеру диаметром d =120 мм приложена сила F =20 кН.

Решение.

Давление в цилиндре р=F/(pd²/4)=4*20000/(p*0.12²)=1.77МПа.

Сила на крышку Б: F_Б= (pD²/4)*p =(p*0.16²/4)*1770000=36кН.

Сила на крышку А: F_А=(pD²/4 -pd²/4)*р =36000-20000=16кН.

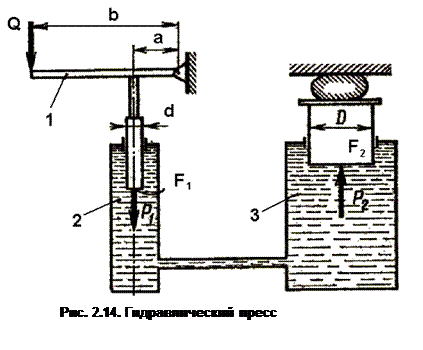
Гидравлический пресс

В практике существуют гидравлические машины, действие которых основано на применении законов гидромеханики, в частности на законе Паскаля. На рис. 2.14 представлена схема простейшего гидравлического пресса. С помощью такого устройства можно получить значительный выигрыш в силе. Гидравлический пресс состоит из следующих основных частей: рычага 1, малого цилиндра 2 с поршнем диаметром d, большого цилиндра 3 с поршнем диаметром D. Прикладывая к рычагу силу Q, действуем на малый поршень силой Р₁. В результате этого жидкость сжимается и давление передается на поршень большего цилиндра. Сила давления на поршень диаметром D равна Р₂. Зная: соотношения длин рычагов а, в; диаметры цилиндров; коэффициент полезного действия пресса, учитывающий потери на трение (h=0,8 – 0,85) можно получить расчетную формулу гидравлического пресса в виде:

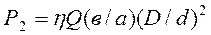Задача: Определить усилие Q , которое следует приложить к рычагу гидравлического пресса для получения усилия Р₂=200кН, если известно: в=1м, а=0,1 м, D =300 мм, d =30 мм, h =0,8.

Решение.

Используя предыдущую зависимость, можно относительно силы приложенной к рычагу записать: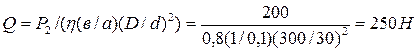

Закон Архимеда

Рассмотрим силы давления жидкости на тело, погруженное в эту жидкость (рис. 2.15, а).

Тело призматической формы имеет высоту h и площадь верхнего и нижнего оснований w. Верхнее основание погружено в жидкость на глубину h ₁ , нижнее — на глубину h ₂. При этом на тело действуют:

сила гидростатического давления жидкости на верхнее основание

сила гидростатического давления жидкости на нижнее основание

силы давления жидкости на боковые поверхности (грани призмы) не учитываются, так как они взаимно уравновешены.

Равнодействующая сил гидростатического давления равна разности сил P ₁ и P₂ и направлена вверх (в сторону большей) силы):

или

Таким образом, на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом. Это и есть закон Архимеда, открытый им в 250 г. до н. э.

Закон Архимеда справедлив для тел любой фирмы, так как тело другой, отличающейся от призматической и более сложной формы можно представить состоящим из бесконечного множества элементарных вертикальных призм.

МЕХАНИКА ТЕЧЕНИЯ ЖИДКОСТИ

Раздел технической гидромеханики, изучающий законы движения жидкости, называется гидродинамикой.

Расход жидкости

Потоки жидкости в общем случае являются трехмерными или объемными. Более простыми являются двухмерные и одномерные осевые. В технической гидромеханике рассматриваются одномерные потоки.

Объем жидкости V, проходящей через живое сечение трубопровода в единицу времени t, называют расходом

Q= V/t.

Расход – один из основных параметров технической гидромеханики и гидропривода. Единицей измерения его - м³/с. Часто в гидроприводе применяют – л/мин.

Средняя скорость движения потока через сечение S

v=Q/S.

Основные понятия струйчатого движения

Траекторией жидкой частицы называют кривую линию, которую описывает жидкая частица при движении. При этом жидкой частицей называют такой малый объем жидкости, для которого можно пренебречь изменением его формы.

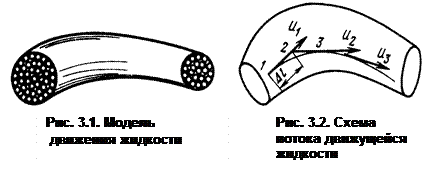
При решении практических задач предполагают, что поток движущейся жидкости состоит из элементарных струек, не меняющих своей формы, т. е. поток мысленно разбивают на ряд элементарных струек (трубок), как это показано на рис. 3.1. Модель, согласно такому предположению, называют струйчатой моделью движения жидкости.

Рассмотрим поток жидкости, находящейся в установившемся Движении (рис. 3.2). В точках 1, 2, 3, ... этого потока, взятых на расстоянии Dl друг от друга, проведем векторы U₁, U₂, U₃..., показывающие величину и направление скоростей движения частиц жидкости в данный момент времени. Касательная кривая, проведенная к векторам движения частиц жидкости и характеризующая направление движения ряда последовательно расположенных частиц в жидкости в данный момент времени, называется линией тока. В отличие от траектории, которая показывает путь движения одной частицы жидкости за определенный промежуток времени D t , линия тока соединяет разные частицы и дает некоторую мгновенную характеристику движущейся жидкости за время t.

Если в движущейся жидкости выделить бесконечно малый замкнутый контур и через все его точки провести линии тока, соответствующие данному моменту времени, то получится как бы трубчатая непроницаемая поверхность, называемая трубкой тока. Масса жидкости, движущейся внутри трубки тока, образует элементарную струйку.

Элементарная струйка обладает двумя свойствами:

1 ) скорости и площади поперечных сечений струек в одном живом сечении не меняются вследствие их малости;

2) скорости и площади поперечных сечений струек в различных живых сечениях могут меняться, однако произведение скорости v отдельных частиц струйки на площади их поперечного сечения S остаются постоянными (уравнение неразрывности элементарной струйки).

Таким образом, поток жидкости есть совокупность элементарных струек, представляющая собой непрерывную массу частиц, движущихся в каком-либо направлении.

Закон неразрывности потока

Основное уравнение кинематики жидкости – уравнение неразрывности, которое вытекает из условия несжимаемости жидкости и сплошности движения.

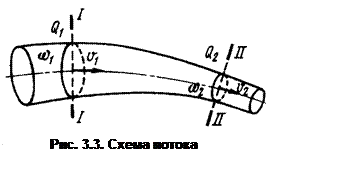
Рассмотрим установившееся движение в русле переменного сечения (рис. 3.3). Выберем два произвольных сечения /—/ и //—//, нормальных к оси потока, и рассмотрим участок потока, заключенный между сечениями.

При течении жидкости по трубопроводу переменного сечения без разрывов сплошности масса жидкости, проходящей через любое поперечное сечение канала, должна быть постоянной, т.е.

r₁w₁v₁= r₂S₂v₂=r_iw_iv_i=const

где v₁, v₂ — скорости жидкости в сечениях 1 и 2; w₁, w₂- площади двух поперечных сечений трубопровода; r₁, r₂ - плотности жидкости.

Если пренебречь сжимаемостью жидкости, то ее плотность в любом сечении будет одинакова и

v₁w₁= w₂v₂= w_iv_i=const,

что выражает закон неразрывности потока.

Энергия потока жидкости

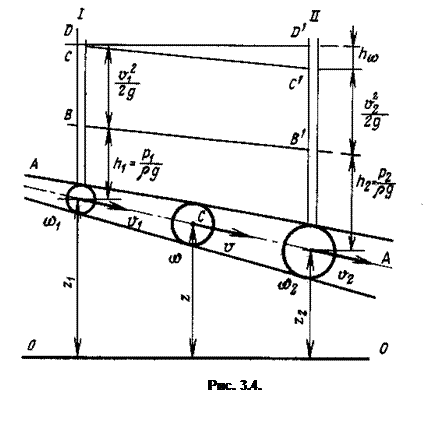
Учитывая, что поток жидкости представляет собой совокупность множества элементарных струек, и принимая движение потока установившимся или плавно изменяющимся, можно определить удельную энергию потока жидкости конечных размеров. Рассмотрим поток жидкости в виде наклонной трубы с плавно изменяющимся сечением (рис. 3.4). Внутри потока выделим некоторую точку с. Обозначим расстояние от этой точки до произвольно выбранной плоскости О - О (плоскость сравнения) -Z₁ , давление жидкости в центре тяжести сечения — р, среднюю скорость движения жидкости в выбранном сечении — v.

Полная удельная энергия потока равна сумме удельной кинетической энергии потока Э_к и удельной потенциальной энергии Э_п,

Э_у= Э_к + Э_п,

Определим слагаемые правой части:

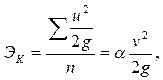
где п — число элементарных струек; и — скорости элементарных струек; v — средняя скорость потока; a — коэффициент, учитывающий неравномерность распределения скорости по сечению. 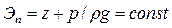, что, согласно гидростатическому закону,формулируется так:

для всех точек, данного объема покоящейся жидкости удельная потенциальная энергия относительно выбранной плоскости сравнения постоянна.

Тогда выражение для полной удельной энергии потока в выбранном сечении примет вид

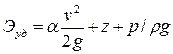Если использовать зависимость 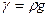,то

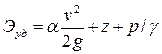Поскольку распределение скоростей в потоке неизвестно, то в гидравлике эти скорости принимаются одинаковыми, а при определении кинетической энергии потока вводится поправочный коэффициент a, учитывающий изменение кинетической энергии вследствие неравномерности распределения скоростей в живом селении потока. Коэффициент a называют коэффициентом кинетической энергии по имени ученого, открывшего его,— коэффициентом Кориолиса. Он может быть определен опытным путем, а при расчетах с достаточной точностью может приниматься: a=1,0—1,13 - для равномерных турбулентных потоков и a=2,0 - для равномерных ламинарных потоков.

Уравнение Бернулли

В потоке жидкости, движущейся в трубке с плавно изменяющимся сечением (см. рис. 3.4), выберем два произвольных сечения / и //. Обозначим р₁ и p ₂ давления в центрах тяжести сечений w₁ и w₂, v ₁ и v ₂ - средние скорости, а z ₁ и z₂—вертикальные координаты оси потока в выбранных сечениях.

Тогда величины полной удельной энергии потока в сечениях / и // соответственно могут быть записаны:

;

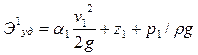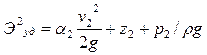При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается. Величину указанных потерь энергии обозначим h_w. Тогда баланс энергии в сечениях / и // можно записать так:

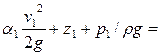
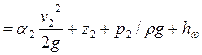Это уравнение называется уравнением Бернулли для реального потока жидкости. Оно устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением. Оно показывает, что за счет преобразования одного вида энергии в другой наблюдается при возрастании скорости уменьшение давления и, наоборот, при уменьшении скорости — возрастание давления.

Физический (энергетический) смысл уравнения Бернулли состоит в том, что при установившемся движении жидкости сумма трех удельных энергий (положения, давления и кинетической) остается неизменной.

Легко убедиться, что каждый член уравнения Бернулли имеет размерность длины и показывает:

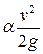- высоту скоростного напора; 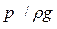пьезометрическую высоту, отсчитываемую в каждом сечении по пьезометру (см. рис. 3.4); z — геометрическую высоту; h_w — потерянный напор, равный части энергии, превращенной в тепло.

Сумма трех высот — скоростного напора, пьезометрической и геометрической — называется гидродинамическим напором:

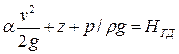Потери давления

При протекании по трубопроводу жидкость испытывает сопротивление, зависящее от длины трубы, шероховатости ее внутренних поверхностей, площади и формы поперечного сечения, что вызывает потери давления.

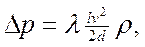В общем случае потери давления в трубах круглого сечения определяют по формуле Дарси-Вейсбаха:

где λ - коэффициент гидравлического трения; l - длина трубы; d - внутренний диаметр трубы.

Для ламинарного течения жидкости коэффициент гидравлического трения

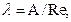
где А может иметь значения от 64 до 150 (например, в идеальном случае при изотермическом потоке А=64; при течение потока в реальных металлических трубах и гибких рукавах А=75…85; при небольшом изгибе рукавов А=108; при изгибе труб более 90° - А = 80; если поток движется по смятой на 40…50 % трубе, то А=150).

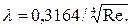Для турбулентного течения коэффициент гидравлического трения

Для определения коэффициентов гидравлического трения разработаны номограммы и таблицы.

Потери давления при ламинарном течении являются линейной функцией скорости (так как в выражении Re содержится скорость), а при турбулентном течении зависят от скорости в степени 1…2.

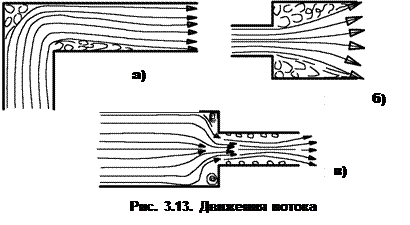
Кроме потерь давления по длине прямого трубопровода, в гидросистемах имеются потери на местных сопротивлениях: при повороте трубы (рис.3.13, а); при расширении (рис.3.13, б); сужении потока (рис.3.13, в); перекрытии труб аппаратурой управления и регулирования.

Потери давления (Па) на местном сопротивлении

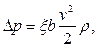
где x - коэффициент местного сопротивления; b - поправочный коэффициент.

Как правило, коэффициенты местных сопротивлений определяются экспериментальным путем и приводятся в справочниках. Например, для штуцеров x = 0,1; при повороте потока на 90° x =2; для гидроаппаратуры x = 1,0. ..4,0.

Поправочный коэффициент b учитывает зависимость потерь от числа Re при ламинарном течении. При Re >2300 b = 1, при Re = 400 b=2, при Re=100 b = 8, при Rе = 10 b = 80. Для нахождения суммарных потерь от местных сопротивлений отдельные коэффициенты x складывают.

Гидравлический удар

Если при течении жидкости в трубопроводе быстро закрыть проходное сечение с помощью задвижки или другого аппарата, то произойдет резкое повышение давления, называемое гидравлическим ударом. При этом кинетическая энергия движущегося потока жидкости перейдет в потенциальную энергию, и давление может во много раз превысить нормальное значение.

Повышение давления вычисляется по уравнению Н. Е. Жуковского:

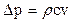где с – скорость распространения ударной волны, м/с (для жестких стенок трубы равна скорости звука в жидкости); v – начальная скорость жидкости в трубе (до момента перекрытия сечения), м/с.

Гидравлический удар может возникать во всех случаях быстрого перерыва подачи жидкости. Чтобы уменьшить вероятность его возникновения, увеличивают время закрытия задвижки (крана), при возможности уменьшают длину трубы, присоединяют к трубе дополнительные емкости в виде компенсаторов, гидроаккумуляторов.

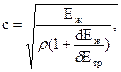При упругих стенках трубы скорость распространения ударной волны

где d - внутренний диаметр трубы, м; d - толщина стенок трубы, м; Ε_жи Ε_тр - модули упругости жидкости и материала трубы, Па.

Кавитация

При движении жидкости в сужающейся трубе, типа трубки Вентури, в наиболее узком сечении ее скорость достигает наибольшего значения, а давление будет минимальным. Предел уменьшения величины давления зависит прежде всего от того, что течет по трубопроводу: газ или капельная жидкость.

Кипение капельной жидкости (вода, спирт, масло и др.) при заданной температуре может быть получено понижением давления. Давление, при котором происходит кипение жидкости, называется давлением парообразования р_к.

Величину давления парообразования р_к для различных жидкостей можно найти в физических справочниках. В качестве примера приведем величину р_к для воды:

t , °C ............. 200 100 40 20 4

р_к, мм. рт. Cm ........ 11660 760 55,3 17 4

Из приведенных данных видно, что при температуре 20° С вода закипает при давлении 17 мм рт. ст. Если давление в наиболее узком сечении трубопровода достигнет давления парообразования, то жидкость в этом месте начнет кипеть и в трубе при этом образуются полости, заполненные паром, — каверны.

Закипание жидкости при пониженном давлении, возникающем в результате возрастания скорости потока, и образование в текущей жидкости полостей, заполненных паром или газом приводит к кавитации.

Кавитация может происходить во всех капельных жидкостях, в том числе и в жидких металлах. Последнее иногда наблюдается при использовании жидких металлов в качестве теплоносителей на атомных электростанциях.

Если после наиболее узкого сечения, в котором происходит кавитация, последует расширение трубы, то основная масса жидкости на этом участке будет двигаться в виде свободной струи, окруженной пенообразной смесью пузырьков пара и жидкости. Далее, ниже по течению, в некоторой точке паровая зона замкнется на стенке, и поток жидкости заполнит все сечение трубы.

Кавитация возникает не только при движении жидкости в трубопроводах, но и при внешнем обтекании тел, в частности, на ло-пастях гребных винтов, рабочих колес гидравлических турбин и насосов. Желательное увеличение скоростей вращения рабочих колес насосов, гидравлических турбин приводит к тому, что скорости становятся настолько большими, что в некоторой области давление падает до давления парообразования, и возникает кавитация.

Появление кавитации всегда вызывает увеличение сопротивления, т, е. добавочную потерю энергии. Кроме этого, она приводит к разрушению металла и появлению кавитационных шумов. Последствия кавитации настолько существенны, что обычно при проектировании насосов, турбин и винтов лопасти рассчитывают так, чтобы на них не возникала кавитация.

В качестве критерия, определяющего кавитационные свойства профилей, применяют число кавитации

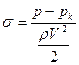
где р и V — соответственно давление и скорость в набегающем потоке.

Улучшение кавитационных свойств лопастей, т. е. уменьшение кавитационного числа, является одной из важнейших задач конструкторских бюро по проектированию насосов, турбин и винтов. Очевидно, что на лопастях кавитация возникает в точках, где давление наименьшее, а следовательно, скорость наибольшая. На рис. 3.14, а показана область возникновения кавитации на профиле крыла [5]. Кавитационная коррозия металла обычно происходит в местах, где кавитационная каверна замыкается. Природа разрушения металла еще недостаточно изучена, но можно утверждать, что разрушение происходит под действием очень мощных механических ударов пузырьков пара и жидкости, химического воздействия богатого кислородом воздуха, содержащегося в воде, и, как утверждают некоторые авторы, электрических полей, возникающих в каверне.

В результате всего этого воздействия почти все металлы разъедаются, их поверхность приобретает губчатый вид, и лопасти ломаются. Иногда процесс разрушения и поломки лопастей происходит очень быстро.

Шумы, возникающие при появлении кавитации, настолько велики, что они могут служить причиной вибрации отдельных элементов машин, приводящих к неустойчивой работе их и даже разрушению.

На рис. 3.14, б показан так называемый суперкавитирующий профиль лопатки корабельного винта. У таких винтов область кавитации не замыкается на поверхности лопасти, а уходит в бесконечность. Поэтому они не подвергаются интенсивной кави-тационной коррозии. Суперкавитирующие винты применяются на некоторых быстроходных судах.

Если нарушается сплошность потока жидкости, то возникает кавитация. Дело в том, что испарение жидкости происходит как непосредственно с ее поверхности, так и путем образования во всем ее объеме пара в виде пузырьков, которые затем разрушаются (конденсируются) при попадании в зону повышенного давления. Это вызывает появление микропустот, т. е. нарушение сплошности жидкости.

Таким образом, кавитация – это свойство движущейся жидкости образовывать паровоздушные пузыри с последующим их разрушением.

Кавитация часто возникает во всасывающих гидролиниях в результате местного уменьшения давления ниже критического значения (оно приблизительно равно давлению насыщенного пара этой жидкости при данной температуре). Она сопровождается гидравлическими микроударами и, как следствие, большим местным повышением температуры и давления, что вызывает разрушение деталей, появление вибраций, снижение КПД и др.

С кавитацией борются также, уменьшая разрежение в зонах ее возможного появления, в частности путем повышения давления. При этом применяют подпор во всасывающей линии насоса, а также эластичные специальные разделители сред в баках насосных установок. Используют материалы, стойкие против кавитационного разрушения, – бронзу, титан, коррозионно-стойкую сталь, повышая чистоту их обработки.

История развития науки

ОСНОВНЫЕ ПОЛОЖЕНИЯ ГИДРОМЕХАНИКИ

ГОСТ 17216—71 устанавливает 19 классов чистоты жидкостей, которые отличаются друг от друга количеством и размерами находящихся в жидкости частиц загрязнения. При этом наличие в жидкости частиц размером более 200 мкм (не считая волокон) не допускается.

Зависимость класса чистоты жидкостей от числа частиц загрязнителя

Класс чистоты жидкости	Число частиц загрязнителя в (100 ± 0,5) см³ жидкости при размере частиц, мкм, не более									Масса загрязнителей, %, не более
Класс чистоты жидкости	от 0,5 до 1	св. 1 до 2	св. 2 до 5	св. 5 до 10	св. 10 до 25	св. 25 до 50	св. 50 до 100	св. 100 до 200	волокна	Масса загрязнителей, %, не более
00	800	400	32	8	4	1	Отсутствие	АО	АО	Не нормируется
0	1600	800	63	16	8	2		Отсутствие	АО
1		1600	125	32	16	3			Отсутствие
2			250	63	32	4	1
3	Не нормируется			125	63	8	2
4				250	125	12	3
5				500	250	25	4	1
6				1000	500	50	6	2	1	0 ,000032
7				2000	1000	100	12	4	2	0 ,000064
8				4000	2000	200	25	6	3	0 ,000125
9				8000	4000	400	50	12	4	0,00025
10				16000	8000	800	100	25	5	0 ,0005
11				31500	16000	1600	200	50	10	0 ,001
12				63000	31500	3150	400	100	20	0 ,002
13					63000	6300	800	200	40	0 ,004
14					125000	12500	1600	400	80	0 ,008
15						25000	3150	800	160	0 ,016
16						50000	6300	1600	315	0 ,032
17							12500	3150	630	0 ,064

Для гидроприводов промышленных роботов удовлетворительным является использование рабочей жидкости от 7 до 12-го классов чистоты, в которых присутствуют механические частицы размером 10...25 мкм. Такая чистота в процессе эксплуатации обеспечивается применением специальных средств очистки, например фильтров.

Полученное пятно сравнивают с пятнами таблицы и «Шкалой образцов капельной пробы», которая кроме рисунков образцов содержит пояснения в форме таблицы (см. шкалу образцов кап. пробы). Оценка от 1 до 3 балла — показатель очень хороший; от 3 до 5 баллов — хорошо; от 5 до 7 — посредственно; от 7 до 8 — плохо; 8, 9 -очень плохо и масло подлежит замене.

Эталоны масляных капель

Дата: 2018-11-18, просмотров: 587.

12 3 4 5 6 7 8 9 Следующая ⇒