Вытеснение бронзы железом связано со смутным временем переселений и войн, переворотом в военном деле и ускорением роста экономики благодаря удешевлению средств производства.

В древней Греции сложились основные типы мировоззрений, действовали различные естественнонаучные школы. Ведущее место последовательно занимали:

Ионийская (6-7 в. до н.э);

Пифагорейская (6-5 в. до н.э);

Афинская (со второй половины 5 в до нашей эры).

Современная математика родилась в атмосфере ионийского рационализма. Математика ставила не только восточный вопрос «Как?», но и современный научный вопрос «Почему?» (Фалес – «отец» греческой математики). Математика помогла найти порядок в хаосе, связать идеи в логические цепочки, обнаружить основные принципы.

Математика была наиболее теоретической (отвлеченной от реальности) среди других наук. Одна из причин создания математических теорий – открытие иррациональности. Древним грекам стало известно логически строгое доказательство иррациональности 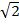, путем сведения к противоречию.

Доказательство

Предположим противное: пусть 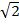 – рациональное число, значит  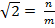, n – целое, m – натуральное.

,

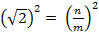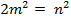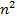à  – четное

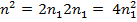
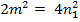
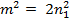
à 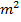 – четное,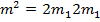

 – сократима, т.к. предполагалось, что  – рациональное число (несократимая дробь). Получаем противоречие.

Значит предположение не верно, 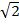 не является рациональным числом, т.е.  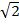– иррациональное.

Затем были открыты многие другие иррациональности (Архип, Теодор). Была приведена классификация иррациональностей.

В обстановке политической борьбы философы и наставники излагали свои теории, а заодно и новую математику. Впервые в истории группа критически мыслящих ученых (софистов) стала рассматривать проблемы математического характера скорее с целью уяснения их сути, чем ради пользы.

От этого периода дошел лишь один целый математический фрагмент (Гиппократ из Хиоса). Были исследованы площади плоских фигур, ограниченных как прямыми линиями, так и дугами окружностей, работал с прямоугольными треугольниками в стиле евклидовой геометрии. В это время ставились следующие задачи: 1) квадратура круга (нахождение такого квадрата, площадь которого была бы равна площади данного круга); 2) удвоение куба (определение ребра такого куба, который бы имел объем вдвое больше заданного куба – делийская задача); 3) трисекция угла (разделение любого заданного угла на 3 части). Эти проблемы нельзя точно решать геометрически с помощью конечного числа построений прямых линий и окружностей, это можно сделать только приближенно.

В связи с этими проблемами были открыты конические сечения, некоторые кривые 3, 4 порядка, преобразования параллелепипедов в куб, 1837 г. – доказательство Венцеля, что кубические иррациональности не принадлежат ни полю рациональных чисел, ни его расширению посредством присоединения квадратичных иррациональностей.

От группы софистов отмежевалась другая группа философов с математическими интересами – пифагорейцы. Софисты в большинстве подчеркивали реальность изменений, пифагорейцы стремились найти в природе и обществе неизменное. В поисках вечных законов Вселенной они изучали геометрию, арифметику, астрономию и музыку (Архит из Тарента). Пифагорейцы разбивали числа на классы: четные/нечетные, простые/составные, треугольные/квадратные и другие.

Пифагорейцы исследовали свойства чисел, привнесли числовой мистицизм и сделали числа основой своей философии о вселенной, пытаясь свести все соотношения к числовым» («все есть число»). Пифагорейцам были известны некоторые свойства правильных многоугольников и многогранников. Наиболее важным было открытие иррационального числа.    

Одна из концепций античной общей теории отношений связана с именем Евдокса (4 в. до н. э.):

1. Если а = b и с = b, то а = с; а если а = b, то 2. a + с = c + b. 3. a - b = с - b. 4. Целое больше части

При построении математических теорий в античной Греции рано выделился специфический класс проблем, для решения которых оказалось необходимым исследовать предельные переходы, бесконечные процессы, непрерывность и т. п.

Ярким примером ученых, которые искали выход из этих затруднений, являлся Демокрит (4 в. до н.э.): все тела состоят из малых атомов. Тела различаются между собой по способу соединения в них атомов.

Противопоставления атомическим философским воззрениям Демокрита являются логические парадоксы (апории Зенона):

дихотомия – невозможность осуществить движение, так как путь может быть делим до бесконечности (пополам, еще раз пополам и т. д.) и поэтому надо последовательно преодолевать бесконечное множество участков пути;

Ахиллес, который не может догнать черепаху, так как ему надо последовательно достигать тех мест, где только что находилась черепаха, т. е. исчерпывать бесконечную последовательность отрезков пути;

Апории Зенона убедительно показали, что точные доказательства нельзя вести, опираясь на понятие бесконечностей.

В античной математике процесс систематизации и обобщения дал значительные результаты.