Математика Древнего Египта

Познания математики основаны главным образом на 2 больших папирусах (математический папирус Ринда (5,5 м * 0,32 м), второй папирус находится в Москве (5,5 м * 8 см)), содержащиеся в них сведения относятся к 2000 г. до н.э.. папирусы содержат задачи прикладного характера. При их решении производят действия с дробями, вычисляют площади прямоугольника, треугольника, трапеции и круга, объем цилиндра, размеры пирамид. При решении одной задачи находят сумму геометрической прогрессии, в другой – объем усеченной пирамиды с квадратным основанием. Отличительной чертой египетской арифметики являются действия с дробями. Все дроби сводятся к сумме основных (аликвотных) дробей вида . Например,

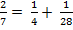
Многие задачи сводились к линейному уравнению с одним неизвестным. Неизвестное обозначали в виде кучи («хау»). Пример: некое количество, его 2/3, его ½, его 1/7, сложенные вместе дают 33. Какого их количество?

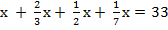à 97 х = 33*42 à х =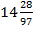

В большинстве задач речь идет о количестве хлеба, хранении зерна и т.д.

Математика древнего Вавилона

Название Древний Вавилон распространяют на совокупность государств, располагавшихся в междуречьях Тигра и Евфрата и существовавших в период от 2000 до 200 г.г. до н.э.

В вавилонской системе математических символов есть 2 основных элемента: клин = 1, крючок = 10. Писали на глиняных табличках, поэтому символы простые. Использовалась шестнадцатеричная система (время, градусы).

Первая вавилонская династия Хаммураки (1950 г. до н.э.) хорошо развита алгебра. Умели решать линейные, квадратные, биквадратные уравнения в отличии от египтян, умеющих решать только линейные уравнения. Встречаются задачи измерения углов, найдено приближенное значение числа π = 3. Объем усеченной пирамиды найден не был.

Развитие математики в Древней Азии

Математика Древнего Китая

По утверждению китайского историка Ли Яня математические познания китайцев восходят к 14 в. до н.э. Есть сведения о десятичной системе счета, об оперировании большими числами, циркулем, линейкой.

Самым ранним математическим сочинением является «Математика в 9 книгах» (начало нашей эры)

Книга «Измерение полей» посвящена площади прямолинейных фигур, круга, сектора, кольца (π = 3). Другая книга посвящена пропорциональному делению. Третья – правилам суммирования арифметических прогрессий. Четвертая – нахождению элементов геометрических фигур по заданной площади и другим элементам. Пятая «Строительство крепостных стен. Практические расчеты». Шестая – «Задачи о пропорциональном распределении налогов, задачи на совместную работу». Седьмая – задачи, сводившиеся к линейным уравнениям и их системам. Восьмая – решение систем линейных уравнений с большим числом неизвестных (n = 5). Девятая – задачи определения недоступных расстояний и высот с помощью теорем Пифагора и свойств подобных треугольников.

Китайские ученые ввели отрицательные числа, занимались магическими квадратами

4 9 2

3 5 7

8 1 6

Наряду с математическими, решались комбинаторные задачи.

Математика Древней Индии

Древние и средневековые математики народов Индии имели много общего с китайской математикой, но с учетом феодальной системы организации общества, кастовым расслоением населения, математика в Индии развивалась медленно. Трудились ученые Ариабхата, Брахмудта. Их математические сочинения в стихах содержали … арифметики, геометрии, тригонометрии. Индийские математики правильно трактовали понятие отрицательного числа: + имущество, – долг. Равное имущество + равные долг вводит понятие нуля.

sinvers = 1 – cos .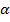

При этом всегда происхождение математики исходило из практической деятельности людей.

29.09.2018