Для анализа (4.6) применим известные из курса тригонометрии формулы преобразования:

     .

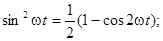
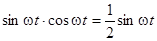Применяя их к (4.6) получим:

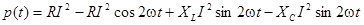,     (4.7)

где I - действующее значение тока, причем  .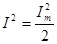

Первые два слагаемые в (4.7) определяют мгновенную мощность, выделяемую на элементе R. Можно записать, что

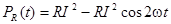                    (4.8)

Как видно из (4.8) мгновенная мощность p_R(t) содержит постоянную составляющую Р = RI² и переменную, меняющуюся с удвоенной частотой. График р_R(t) приведен на рис. 4.1. График наглядно показывает, что мощность р_R(t) всегда положительна и изменяется от 0 ( в момент t=0, k×T/2) до 2RI² ( в моменты (2k-1)× T/4), Т=2p/w - период тока.

Среднее за период значение мощности обозначают Р и называют активной мощностью, причем

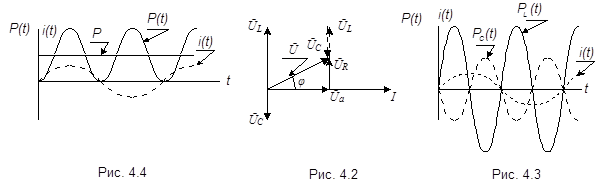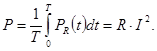                                    (4.9)

Для более детального анализа мгновенной мощности Р_R(t) обратимся к выражению (4.5),. Этому выражению соответствует векторная диаграмма рис.4.2. В ней в качестве исходного принят вектор тока 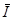. Вектор напряжения на индуктивности 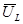опережает ток, а на емкости  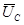отстает от тока на 90^о. Напряжение на резисторе  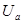совпадает по фазе с током.

Проведем сложение векторов. Для этого начало вектора 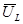 переместим в точку конца вектора 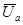, а начало вектора  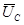- в точку конца вектора 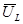. Результатом сложения является вектор  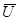выходящий из начала вектора  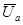в конец вектора 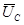. Угол j определяет сдвиг фаз между током и результирующим напряжением, т.е.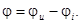

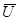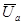Соединим точки концов двух векторов -  и . Обозначим вновь полученный вектор  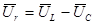 . Образовавшийся треугольник из векторов 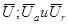называют треугольником напряжений. Для него справедливы следующие выражения:

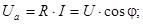
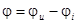                      (4.10)

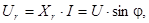
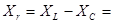
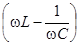                            (4.11)

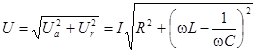                                                   (4.12)

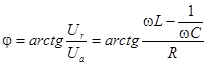                                                                 (4.13)

Возвратимся вновь к анализу мгновенной мощности, выделяемой на элементе R - p_R(t). С учетом (4.10) перепишем (4.8) в виде

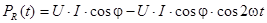                                                   (4.14)

Первое слагаемое в правой части полностью соответствует (4.9) т.е. определяет активную мощность

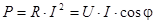                                         [Вт]                          (4.15)

Выражение (4.15) используется в практике намного чаще так как определяет зависимость активной мощности от сдвига фаз между действующими значениями тока и напряжения цепи. В силу этого коэффициент cos j называют коэффициентом мощности и обозначают l

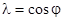                              (4.16)

Обратимся к исходному выражению для мгновенной мощности цепи - (4.7). В нем третье и четвертое слагаемое определяют мощность, выделяемую на реактивных элементах - индуктивности

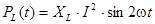                           (4.17)

и емкости

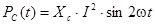                           (4.18)

Каждое из этих слагаемых изменяются с удвоенной (относительно тока) частотой, но имеют противоположные фазы (рис.4.3). Так как постоянная составляющая в (4.17) и (4.18) отсутствуют, то среднее значение каждого из них равна нулю. Однако сумма p_L(t) и p_C(t) отлична от нуля и определяет мгновенную мощность реактивных элементов (участков) цепи. Определим ее:

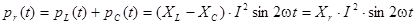               (4.19)

Применим к (4.19), (4.11), тогда

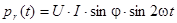               (4.20)

Коэффициент

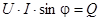     [вар]             (4.21)                                                                               

называется реактивной мощностью, обозначается Q и измеряется в воль-амперах реактивных [вар].

Теперь общее выражение для мгновенной мощности всей цепи (рис.3.1) можно записать в виде

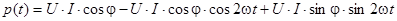                   (4.22)

Второе и третье слагаемые в (4.22) свернем как косинус суммы аргументов - 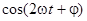. Тогда

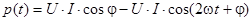                                                      (4.23)

Таким образом, мгновенная мощность цепи постоянную и переменную составляющие. Переменная составляющая изменяется относительно постоянной с удвоенной частотой (рис.4.4). Амплитудное значение переменной составляющей обозначают S и называют полной мощностью цепи

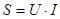[ВА]           (4.24)

Полная мощность в 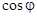 раз превышает постоянную составляющую (активную мощность). Поэтому график мгновенной мощности заходит в область отрицательных значений. Величина области отрицательных значений

определяется коэффициентом мощности. Физически эта область определяет моменты времени в которые цепь возвращает энергию источника.

Если умножить все стороны треугольника сопротивлений (рис.3.2) на 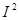, то получим треугольник мощностей (рис.4.5). В этом треугольнике гипотенуза - полная мощность S, прилежащей к острому углу катет - активная мощность Р, а противолежащий - реактивная мощность Q. Угол  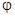определяется сдвигом фаз между током и напряжением цепи и задает значение коэффициента мощности. Для треугольника очевидны выражения

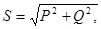                     (4.25)

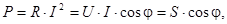
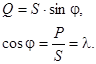                                                                                                 (4.26)

Полная мощность S это теоретически достижимая, расчетная мощность, По значению S производятся расчеты сечения проводов, изоляция, параметры приемников электрической энергии. Из-за сдвига фаз 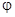 мощность полностью не реализуется. Поэтому  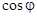и получил название коэффициента мощности. Всегда стремятся обеспечить его высоким.