ЛЕКЦИЯ 1.1.
Закон Ома и Кирхгофа
Все электрические цепи подчиняются законам Ома и Кирхгофа. Краткая информация об этих законах заключается в следующем.
Закон Ома для участка цепи без ЭДС устанавливает связь между током и напряжением на этом участке
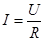или 
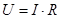(1.14)
Закон Ома для участка цепи, содержащего ЭДС позволяет найти ток этого участка
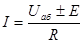(1.15)
здесь а, б - крайние точки участка; Е - значение ЭДС.
В (1.15) знак «плюс» ставится при совпадении тока, протекающего по участку, с направлением ЭДС.
Первый закон Кирхгофа имеет две формулировки.
1. Сумма токов протекающих через любой узел равна нулю.
2. Сумма токов втекающих в узел равна сумме токов вытекающих из него.
Второй закон Кирхгофа:
Алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль этого контура, т.е.
åIR = åE.
В каждую из сумм слагаемые входят со знаком «плюс», если они совпадают с направлением обхода.
ЛЕКЦИЯ 1.2
СИНУСОИДАЛЬНЫЙ ТОК. ФОРМЫ ЕГО ПРЕДСТАВЛЕНИЯ.
В практике электротехники в качестве переменного тока широкое применение нашел ток синусоидальной формы. Это обусловлено рядом преимуществ:
-генераторы синусоидального тока значительно дешевле в производстве, чем генераторы постоянного тока;
-переменный ток легко преобразуется в постоянный;
-трансформация и передача электрической энергии переменным током экономичнее чем постоянным;
-двигатели переменного тока имеют простую конструкцию, высокую надежность и невысокую стоимость.
В настоящее время переменный ток применяется в промышленном приводе и в электроосвещении, в сельском хозяйстве и на транспорте, в технике связи и в быту. Производство электрической энергии также осуществляется на переменном токе. Огромную роль в деле внедрения переменного тока сыграли русские ученые П.Н.Яблочков и М.О.Доливо-Добровольский.
ЛЕКЦИЯ 1.3.
КОМПЛЕКСНЫЕ СОПРОТИВЛЕНИЯ И ПРОВОДИМОСТИ ЭЛЕМЕНТОВ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Комплексное сопротивление
Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме - Z.
Хороши известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то
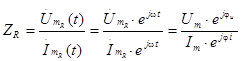
Но на предыдущей лекции было установлено, что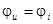 
. Поэтому
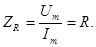(3.1)
Таким образом видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между токами и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.
Комплексное сопротивление емкости определяется отношением
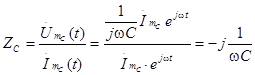. (3.2)
Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90о. Это хорошо согласуется с ее максимальным значением
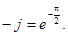
Поэтому на емкости напряжение отстает от тока на 90о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.
Коэффициент 1/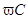 
определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХС, т.е.
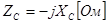. (3.3)
Комплексное сопротивление индуктивности определяется отношением
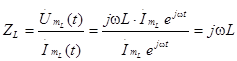. (3.4)
И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90о.
Коэффициент wL определяет величину сопротивления в Омах. Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.
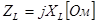. (3.5)
Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность - реактивными элементами цепи.
Определим теперь комплексное сопротивление электрической цепи, содержащей активные и реактивне элементы, например последовательно включенные R, L и С элементы (рис.3.1). Такая цепь представляет замкнутый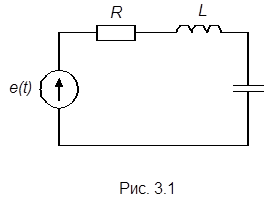 
контур, поэтому для нее справедлив второй закон Кирхгофа
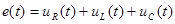. (3.6)
В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 1.2. Такой прием получил название символического метода. Так как ток протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду
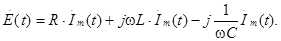
Преобразуем это выражение к виду
.
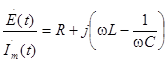По определению выражение в правой части последнего равенства есть ни что иное, как комплексное сопротивление цепи рис.3.1, т.е.
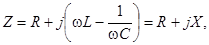(3.7)
где R - действительная часть или активное сопротивление цепи.
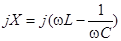- мнимая часть или реактивное сопротивление цепи.
Выражение (3.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится понятие треугольника сопротивления (рис.3.2).
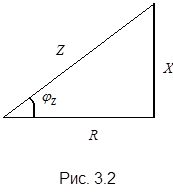В треугольнике - гипотенуза определяется модулем комплексного сопротивления Z, причем
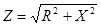(3.8)
Противолежащий катет - реактивным сопротивлением X, причем
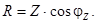(3.9)
Угол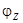 
определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи, причем
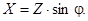(3.10)
Учитывая выражения (3.8) ¸ (3.11) легко перейти от алгебраической к тригонометрической форме комплексного сопротивления
Z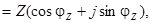 
(3.12)
a применив формулу Эйлера получить показательную форму
Z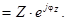 
(3.13)
Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении
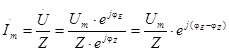(3.14)
Выражение (3.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение
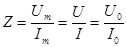. (3.15)
Комплексна проводимость
В цепях постоянного тока проводимость резистора определяется отношением тока к напряжению:
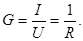
Эта величина обратно пропорциональна сопротивлению.
В цепях переменного тока следует пользоваться понятием комплексной проводимости, которая обозначается Y и, в общем случае, содержит действительную G и мнимую В части:
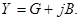
Как и в цепях постоянного тока комплексная проводимость участка цепи обратна комплексному сопротивлению, т.е.
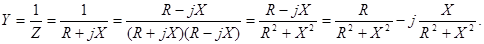
Отсюда
, 
, 
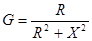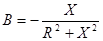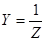, (3.16)
где Y - модуль комплексной проводимости.
Соотношение между составляющими комплексной проводимости аналогичны соотношениям между составляющими комплексного сопротивления.
Комплексная проводимость резистора
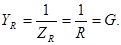(3.17)
Комплексная проводимость конденсатора
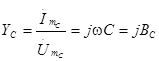. (3.18)
Комплексная проводимость индуктивности
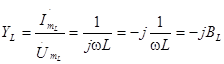. (3.19)
В заключение отмети, что комплексное сопротивление удобно применять для анализа участков электрической цепи с последовательным включением элементов, а комплексную проводимость - для участков с параллельным включением элементов.
ЛЕКЦИЯ 1.4.
Применим к (4.19), (4.11), тогда
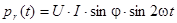(4.20)
Коэффициент
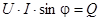[вар] (4.21)
называется реактивной мощностью, обозначается Q и измеряется в воль-амперах реактивных [вар].
Теперь общее выражение для мгновенной мощности всей цепи (рис.3.1) можно записать в виде
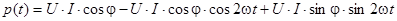(4.22)
Второе и третье слагаемые в (4.22) свернем как косинус суммы аргументов -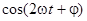 
. Тогда
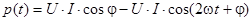(4.23)
Таким образом, мгновенная мощность цепи постоянную и переменную составляющие. Переменная составляющая изменяется относительно постоянной с удвоенной частотой (рис.4.4). Амплитудное значение переменной составляющей обозначают S и называют полной мощностью цепи
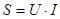[ВА] (4.24)
Полная мощность в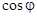 
раз превышает постоянную составляющую (активную мощность). Поэтому график мгновенной мощности заходит в область отрицательных значений. Величина области отрицательных значений
определяется коэффициентом мощности. Физически эта область определяет моменты времени в которые цепь 
возвращает энергию источника.
Если умножить все стороны треугольника сопротивлений (рис.3.2) на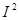 
, то получим треугольник мощностей (рис.4.5). В этом треугольнике гипотенуза - полная мощность S, прилежащей к острому углу катет - активная мощность Р, а противолежащий - реактивная мощность Q. Угол 
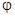определяется сдвигом фаз между током и напряжением цепи и задает значение коэффициента мощности. Для треугольника очевидны выражения
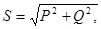(4.25)
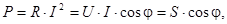
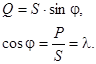(4.26)
Полная мощность S это теоретически достижимая, расчетная мощность, По значению S производятся расчеты сечения проводов, изоляция, параметры приемников электрической энергии. Из-за сдвига фаз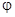 
мощность полностью не реализуется. Поэтому 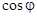и получил название коэффициента мощности. Всегда стремятся обеспечить его высоким.
Резонанс токов
Резонанс токов возникает в цепи с параллельным включением элементов (рис.5.1). Такая цепь содержит два сложных потенциальных узла, а все элементы находятся под одним и тем же напряжением
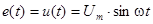(5.1)
Для любого из узлов - 1 или 1’ справедлив первый закон Кирхгофа:
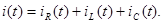(5.2)
Применяя к (5.2) выражения (1.7) и (1.12) приведем его к виду
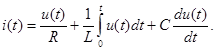(5.3)
Подставим в (5.3) вместо u(t) его значение из (5.1) и решим его
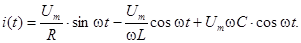(5.4)
Векторная диаграмма, построенная по (5.4) приведена на рис. 5.2. В качестве исходного в ней принят общий для всех элементов цепи вектор напряжения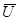 
. С этим вектором совпадает по направлению вектор тока через резистор. Его величина равна
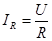
Вектор тока через индуктивность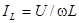 
отстает от вектора напряжения, а вектор тока через емкость опережает его на 90о. Проведем последовательное сложение векторов 
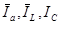. Результатом сложения является вектор 
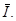Он сдвинут по фазе относительно вектора 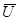на угол j. Разность векторов 
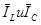дает вектор реактивного тока 
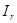. Его величина
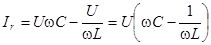(5.5)
Векторы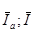 
и 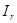образуют треугольник токов. Для этого треугольника справедливы выражения
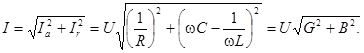(5.6)
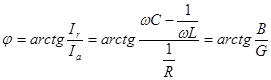(5.7)
Треугольник токов наглядно показывает, что для достижения резонанса в цепи необходимо обеспечить равенства противофазных токов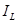 
и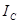 
. Тогда результирующий реактивный ток цепи 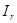и угол j будут равны нулю, а сопротивление цепи станет активным. Из выражения (5.5) видно что 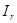может быть равно нулю при соблюдении условия
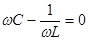(5.8)
Отсюда легко определить:
-частоту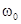 
, на которой наступает резонанс (резонансную частоту) при заданных значениях элементов L и С
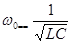; (5.9)
-значение одного из элементов L или С, если заданы резонансная частота 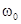и другой элемент
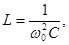
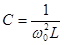. (5.10)
Определим значение тока всей цепи и токов, протекающих в ее ветвях в режиме резонанса.
Действующее значение тока всей цепи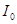 
на частоте 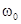легко найти по (5.6)
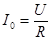(5.11)
Но это значение равно току, протекающему через активное сопротивление цепи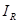 
т.е.
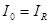(5.12)
Ток, протекающий через элемент L определим по закону Ома
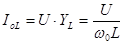. (5.13)
Подставляя в (5.13) вместо U его значение из (5.11) получим
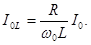(5.14)
Аналогично определяем выражение для тока через элемент
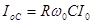(5.15)
Принимая во внимание (5.8) нетрудно сделать вывод о том, что токи протекающие через индуктивный и емкостной элементы равны по величине, но противоположны по фазе. Величина Q равная
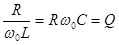(5.16)
может быть больше единицы, в специальных устройствах достигает несколько десятков и сотен единиц и называется добротностью.
Еще раз подчеркнем замечательную особенность цепи в режиме резонанса. Токи протекающие в ветвях реактивных элементов могут принимать значения в десятки и сотни раз больше общего тока цепи. Поэтому резонанс цепи называют резонансом токов. Очень важно и то, что они противофазны. Именно это указывает на то, что в цепи происходит колебательный процесс с частотой 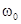по передаче электрической энергии конденсатора в магнитную энергию индуктивности и наоборот. Энергия источника на этот процесс не затрачивается (при идеальных L и С). Она расходуется только на преодоление сопротивления резистора R. Поэтому цепь рис.5.1. называют параллельным колебательным контуром.
Чтобы завершить анализ цепи рассмотрим зависимость ее токов и напряжения от частоты (рис.5.4). Ток, протекающий через элемент R - iR определяется законом Ома и не зависит от частоты. Ток через емкость ic согласно (5.15) прямопропорционален частоте, а ток через индуктивность iL -обратнопропорционален. На частоте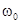 
они равны по величине, но противоположны по направлению. Общий ток цепи определяется суммой трех токов. Поэтому он имеет большое значение на частотах, дальних от резонансной, но принимает значение iR на резонансной частоте. Физически это означает что на резонансной частоте проводимость цепи минимальна (она равна проводимости только элемента R). Поэтому падение напряжения между узлами 1-1’ максимально на частоте 
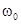и имеет вид резонансной прямой. В силу этих качеств параллельный колебательный контур широко применяют в радио и радиотехнических устройствах для выделения сигналов на заданной частоте.
 |
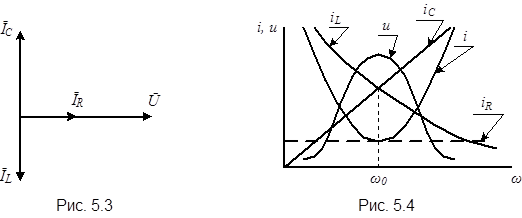Резонанс напряжений
 |
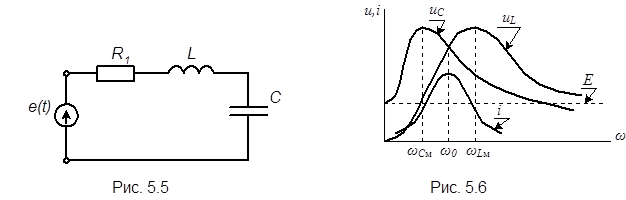Резонанс напряжений возникает в цепи с последовательным включением элементов (рис.5.5)
Известно, что комплексное сопротивление токов цепи определяется выражением.
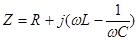
По определению резонанс в цепи рис.5.5 наступает когда выполнится условие
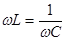
Отсюда видно, что резонанс в цепи возникает на частоте
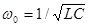
Очевидно также, что
, 
.
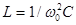Видим, что полученные выражения полностью соответствуют (5.9) и (5.10). Это подтверждает единство физической сути различных видов резонанса.
Определим ток и напряжение всей цепи , а также падение напряжения на ее отдельных элементах в режиме резонанса.
Так как сопротивление всей цепи в режиме резонанса минимально и равно R то ток в ней максимален и равен
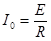, (5.17)
а падение напряжения определяется ЭДС источника - Е.
Падение напряжения на отдельных элементах легко найти по закону Ома. Так, падение напряжения на резисторе R равно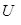 
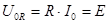(5.18)
Тривиальный математически результат интересен по физической сути. Все напряжение источника выделяется на одном элементе цепи.
Падение напряжения на индуктивности равно
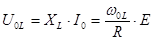(5.19)
Величина
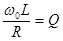(5.20)
называется добротностью и может принимать значение десятков и сотен единиц. Значит, падение напряжения на индуктивности может в десятки и сотни раз превышать ЭДС источника.
Падение напряжения на емкости равно
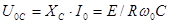(5.21)
Так как 
, то падение напряжения на емкости равно по величине падению напряжения на индуктивности, но согласно (5.8) они противоположны по знаку. Отношение напряжения на индуктивности или на емкости в режиме резонанса к току в этом режиме называют характеристическим сопротивлением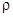 
, причем
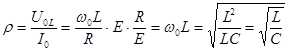(5.22)
В силу того что
,
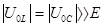рассматриваемый режим назван резонансом напряжений. Противофазность напряжени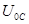й 
и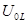 
указывает на то, что в цепи происходит такой же колебательный процесс с частотой 
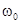, как и в параллельном колебательном контуре.
Здесь также энергия источника затрачивается только на преодоление сопротивления резистора R. Поэтому цепь называется последовательным колебательным контуром.
Завершим анализ резонанса напряжений разбором частотной зависимости тока цепи рис.5.5. и падений напряжений на элементах L и С от частоты (рис.5.6). На рисунке пунктиром отмечен график ЭДС. Падение напряжения на идеальной индуктивности при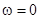 
равно нулю. С увеличением частоты сопротивление индуктивности, а значит и падение напряжения на ней увеличивается. Когда частота устремляется в бесконечность сопротивление ХL также устремляется в бесконечность. При этом падение напряжения стремится к Е. Между крайними точками существует экстремум напряжения 
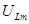который находится по формуле
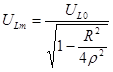(5.23)
Частота, на которой достигается этот максимум определяется выражением
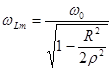(5.24)
Сопротивление емкости на частоте 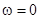равно бесконечности и значит напряжение на ее обкладках равно Е. С увеличением частоты сопротивление ХС уменьшается, а при 
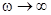стремится к нулю. Между крайними точками также существует экстремум причем
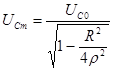(5.25)
Частота, на которой достигается этот максимум определяется выражением
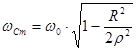(5.26)
Так как подкоренное выражение в (5.24) и (5.26) всегда меньше единицы то очевидно, что
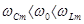
Кроме того
.
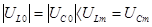В силу этих особенностей единственным верным признаком наступления резонанса в цепи является максимум тока, значение которого изменяется с изменением частоты по резонансной кривой.
ЛЕКЦИЯ 1.1.
ЭЛЕМЕНТЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
1.Предмет и задачи дисциплины. Построение курса. Методика работы над учебным материалом.
Электротехника - область науки и техники, использующей электрическое и магнитное явления для практических целей. История развития этой науки занимает два столетия. Она началась после изобретения первого электрохимического источника электрической энергии в 1799 г. Именно тогда началось изучение свойств электрического тока, были установлены основные законы электрических цепей, электрические и магнитные явления стали использоваться для практических целей, были разработаны первые конструкции электрических машин и приборов. Жизнь современного человека без использования электрической энергии немыслима.
Большой вклад в развитие электротехники внесли русские ученые. Так еще в 1802 г. Выдающийся русский ученый В.В. Петров впервые указал на возможность использования электрической дуги для освещения. Было разработано большое число конструкций дуговых ламп освещения. Но наиболее экономичной оказалась электрическая свеча П.Н. Яблочкова (1876г). В предложенной Яблочковым конструкции был впервые применен для практических целей трансформатор. Но главная заслуга изображения в том, что оно повысило спрос на генераторы переменного тока.
Все возрастающая потребность в использовании электрической энергии привело к проблеме ее централизованного производства, передачи на дальние расстояния, распределения и экономичного использования. Решение проблемы привело к разработке и созданию трехфазных электрических цепей. Огромная заслуга в создании элементов таких цепей принадлежит выдающемуся русскому ученому М.О. Доливо-Добровольскому. Он создал трехфазный асинхронный двигатель, трансформатор, разработал четырехпроводную и трехпроводную цепи (1891г.).
Сегодня электрическая энергия используется в технике связи, автоматике, измерительной технике, навигации. Она применяется для выполнения механической работы, нагрева, освещения, используется в технологических процессах (электролиз), в медицине, биологии, астрономии, геологии и др. Столь обширное проникновение электротехники в жизнь человека привело к необходимости включить ее в состав общетехнических дисциплин при подготовке специалистов всех технических специальностей. При этом перед студентами стоят две главные задачи. Первая задача - ознакомиться и усвоить физическую сущность электрических и магнитных явлений. Это позволит понять принципы работы электромагнитных устройств, правильно их эксплуатировать.
Однако, современному специалисту недостаточно знаний одних физических явлений. Поэтому студенты неэлектрических специальностей должны получить навыки в методах расчетов элементарных цепей и устройств, необходимых для успешного изучения последующих прикладных курсов.
Дисциплина «Электротехника и электроника» рассчитана на 80 (88) часов. Из них 40 часов - лекций, 20 часов - практических занятий, 20 (28) часов - лабораторных занятий. Она включает два раздела «Электротехника» и «Электроника», завершается КП, зачетом (экзаменом). Курс построен так, что каждая из 7 тем закрепляется практическими и лабораторными занятиями. Эти виды занятий сопровождаются текущим контролем, который положен в основу формирования рейтинга студента. Поэтому залогом успешного освоения дисциплины является систематическая работа над материалом.
Весь теоретический материал имеет строгое математическое обоснование. Он востребует знания студентов по математике ( разделы векторной алгебры, дифференциального, интегрального, комплексного исчисления, рядов), а также по физике (разделы электричества, магнетизма, молекулярной физики).
2. Общие понятия и определения линейных электрических цепей (ЛЭЦ).
Электротехническое устройство и происходящие в нем физические процессы в теории электротехники заменяют расчетным эквивалентом - электрической цепью.
Электрическая цепь - это совокупность соединенных друг с другом проводниками источников электрической энергии и нагрузок, по которым может протекать электрический ток. Электромагнитные процессы в электрической цепи можно описать с помощью понятий ток, напряжение, ЭДС, сопротивление, проводимость, индуктивность, емкость.
Электрический ток может быть постоянным и переменным. Постоянным называют ток, неизменный во времени. Он представляет направленное упорядоченное движение носителей электрического заряда. Как известно из курса физики, носителями зарядов в металлах являются электроны, в полупроводниках электроны и дырки (ионы), в жидкостях - ионы.
Упорядоченное движение носителей зарядов в проводниках вызывается электрическим полем. Поле создается источниками электрической энергии. Источник преобразует химическую, механическую, кинематическую, световую или другую энергию в электрическую. Он характеризуется ЭДС и внутренним сопротивлением. ЭДС источника м.б. постоянной или переменной во времени. Переменная ЭДС может изменяться во времени по любому физически реализуемому закону. Ток, протекающий по цепи под воздействием переменной ЭДС также переменный.
Постоянный ток принято обозначать буквой I, переменный i(t); постоянную ЭДС - Е, переменную е(t), сопротивление - R, проводимость -g. В международной системе единиц (СИ) ток измеряют в амперах (А), ЭДС - в вольтах (В), сопротивление в омах (Ом), проводимость - в сименсах (См).
При анализе электрических цепей, как правило оценивают значение токов, напряжений и мощностей. В этом случае нет необходимости учитывать конкретное устройство различных нагрузок. Важно знать лишь их сопротивление - R, индуктивность - L, или емкость - С. Такие элементы цепи называют приемниками электрической энергии.
Для включения и отключения элементов электрических цепей применяют коммутационную аппаратуру ( рубильники, выключатели, тумблеры (см. рис. 1.1.). Кроме этих элементов в электрическую цепь могут включаться электрические приборы для измерения тока, напряжения, мощности.
Изображение электрической цепи с помощью условных графических обозначений называют электрической схемой (рис. 1.2).
Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении принято называть вольтамперной характеристикой.
Приемники электрической энергии, вольтамперные характеристики которых являются прямыми линиями (рис. 1.3), называются линейными, а электрические цепи только с линейными элементами - линейными электрическими цепями.
Электрические цепи с нелинейными элементами называются нелинейными электрическими цепями.
Дата: 2018-11-18, просмотров: 486.
