Синтез вариантов систем на морфологических таблицах можно осуществлять с использованием качественных классификационных признаков, характеризующих свойства альтернатив. Классификационные признаки несут обобщенную специфическую информацию о системах, отличающуюся от рассмотренной ранее информации, определяющей предпочтения по критериям качества. Классификационные признаки могут Сыть использованы в задачах поиска в морфологических множествах вариантов, наиболее сходных по функциям и структуре с заданным известным прототипом или поисковым заданием, отражающим желаемые для исследователя свойства. В таких задачах исследователи и эксперты в большей степени оперируют не количественными данными, а понятиями, имеющими качественный характер. Качественные признаки наиболее информативны и при решении задач синтеза оригинальных (экзотичных) вариантов систем, обладающих свойствами существенной новизны и конкурентоспособности.

Синтез вариантов, сходных с прототипом. Задачу поиска в морфологическом множестве вариантов систем, наиболее близких к прототипу или поисковому заданию, можно решать на основе мер сходства и различия. Целевая функция в этой задаче имеет следующий вид: найти подмножество S Î W, для элементов которого

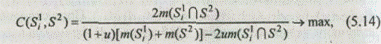
где С( S_i ¹ , S ² ) — мера сходства между описанием синтезированного варианта системы S_i ¹ и прототипом или поисковым решением S ².

Морфологический синтез на основе классификационных признаков с учетом целевой функции, в основе которой лежит мера сходства (5.14), осуществляется следующим образом.

Вначале формируется морфологическая таблица (табл. 5.16), в которой альтернативы A_ij охарактеризованы множеством признаков f_ij.

Наличие у альтернативы того или иного признака из указанного множества отмечается в морфологической таблице единицей, а отсутствие — нулем. Прототип, относительно которого вычисляется мера сходства, задается аналогичным образом. Предположим, что прототип синтезирован из альтернатив морфологической таблицы и состоит из композиции А₁₁А₂₁А₃₁. После определения прототипа осуществляется генерация всех вариантов, содержащихся в рассматриваемой таблице. Поисковые образы сгенерированных вариантов сравниваются с образом прототипа (табл. 5.17).

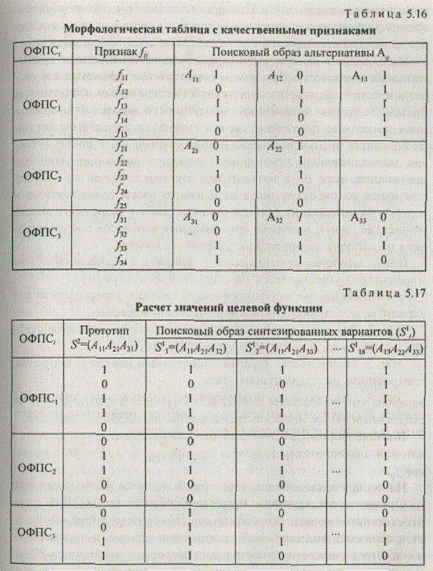
Для каждой пары, состоящей из прототипа и поискового образа варианта, вычисляется мера сходства: C ( S^l_l , S ² ) =0,87; C ( S^l ₂ , S ²) = 0,84; C ( S^l ₁₈ , S ² ) = 0,7. Варианты упорядочиваются по степени близости к прототипу. Подмножество наиболее близких к прототипу вариантов в конечном итоге предоставляется эксперту для более детального анализа.

Выявление в морфологических множествах наиболее оригинальных вариантов. Прогресс в социально-экономической и технологической сферах определяется внедрением новых эффективных систем. Задача по выявлению и обоснованию новых вариантов систем достаточно трудоемка, так как требует сопоставления систем по большому числу классификационных признаков. Вариант системы, принадлежащей некоторому множеству вариантов, наиболее оригинален, если он в наименьшей степени включен по составу признаков во все оставшиеся варианты из рассматриваемого множества. Формализация процедуры выявления в морфологическом множестве новых, наиболее оригинальных вариантов систем основана на использовании мер включения и сходства.

Поиск наиболее оригинального варианта в морфологическом множестве осуществляется но следующему алгоритму.

Этап 1. На основе морфологической таблицы генерируются все варианты, образующие морфологическое множество.

Этап 2. Для всего морфологического множества вариантов строится матрица включения или матрица сходства.

Этап 3. Вычисляется правый собственный вектор W матрицы, построенной на предыдущем этапе.

Этап 4. Отыскивается подмножество минимальных значений в векторе W, которому соответствуют наиболее оригинальные варианты. т.е. ищутся минимумы целевой функции:

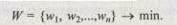
Число искомых элементов вектора п задается исследователем.