Многокритериальный синтез

Морфологический синтез рациональных вариантов по критериям качества начинается с независимой оценки альтернатив, принадлежащих соответствующим функциональным подсистемам. Метод основан на двух предположениях. Первое предположение заключается в том, что альтернативы, принадлежащие одним функциональным подсистемам, можно оценивать независимо от альтернатив, принадлежащих другим функциональным подсистемам. Второе предположение состоит в том, что наилучший целостный вариант системы содержит лучшие альтернативы. Для ряда сложных функциональных систем справедливо второе предположение.

Рассматриваемый подход используется для предварительного усечения исходного морфологического множества. Оставшееся после усечения обозримое подмножество рациональных вариантов исследуется на предмет оценки их эффективности и совместимости отдельных альтернатив.

Морфологический синтез рациональных вариантов может реализоваться по двум направлениям. Первое направление предусматривает поиск наиболее рациональных вариантов в самом морфологическом множестве. При этом максимизируется аддитивная или мультипликативная целевая функция.

Второе направление предполагает поиск в морфологическом множестве вариантов, наиболее сходных с поисковым заданием. Расчет значений целевых функций осуществляется для каждого варианта, синтезируемого на исследуемой морфологической таблице. Для этой цели используется специальный алгоритм генерации всех вариантов систем, содержащихся в морфологической таблице. Алгоритм функционирует по принципу лексикографического упорядочения объектов.

Общее число перебираемых компьютером вариантов определяется здесь декартовым произведением множеств альтернатив, относящихся к каждой функции обобщенной функциональной подсистемы.

Рассмотрим основные положения морфологического синтеза рациональных вариантов систем по множеству критериев на примере синтеза мероприятий для развития инфраструктуры города. Пусть задана морфологическая таблица (рис 5.9), содержащая описания альтернатив. Альтернативы подлежат предварительной оценке по критериям качества. Возможны два способа проведения экспертной оценки. По первому способу оценка альтернатив всех функциональных подсистем осуществляется по единому множеству критериев (частный случай). По второму способу оценка каждой функциональной подсистемы мероприятий и соответствующих ей альтернатив проводится по различным уникальным подмножествам критериев (наиболее общий случай).

В первом и втором способах оценки имеется возможность использовать три вида структур критериев качества, по которым предполагается ранжировать альтернативы и отыскивать рациональные элементы в каждой строке морфологической таблицы. Используемая по усмотрению исследователя структура критериев может представлять один критерий, вектор критериев, иерархическую структуру критериев. Приведенные три вида структур критериев реализуемы методом анализа иерархий.

Далее экспертным путем определяется относительная степень предпочтительности критериев качества между собой для установления их весомости (значимости) при решении конкретной задачи. Следующим этапом является оценка альтернатив относительно критериев самого нижнего иерархического уровня. Степень предпочтительности устанавливается экспертом методом попарного сравнения или методом сравнения относительно стандартов.

По полученным экспертным данным вычисляются векторы приоритетов альтернатив ( ) по всем критериям качества, вплоть до критерия, определяющего фокус (вершину) иерархии. Аналогично рассчитываются векторы, устанавливающие приоритет альтернатив, находящихся во всех остальных строках морфологической таблицы. Для последующего синтеза рациональных целостных вариантов систем в морфологическую таблицу заносятся векторы приоритетов альтернатив по интересующим исследователя критериям качества.

Это могут быть фокусы иерархий критериев или критерии, находящиеся на промежуточных уровнях иерархий. В рассматриваемом примере морфологическая таблица содержит для определенности векторы приоритетов альтернатив относительно всех критериев и фокусов иерархий. Лучшей альтернативой в каждой строке морфологической таблицы по тому или иному критерию является та, которая имеет наибольшее значение в соответствующем векторе приоритетов.

При поиске рациональных вариантов в морфологическом множестве могут решаться две отличающиеся друг от друга задачи.

Решение первой задачи сводится к отысканию в морфологическом множестве одного или нескольких целостных вариантов систем, удовлетворяющих аддитивной или мультипликативной целевой функции. При этом на морфологической таблице генерируются все варианты технических систем алгоритмом полного перебора. Аддитивная и мультипликативная целевые функции в этой задаче определяются следующим образом.

Аддитивная целевая функция. Найти подмножество S Î W, для элементов которого

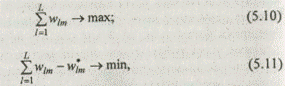
где S — подмножество искомых целостных вариантов систем;

W — морфологические множества всех систем, содержащихся в исследуемой морфологической таблице, имеющие размерность N , определяемую по выражению:

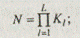
L — число функций системы (число строк морфологической таблицы);

w_lm, w * _lm, — соответственно рассматриваемое и наилучшее интегральные по нескольким критериям качества значения векторов приоритетов, соответствующих альтернативам A_lm, и А*_lm, входящих в i-й вариант синтезируемой системы и наилучшей по рассматриваемым критериям альтернативы;

N — размерность морфологического множества;

K_l — число способов (альтернатив А _lm для реализации i-й функции системы.

Аддитивные модели базируются на предположении о том, что качество системы (экономической, управленческой и т. д.), т. е. ее ценность, полезность, эффективность, определяется суммой эффектов от каждого ее свойства. Частной и широко применяемой на практике формой выражения аддитивного показателя качества является взвешенная арифметическая (5.10), (5.11). Наряду с аддитивной моделью, базирующейся на применении средневзвешенной арифметической, используются и другие виды показателей качества, основанные на других принципах, например на принципе мультипликативности, т. е. не сложения, а перемножения эффектов. В этом случае показатель качества выражается средневзвешенной, но не арифметической, а геометрической.

Мультипликативная целевая функция. Найти подмножество S Î W, для элементов которого

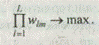
Вопрос о том, какая из этих двух средневзвешенных более адекватно отражает поведение человека, принимающего решение с учетом не одного, а нескольких показателей, был предметом научной дискуссии Галилея с Ноццолино еще в 17в. (Галилей отдавал предпочтение среднегеометрическому, а Ноццолино — среднеарифметическому). С тех пор многие ученые — специалисты в области статистики, психофизиологии и другие высказывали различные теоретические доводы в пользу каждой из этих двух средневзвешенных. В различных областях науки и практики аддитивный показатель качества в виде средневзвешенной арифметической используется гораздо чаще, чем другие виды средневзвешенных (например, среднегеометрическая). Однако использование аддитивного показателя качества требует, чтобы между относительными показателями любых свойств существовала независимость по предпочтению.

Решение второй задачи сводится к поиску в морфологическом множестве подмножества вариантов систем, наиболее сходных с поисковым заданием. Целевая функция в этой задаче определяется следующим образом: найти подмножество S Î W, для элементов которого

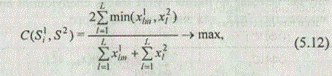
где С(S_i ¹, S ²) — мера сходства между описанием рассматриваемого варианта системы S_i ¹ и описанием поискового задания S ² ;

x ¹ _lm , x ² _l — числовые значения критериев качества, характеризующие соответственно рассматриваемый вариант системы и поисковое задание;

L — может иметь два значения и определять либо число обобщенных функциональных подсистем, либо число критериев качества, которыми на количественном уровне охарактеризованы описания S_i ¹ и S²;

т — порядковый номер альтернативы в строке морфологической матрицы.

Первое значение индекс L имеет в том случае, если x ¹ _lm и x ² _l представляют интегральную оценку по множеству критериев качества, характеризующих альтернативу А _lm, являющуюся компонентом описания рассматриваемой системы S_i ¹ и описания системы S ² , выступающей в роли поискового задания (это могут быть прототип, идеальная система, желаемая система).

Второе значение индекс L имеет в случае, когда x ¹ _lm и x ² _l представляют неинтегральные по множеству критериев качества значения, характеризующие в целом альтернативу рассматриваемых вариантов систем и поискового задания. Верхние индексы указывают на принадлежность к рассматриваемому варианту системы (индекс равен единице) и поисковому заданию (индекс равен двум).

Если в выражении (5.12) х¹ _{l т} и x ² _i отражают интегральные значения всего множества критериев, характеризующих альтернативы, то при необходимости учета различной степени влияния на меру сходства функциональных подсистем в числитель и знаменатель после знака суммы необходимо добавить весовой коэффициент w_l и присвоить соответствующие значения каждой функциональной подсистеме. Если x ¹ _lm и х² _l , отражают значения индивидуальных критериев качества, то для учета влияния на меру сходства (5.12) одновременно функциональных подсистем и критериев качества необходимо ввести два весовых коэффициента. В этом случае целевая функция будет иметь следующий вид: найти подмножество S Î W, для элементов которого

где r_l — весовой коэффициент, определяющий вклад в меру сходства критериев качества обобщенной функциональной подсистемы ОФПС_l;

w_lp — весовой коэффициент, определяющий вклад в меру сходства критерия качества К _p по которому оценивается ОФПС_l;

L — число обобщенных функциональных подсистем;

P — число критериев качества, характеризующих альтернативы А _lm и А _l , причем Р = 1,2,..., r при l = 1; Р = 1,2,..., s при l = 2; Р = 1,2,..., t при l = h;

x ¹ _lpm - оценка по критерию качества К_р альтернативы А _lm, участвующей в синтезе и принадлежащей обобщенной функциональной подсистеме ОФПС_l ;

x ² _lp — оценка по критерию качества К_р обобщенной функциональной подсистемы ОФПС_l, принадлежащей системе, представляющей поисковое задание.

Рассмотрим примеры синтеза вариантов систем на основе аддитивной целевой функции и на принципе определения меры сходства между вариантом и поисковым заданием. Используем для этой цели ранее построенную морфологическую таблицу (см. рис. 5.9).

Строго упорядочим по значимости обобщенные функциональные подсистемы (строки) сверху вниз и альтернативы в каждой строке — слева направо. Осуществим синтез всех вариантов систем по лексикографическому принципу, подобному упорядочению слов в словарях. Для каждого варианта рассчитаем значение аддитивной целевой функции по выражению (5.10). Упорядочив варианты в направлении уменьшения значений целевой функции (табл. 5.13), можно определить подмножество наиболее эффективных решений, которые подлежат дополнительному анализу. К таким решениям относятся, например, варианты 16, 10 и 4.

Таблица 5.13