Для повышения степени объективности и качества процедуры принятия решений целесообразно учитывать мнения нескольких экспертов. С этой целью проводится групповая экспертиза, причем множество экспертов может быть подразделено на несколько подмножеств в зависимости от области экспертизы [З], определяемой характером критериев, используемых в иерархии. Оценка весомости критериев и альтернатив с учетом данного подхода предполагает привлечение специалистов-управленцев, маркетологов, производственников, специалистов-теоретиков и т. п. (рис. 2.4).
Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующему соотношению:
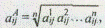 (2.6)
(2.6)
где a А ij — агрегированная оценка элемента, принадлежащего i-й строке и j-му столбцу матрицы парных сравнений;
п — число матриц парных сравнений, каждая из которых составлена одним экспертом.
Логичность критерия (2.6) становится очевидной, если два равноценных эксперта указывают при сравнении объектов соответственно оценки а и 1/а, что при вычислении агрегированной оценки дает единицу и свидетельствует об эквивалентности сравниваемых объектов.
Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены на уровне элементов матриц, если однородность составленных матриц достаточна и удовлетворяет условию OO ≤ 0,10. Покажем это на следующем примере.
Пусть заданы суждения двух экспертов в виде матриц попарных сравнений [A1] и [A2]:
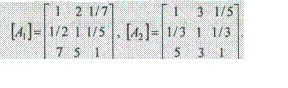
Для этих матриц собственные векторы W А i , максимальные собственные значения λmax и оценки однородности (ИО; OO) имеют следующий вид:
для матрицы [A1]
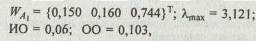
Для матрицы [A2],
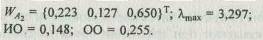
Осреднение на уровне элементов собственных векторов дает
WA= {0,184 0,117 0,699}T.
Осредняя элементы матриц [A1] [A2], получим матрицу [А3]:
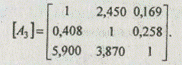
Правый собственный вектор матрицы [А3] следующий:
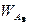 = {0,184 0,116 0,699}T.
= {0,184 0,116 0,699}T.
Сравнивая два собственных вектора Wa и 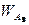 определенных двумя разными способами, можно убедиться в их совпадении, даже несмотря на то, что однородность суждений эксперта, заполнившего матрицу [A2], была неудовлетворительной (OO = 0,255 > 0,10).
определенных двумя разными способами, можно убедиться в их совпадении, даже несмотря на то, что однородность суждений эксперта, заполнившего матрицу [A2], была неудовлетворительной (OO = 0,255 > 0,10).
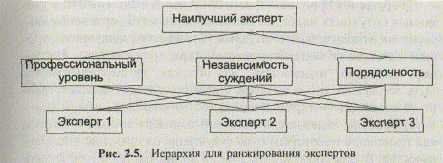
В достаточно ответственных задачах при оправданных затратах на экспертизу осреднение суждений экспертов проводится с учетом их квалификации ("веса"). Для определения весовых коэффициентов экспертов целесообразно использовать иерархическую структуру критериев (рис. 2.5).
Расчет агрегированной оценки в случае привлечения п экспертов, имеющих различную значимость, осуществляется по формуле
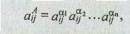
где aakij — оценка объекта, проведенная k-м экспертом с весовым коэффициентом ak ; при этом а1 + а2 +...+ а n= 1.
Дата: 2018-11-18, просмотров: 421.