В практических задачах количественная (кардинальная) и транзитивная (порядковая) однородность (согласованность) нарушается, поскольку человеческие ощущения нельзя выразить точной формулой. Для улучшения однородности в числовых суждениях, какая бы величина aij ни была взята для сравнения i-го элемента с j-м, aij приписывается значение обратной величины, т. е. аij = 1/aij. Отсюда следует, что если один элемент в а раз предпочтительнее другого, то последний только в 1/а раз предпочтительнее первого.
При нарушении однородности ранг матрицы отличен от единицы и она будет иметь несколько собственных значений. Однако при небольших отклонениях суждений от однородности одно из собственных значений будет существенно больше остальных и приблизительно равно порядку матрицы. Таким образом, для оценки однородности суждений эксперта необходимо использовать отклонение величины максимального собственного значения λmax от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или отношением однородности (OO) в соответствии со следующими выражениями:
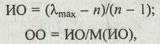
где М(ИО) — среднее значение (математическое ожидание) индекса однородности случайным образом составленной матрицы парных сравнений [E], которое основано на экспериментальных данных (табл. 2.3), полученных в работе [2].
Таблица 2.3
Среднее значение индекса однородности в зависимости от порядка матрицы
| Порядок матрицы (п) | М(ИО) | Порядок матрицы (и) | М(ИО) | Порядок матрицы (п) | М(ИО) |
|
| 1 | 0,00 | 6 | 1,24 | 11 | 1,51 | |
| 2 | 0,00 | 7 | 1,32 | 12 | 1,48 | |
| 3 | 0,58 | 8 | 1,41 | 13 | 1,56 | |
| 4 | 0,90 | 9 | 1,45 | 14 | 1,57 | |
| 5 | 1,12 | 10 | 1.49 | 15 | 1,59 |
В качестве допустимого используется значение OO ≤ 0,10. Если для матрицы парных сравнений отношение однородности OO > 0,10, то это свидетельствует о существенном нарушении логичности суждений, допущенном экспертом при заполнении матрицы, поэтому эксперту предлагается пересмотреть данные, использованные для построения матрицы, чтобы улучшить однородность.
Синтез приоритетов на иерархии и оценка ее однородности
Иерархический синтез
Иерархический синтез используется для взвешивания собственных векторов матриц парных сравнений альтернатив весами критериев (элементов), имеющихся в иерархии, а также для вычисления суммы по всем соответствующим взвешенным компонентам собственных векторов нижележащего уровня иерархии. Ниже рассматривается алгоритм иерархического синтеза с учетом обозначений, принятых в предыдущей иерархии (см. рис. 2.1).
Ш а г 1. Определяются векторы приоритетов альтернатив 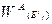 относительно элементов Eij предпоследнего уровня иерархии (i = S). Здесь через Eij обозначены элементы иерархии, причем верхний индекс i указывает уровень иерархии, а нижний индекс j — порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив WAS относительно уровня иерархии S осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.2) и (2.3) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:
относительно элементов Eij предпоследнего уровня иерархии (i = S). Здесь через Eij обозначены элементы иерархии, причем верхний индекс i указывает уровень иерархии, а нижний индекс j — порядковый номер элемента на уровне. Вычисление множества векторов приоритетов альтернатив WAS относительно уровня иерархии S осуществляется по итерационному алгоритму, реализованному на основе соотношений (2.2) и (2.3) по исходным данным, зафиксированным в матрицах попарных сравнений. В результате определяется множество векторов:
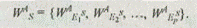
Ш а г 2. Аналогичным образом обрабатываются матрицы попарных сравнений собственно элементов E i j . Данные матрицы построены таким образом, чтобы определить предпочтительность элементов определенного иерархического уровня относительно элементов вышележащего уровня, с которыми они непосредственно связаны. Например, для вычисления векторов приоритетов элементов третьего иерархического уровня (см. рис. 2.1) обрабатываются следующие три матрицы попарных сравнений:
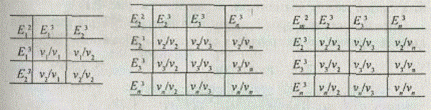
В матрицах через vj обозначен вес, или интенсивность, Е j -го элемента.
В результате обработки матриц попарных сравнений определяется множество векторов приоритетов элементов:
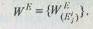
Полученные значения векторов 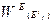 используются впоследствии при определении векторов приоритетов альтернатив относительно всех элементов иерархии.
используются впоследствии при определении векторов приоритетов альтернатив относительно всех элементов иерархии.
Шаг 3. Осуществляется собственно иерархический синтез, заключающийся в последовательном определении векторов приоритетов альтернатив относительно элементов Е i j находящихся на всех иерархических уровнях, кроме предпоследнего, содержащего элементы Е S j. Вычисление векторов приоритетов проводится в направлении от нижних уровней к верхним с учетом конкретных связей между элементами, принадлежащими различным уровням. Вычисление проводится путем перемножения соответствующих векторов и матриц.
Общий вид выражения для вычисления векторов приоритетов альтернатив определяется следующим образом:
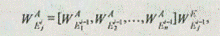
где 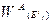 — вектор приоритетов альтернатив относительно элемента E1i -1, определяющий j-й столбец матрицы;
— вектор приоритетов альтернатив относительно элемента E1i -1, определяющий j-й столбец матрицы;
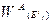 — вектор приоритетов элементов E1i -1, E2i -1,..., Eni -1, связанных с элементом Ej вышележащего уровня иерархии.
— вектор приоритетов элементов E1i -1, E2i -1,..., Eni -1, связанных с элементом Ej вышележащего уровня иерархии.
Ниже приведен конкретный пример по вычислению векторов приоритетов альтернатив относительно элементов третьего (E3j), второго (Е2j ) и первого (Е1 j ) уровней иерархии с учетом конкретных связей между элементами иерархии (см. рис. 2.1).
Определение векторов приоритетов альтернатив для элементов второго уровня осуществляется следующим образом:
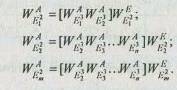
Результирующий вектор приоритетов альтернатив относительно корневой вершины иерархии Е11 вычисляется следующим образом:
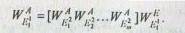
Рассмотренная модификация МАИ может эффективно применяться при решении широкого класса социально-экономических и управленческих задач.
Дата: 2018-11-18, просмотров: 706.