Реальные системы автоматического регулирования в большинстве сво­ем нелинейны, однако поддаются линеаризации. К системам, которые не могут быть линеаризованы, относятся системы, содержащие релейные и подобные им элементы, с характеристиками, показанными на рис. 70.

а)           б)              в)               г)             д)                 е)

Рис. 70.

Характеристика на рис. 70, а называется релейной идеальной. Такую характеристику имеет реле с малым ходом якоря, когда отличием тока срабатывания от тока отпускания можно пренебречь. На рис. 70, б – идеальная с зоной нечувствительности. Характеристика соответствует идеализированному поляризован­ному реле. На рис. 70, в – характеристика релейная с гистерезисом – соответствует большинству релейных устройств. Характеристика на рис. 70, г является реальной характеристикой поляризованного реле, характеристики на рис. 70, д, е – с насыщением и «люфт» – характерны для устройств с ограничением параметров в механических конструкциях.

В отличие от линейных систем в нелинейных наличие автоколебаний может соответствовать устойчивому режиму, если амплитуда колебаний меньше допустимой ошибки. Частота колебаний в этом случае также представляет интерес, так как определяет износ элементов системы. Пример системы с релейным элементом показан на рис. 71.

Рис. 71.

Температура в камере 1 поддерживается подачей горячего воздуха через сопло 2. Расход воздуха регулируется заслонкой 3. Изменение положения заслонки производится через винтовой механизм 4 и редуктор 5 двигателем постоянного тока последовательного возбуждения М. Температура внутри камеры измеряется терморезистором R, включенным в плечо мостовой схемы. В диагональ моста включено поляризованное реле К1. При отклонении температуры от заданной срабатывает реле K1, подключая двигатель М в ту или другую сторону, который перемещает заслонку, изменяя ее положение в сторону, соответствующую уменьшению рассогласования. Релейное звено в данном случае – поляризованное реле K1, имеющее статическую характеристику, показанную на рис. 70, г.

Для анализа релейной системы или любой системы с нелинейным элементом линейные звенья объединяют общей передаточной функцией, чтобы структурная схема приняла вид удобный для анализа (рис. 72), разделив линейную и нелинейные части. Для этого используются правила переноса звеньев структурной схемы, включая и объ­ект регулирования.

Рис. 72.

Если чувствительность реле высока, то можно считать, что характеристика имеет форму рис. 70, б (идеализация в учебных целях). Тогда очевидно, что статическую характеристику можно разбить на три зо­ны, где у<0; у=0; и у>0. В каждой из этих зон система ли­нейна и описывается своим уравнением. Переключение реле происходит не во времени, а при определенных значениях тока в обмотке (входной величи­ны на статической характеристике), т. е. определяется свойствами системы и характерном возмущения.

Таким образом, переходный процесс в релейной системе может быть найден путем решения различных линейных уравнений по участкам, границы между которыми заданы значениями Х. При этом, решая уравнения каждого участ­ка, в качестве начальных условий для него берут значения переменных, полу­ченных в конце предыдущего. Такой метод называется методом припасовывания. Для реальной характеристики реле рис. 70, г участков будет больше.

Для улучшения процесса регулирования в релейных системах при­меняют те же самые средства, что и в непрерывных линейных системах. К этим средствам относятся:

– последовательные корректирующие устройства (введение дифференци­рующих и интегрирующих звеньев);

– параллельные корректирующие устройства (введение обратных связей, охватывающих отдельные звенья или участки структурной схемы);

– корректирующие устройства, работающие по возмущению (принцип комбинированного управления).

Кроме всего вышесказанного, имеет значение:

– ширина зоны нечувствительности – для большинства случаев при медленном изменении регулируемой величины способствует затуханию колебаний;

– ширина гистерезисной петли, которая чаще всего способствует раскачиванию системы.

Метод припасовывания недостаточно нагляден. Для систем, динамика которых описывается уравнениями 2-го порядка, более наглядным является метод фазовой плоскости. Вообще, если система описывается уравнением n-го порядка, то ее состояние соответствует точке в n-мерном пространстве. Движение системы во времени при постоянстве внешнего воздействия будет изображаться семейством траекторий, каждая из которых соответствует определенному начальному состоянию. В переходном процессе система характеризуется отклонением регулируемой величины ∆у и скоростью его изменения 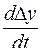. Для систем с уравнением 2-го порядка фазовое пространство – плоскость. Совокупность траекторий системы называют фазовым портретом. Метод фазовых траекторий применим и к линейным и к нелинейным системам. Сначала рассмотрим фазовые траектории линейных систем. Допустим, переходный процесс представляет собой периодические колебания с постоянной частотой и амплитудой и начи­нается в точке ∆у₀ при t = 0. Фазовую плоскость строим в координатах  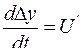и ∆у =U. Движение точки по траектории (рис. 73) по участкам ABCDEF, соответствующее периоду колебаний, на фазовой плоскости, будет представлять собой замкнутый контур, рис. 74. При синусоидальных колебаниях это эллипс (рис. 74).

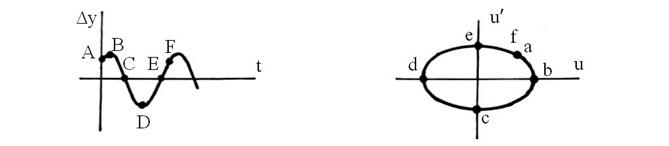
Рис. 73.                                  Рис. 74.

При затухающих колебаниях (рис. 75, а) фазовым портретом будет сходящаяся спираль (рис. 75, б).

а)                                                     б)

Рис. 75.

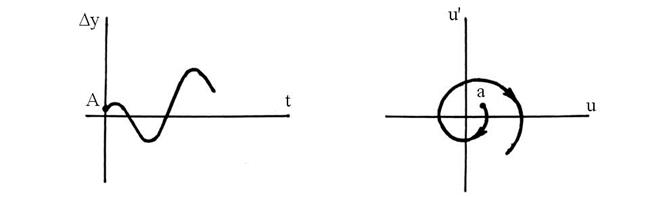
Если переходный процесс затухает при ∆у ≠ 0 (статическая ошибка), то скручивание спирали будет вокруг этой точки, рис. 76.

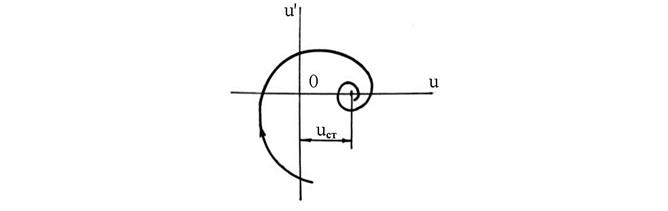
Рис. 76

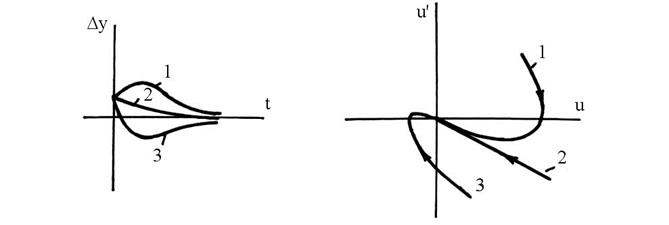
Исходя из вышесказанного расходящийся процесс на фазовой плоскости будет изображаться расходящейся спиралью, рис. 77, а, б. Затухающие апериодические процессы различных видов сходятся к началу координат фазовой плоскости (рис. 78, а) незатухающие – расходятся, рис. 79, а, б.

а)                                                б)

Рис. 77.

а)                                                б)

Рис. 78.

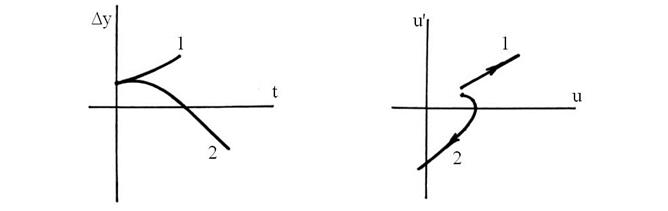
а)                                                б)

Рис. 79.

Для построения фазового портрета релейной системы необходимо составить уравнения по участием релейной характеристики и исключить из них пе­ременную t методом подстановки, учитывая обозначения по осям фазового портрета. Полученное дифференциальное уравнение затем интегрируют и изменяют в полученном выражении постоянную интегрирования С от 0 до ∞. Таким образом, получается фазовый портрет релейной системы. При идеальной релейной характеристике (рис. 70, а) нелинейного звена фазовый портрет системы показан на рис. 80, а, для системы с звеном с характеристикой рис. 70, б – на рис. 80, б, а системы с поляризованным реле при характеристике рис. 70, г – на рис. 80, в.

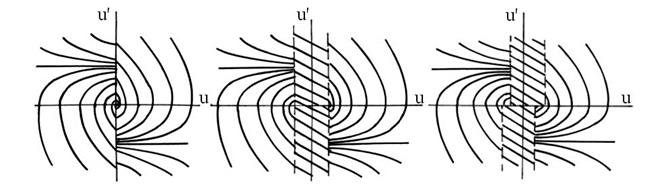
а)                           б)                             в)

Рис. 80.

Если фазовый портрет дает расходящуюся картину, то производится коррекция, как уже было показано ранее.

Для анализа систем с дифференциальными уравнениями выше 2-го порядка применяют более сложные методы гармонической линеаризации, абсолютной устойчивости и другие. Для получения достоверного результата по устойчивости нелинейных систем высоких порядков пользуются различными методами, совпадение выводов которых позволяет получить правильный ответ.