Устойчивость САР
Переходный процесс в автоматической системе зависит как от свойств системы, так и от вида возмущения. В переходном процессе две составляющие: свободное движение, определяемое начальными условиями и свойствами системы; вынужденное движение, которое определяется возмущением и также свойствами системы. Свободное движение должно с течением времени стремиться к нулю, так как это определяет устойчивость системы. В устойчивых САР переходный процесс затухает  (рис. 62), а в неустойчивых – расходится (рис. 63).
(рис. 62), а в неустойчивых – расходится (рис. 63).
Для аналитического определения характера переходного процесса необходимо составить дифференциальное уравнение движения системы в переходном процессе и проинтегрировать его, т. е. определить y(t).
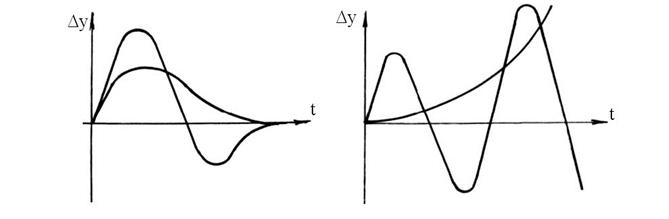
Рис. 62. Рис. 63.
В общем виде дифференциальное уравнение движения относительно Δу при затухающем процессе можно записать как
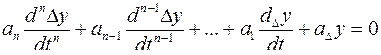 .
.
Нуль в правой части означает, что процесс затухает. Коэффициенты  являются постоянными, определяемыми параметрами системы. Характеристическое уравнение этого дифференциального уравнения имеет вид
являются постоянными, определяемыми параметрами системы. Характеристическое уравнение этого дифференциального уравнения имеет вид
 , (4)
, (4)
где р – оператор.
Известно, что корни такого уравнения в общем случае есть комплексные числа вида  . Необходимым и достаточным условием устойчивости является отрицательное значение всех вещественных частей корней характеристического уравнения. Если хотя бы один
. Необходимым и достаточным условием устойчивости является отрицательное значение всех вещественных частей корней характеристического уравнения. Если хотя бы один 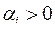 , то система неустойчива. Если же все
, то система неустойчива. Если же все  , но имеются нулевые или чисто мнимые корни, то система имеет переходный процесс с незатухающими колебаниями, так называемая консервативная система, которая также считается неустойчивой.
, но имеются нулевые или чисто мнимые корни, то система имеет переходный процесс с незатухающими колебаниями, так называемая консервативная система, которая также считается неустойчивой.
Чем выше порядок дифференциального уравнения системы, тем сложнее искать корни характеристического уравнения. Поэтому были разработаны различные критерии устойчивости, применяемые в инженерных расчетах и позволяющие не решать уравнений. Рассмотрим некоторые из них, наиболее часто применяемые.
1. Критерий Раусса - Гурвица.
Этот критерий позволяет определить устойчивость по коэффициентам уравнения системы. Для этого из коэффициентов характеристического уравнения составляется квадратная матрица, называемая определителем Гурвица. В первой строке матрицы записываются все нечетные коэффициенты, во второй – все четные. При отсутствии какого-либо коэффициента, а также вместо коэффициентов с индексами больше n и меньше нуля, пишется 0. Например, для характеристического уравнения 4-го порядка:

| a3 | a1 | 0 | 0 |
| ay | a2 | a0 | 0 |
| 0 | a3 | a1 | 0 |
| 0 | ay | a2 | a0 |
и в общем виде 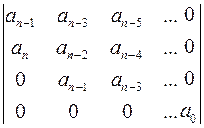
Система автоматического регулирования устройства, если определитель Гурвица, его диагональные миноры и все коэффициенты 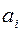 положительны. Таким образом, кроме положительности коэффициентов, необходимо определить знак диагональных миноров, отмеченных выше линиями на матрице для уравнения 4-го порядка. Достоинство критерия – простота. Однако применить критерий можно только при постоянстве параметров, и он не позволяет оценить запас устойчивости и быстроту затухания переходного процесса. Обычно применяют критерий для уравнений не выше 4-го порядка.
положительны. Таким образом, кроме положительности коэффициентов, необходимо определить знак диагональных миноров, отмеченных выше линиями на матрице для уравнения 4-го порядка. Достоинство критерия – простота. Однако применить критерий можно только при постоянстве параметров, и он не позволяет оценить запас устойчивости и быстроту затухания переходного процесса. Обычно применяют критерий для уравнений не выше 4-го порядка.
2. Критерий Найквиста.
По этому критерию об устойчивости замкнутой системы судят по АФЧХ разомкнутой. Для этого необходимо структурную схему замкнутой системы свести к виду, показанному на рис. 64. Затем разомкнуть систему и определить передаточную функцию W(p) = W1(p)W2(p). По W(p) строят АФХЧ (годограф). Система устойчива, если годограф разомкнутой системы не охватывает точку с координатами 0;–1, рис. 65.
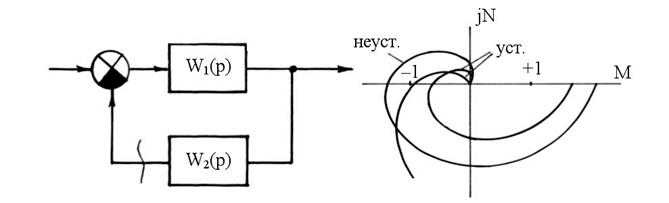
Рис. 64. Рис. 65.
В этом критерии можно определить запас устойчивости по модулю и по фазе. Для этого необходимо провести окружность радиусом R=1, рис. 66.
Проведя радиус через точку пересечения А, можно определить запас устойчивости по фазе как угол 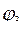 и запас по модулю как отношение отрезков СВ/СО, или
и запас по модулю как отношение отрезков СВ/СО, или 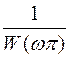 , где
, где 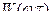 – значение АФЧХ разомкнутой системы при частоте
– значение АФЧХ разомкнутой системы при частоте 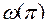 , соответствующей
, соответствующей 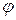 = 180° (точка В), рис. 66.
= 180° (точка В), рис. 66.

Рис. 66.
3. Критерий устойчивости по ЛАЧХ.
Этот критерий представляет собой интерпретацию критерия Найквиста при помощи  и
и  разомкнутой САР. Замкнутая система устойчива, если
разомкнутой САР. Замкнутая система устойчива, если 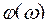 разомкнутой системы при частоте среза
разомкнутой системы при частоте среза 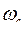 не достигает 180°. При большем сдвиге фаза выходного сигнала меняется на противоположную и система, вместо того, чтобы идти к положению равновесия, уходит от него, рис. 67. Запас по фазе определяется углом
не достигает 180°. При большем сдвиге фаза выходного сигнала меняется на противоположную и система, вместо того, чтобы идти к положению равновесия, уходит от него, рис. 67. Запас по фазе определяется углом 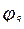 при частоте среза
при частоте среза 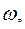 (рис. 67), а по модулю
(рис. 67), а по модулю 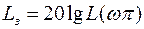 , где
, где 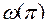 – частота, при которой
– частота, при которой 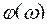 достигает 180°.
достигает 180°.
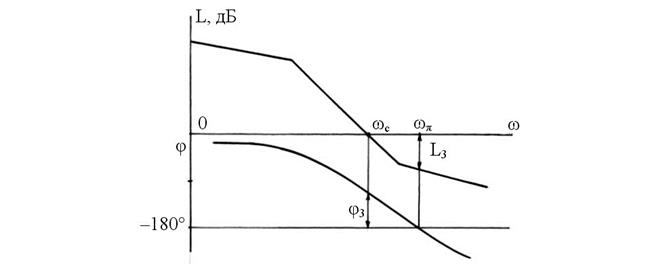
Рис. 67.
Для обеспечения удовлетворительных показателей переходного процесса устанавливают LЗ ≤ 10 – 20 дБ и 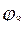 = 36–60°.
= 36–60°.
Различают структурно-устойчивые и структурно-неустойчивые системы. Для первых устойчивость зависит от значения ее параметров. Если при любых параметрах САР неустойчива, она называется структурно-неустойчивой. Способ определения устойчивости по логарифмическим характеристикам хорошо разработан и является инженерным. Здесь легко определить желательную характеристику 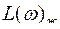 , выяснить, какие звенья оказывают наибольшее влияние на устойчивость и какую характеристику должны они иметь.
, выяснить, какие звенья оказывают наибольшее влияние на устойчивость и какую характеристику должны они иметь.
Качество регулирования
Если система устойчива, то следующим этапом является выяснение качества регулирования. Наглядное представление о качестве регулирования системы дает переходная характеристика. У устойчивой системы при мгновенном скачкообразном воздействии переходный процесс может быть апериодическим, или колебательным, рис. 68, а, б.
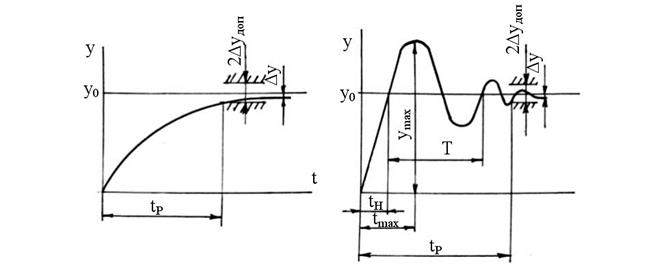
Рис. 68.
Общими показателями качества для обоих переходных процессов является статическая ошибка Δу и время регулирования tp. Статическая ошибка – это ошибка, которая определяется как limΔy(t) при t → ∞. Ошибка должна быть меньше допустимой Δyдоп. Время регулирования tp определяется как время, за которое y(t) достигнет значения у0 с требуемой точностью, т. е. кривая переходного процесса перестанет выходить за пределы заштрихованной области, ширина которой равна 2Δудоп, рис. 68. Допустимую ошибку в технике обычно устанавливают 5 или 10 %, но может быть и точнее, например 2 %.
Для колебательного процесса показателями качества дополнительно являются также перерегулирование σ и колебательность М.
Перерегулирование определяется как
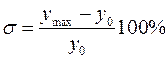 .
.
Перерегулирование обычно допускается не более 20–30 %.
Колебательность системы определяется числом переходов через положение равновесия у0 . В большинстве случаев допускается М = 2…3. Кроме перечисленных показателей быстродействие САР может характеризоваться также временем первого согласования tн , временем достижения первого максимума tmax и периодом Т, рис. 68, б.
Существует и интегральная оценка качества, которая заключается в следующем. Если перестроить графики переходных процессов (рис. 68), чтобы у0 был на линии абсцисс, то получим кривые, показанные на рис. 69 а, б.
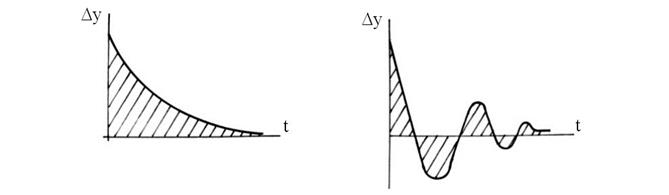
Рис. 69.
Величина заштрихованной в обоих случаях площади определяется скоростью затухания переходного процесса, т.е. качеством регулирования системы. Для апериодического процесса площадь под кривой (рис. 68, а):
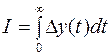 ,
,
где Δу – отклонение регулируемой величины от заданного значения у0, о качестве судят по квадратичной зависимости:
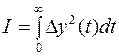 .
.
Интегральный показатель качества может быть вычислен без построения кривой переходного процесса по уравнению h(t). Недостатком интегральных оценок является отсутствие наглядного соответствия между значениями показателей I и другими характеристиками переходных процессов.
Определение формы кривой переходного процесса аналитически (прямой метод) затруднительно, особенно при уравнении высоких порядков и не достаточно информативно, когда требуется выяснить влияние отдельных параметров на показатели качества. Для этих целей разработаны косвенные методы. Однако и эти методы вряд ли можно причислить к исключительно простым. На сегодняшний день при анализе широко используются вычислительная техника и пакеты программ, позволяющие реализовать вышеописанные методы определения устойчивости и качества регулирования быстро и с высокой точностью.
Коррекция САР
Если спроектированная САР не удовлетворяет требованиям запаса устойчивости и качества регулирования, то возникает необходимость в ее коррекции. Без изменения структурной схемы системы можно только повысить общий коэффициент усиления и таким образом снизить статическую ошибку. Но в этом случае повышается скорость регулирования, переходный процесс становится колебательным, или колебания усиливаются, и возможны потеря устойчивости или ухудшение временных показателей качества. Для коррекции в структурную схему вводят дополнительные корректирующие звенья, подключаемые последовательно и параллельно. Положительная обратная связь увеличивает коэффициент усиления звена, отрицательная уменьшает постоянную времени, улучшает устойчивость и изменяет тип звена. При коррекции устойчивости сначала строят ЛАЧХ исходной системы и определяют ЛАЧХ желаемую, изменяя значение 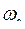 . Затем по разности ординат этих характеристик
. Затем по разности ординат этих характеристик 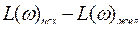 находят
находят 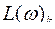 – ЛАЧХ корректирующего звена. Отсюда определяют W(p)k и выбирают звено как реальное устройство, обычно как элемент электрической схемы в виде сочетания параметров
– ЛАЧХ корректирующего звена. Отсюда определяют W(p)k и выбирают звено как реальное устройство, обычно как элемент электрической схемы в виде сочетания параметров
RC-цепочки. После этого, учитывая реальные параметры подобранного корректирующего звена, определяют ЛАЧХ скорректированной системы и определяют ее h(t). По характеру кривой h(t) определяют качество регулирования? и если параметры удовлетворяют предъявляемым требованиям, то коррекцию прекращают, а если нет, то производят заново. Для коррекции имеются разработанные рекомендации и номограммы для определения показателей качества регулирования. В настоящее время для расчета САР широко применяется вычислительная техника с пакетами программ, облегчающими и ускоряющими процесс проектирования.
Дата: 2018-11-18, просмотров: 420.