Відношенням на множині називається будь-яке правило, яке деяким елементам цієї множини становить у відповідність якісь інші елементи цієї множини.
Відношення між двома об’єктами називається бінарним.
Для кожного відношення маємо множину впорядкованих пар. Впорядковані пари зустрічаються в Декартовому добутку АхА<<
*Відношення між елементами множини Х або відношенням, визначеним у множині Х, називають будь-яку підмножину Декартового добутку ХхХ, або декартового квадрата 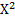
Відношення позначають великими прописними латинськими літерами P,Q,R,S .Записують: ХRY
Відношення можна позначати графічно для цього існує поняття «граф2.
Способи задання відношень:
1. Відношення у множині можна задати шляхом перелічування всіх пар елементів множини, що знаходяться у цьому відношенні.
*Те ж відношення можна задати за допомогою графа.
2. Відношення у множині можна задати, вказати характеристичну властивість всіх пар елементів.
11.Властивості відношень.
1. властивість рефлективності.
Відношення R у множині х називається рефлексивним, якщо кожен елемент множини Х знаходиться у відношенні R сам до себе.
Короткий запис: Х <=> Х RХ
2.Властивість антирефлексивності
відношення R на множині Х називається антисиметричним, якщо кожен елемент Х не є у відношенні R сам до себе
корот. Запис 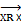 (не є)
(не є)
3. властивість симетричності
Відношення R на множині Х називається симетричним, якщо з того, що елемент Х знаходиться у відношенні R до елемента У , випливає, що елемент У знаходиться у відношенні R до елемента Х.
Короткий запис: Х R У<=> У RХ
4. Властивість анти симетричності:
Короткий запис: Х RУ і Х≠У не <=>У RХ
5. Властивість транзитивності (3 елементи)
Відношення R у множині Х називається транзитивним, якщо воно з того, що елемент Х знаходиться у відношенні R до елемента У, а елемент У знаходиться у відношенні R до елемента Z, то елемент Х також перебуває у відношенні R до елемента Z.
Короткий запис: Х RУ і У R Z, то Х R Z
Відношення еквівалентності
Відношення у множині називається відношенням еквівалентності, якшо воно рефлексивне, симетричне і транзитивне.
А=
R «Бути рівними
В даному відношенні присутні відношення рефлексивності (і на графі петля, пари з рівними компонентами елементами). Присутнє відношення симетричності два елементи з’єднані стрілками (з 2, 2з ) ав парах компоненти міняються місцями. Присутнє відношення транзитивності. Отже робимо висновок: дане відношення є відношенням еквівалентності
Якщо у множині Х задано еквівалентності, то воно розбиває дану множину на підмножини, попарно не перетинаються → називається класи еквівалентності.
Відношення порядку
Відношення R на множині Х, називається відношенням порядку, якщо воно транзитивне і антисиметричне.
Множина із заданим на ній відношенням порядку називається впорядкованою множиною.
Залежно від видів відношень порядку розрізняють і види впорядкованих множин.
14.Поняття Відповідності. Відповідність, обернена даній.
Означення. Відповідністю між елементами двох множин (бінарною відповідністю) називається підмножина декартового добутку ХЧУ.
Множина Х називається множиною відправлення, а множина Y – множиною прибуття відповідності. Разом їх називають базовими множинами відповідності.
15.Взаємнооднозначні відповідності. Рівно потужні множини.
Взаємно однозначними відповідностями називаються відповідності, якщо кожному елементу множини Х відповідає єдиний елемент множини У, і кожний елемент множини У відповідає єдиному елементу множини Х.
У початковій школі поняття взаємно однозначної відповідності використовується неявно: на даному понятті будується лічба предметів, їх порівняння.
Акщо відповідності взаємно однозначні, то кількість елементів відповідних множин рівні.
Приклад: Множина А=  множина букв у слові «урок», множина, що містить чотири геометричні фігури – все це рівно потужні множини. (однакова кількість елементів)
множина букв у слові «урок», множина, що містить чотири геометричні фігури – все це рівно потужні множини. (однакова кількість елементів)
А=  ; В=
; В= 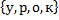 ; С=
; С= 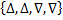
N(А)=4 n(А)=
n(А)=4 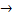 n(В)=
n(В)=
С(С)=4 n(С)=
Тоді множини А,В,С рівно потужні
Якщо між двома множинами можна встановити взаємно однозначну відповідність, то ці множини називаються еквівалентними або рівно потужні.
Позначаються рівно потужні множини: 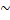
Якщо множина Х рівно потужна множині У, то записують так Х: 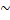 У
У
Властивості для рівно потужних множин:
Рефлективність: Х: 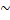 Х (будь-яка множина рівно потужна сама собі)
Х (будь-яка множина рівно потужна сама собі)
Симетричність: х: 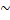 У<=>У
У<=>У 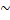 Х
Х
Транзитивність: Х: 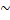 У, У
У, У 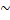 Z<=> Х
Z<=> Х 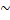 Z
Z
16. Порядкові і кількісні натуральні числа.
Натуральні числа розд. на: порядкові і кількісні
Кількісні натуральні числа
Характер, чисельність скінченної множини і дають відповідь на запитання: « Скільки елементів містить множина?»
Порядкові натуральні числа
Вказують яке місце при лічбі займає той чи інший елемент множини і відповідає на запитання: « Яким по порядку буде той чи інший елемент?»
17.Теоретико-множинний зміст кількісного натурального числа і числа нуль.
Кількісне натуральне число являється властивістю класу скінченних рівно потужних множин.
Кожному класу відповідає єдине натуральне число, кожному числу – єдиний клас рівно потужних множин
Нуль, спочатку означав відсутність числа; він став розглядатися як число лише після введення від’ємних чисел (іноді включають до натуральних чисел)
Число нуль також має теоретико-множинний зміст – воно ставиться в відповідність пустій множині
А= 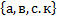 →4 ; А
→4 ; А 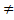 Ø→0
Ø→0
18,Додавання цілих невідємних чисел. Закони додавання.
Сумою ЦНЧ а і в називають число елементів в обєднанні перетинаючи множин А і В
А і В
N(А)=а; n(В)=в
а+в= n(А)+ n(В)= n(А 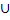 В) → сума завжди існує і єдина
В) → сума завжди існує і єдина
Дія, при якій знаходять суму називається додаванням, а числа, які додаються доданками
Закони додавання:
Комутативний (переставний) а+в=в+а
3+5+2=3+2=5=5+5=10
Асоціативний (сполучний) а+в+с=(а+в)+с=а=(в+с)
17+9+3=(17+3)=9=29
19.Віднімання. Правила віднімання.
Різницею чисел а і в називають число елементів доповнення множини В до множини А
а - в= n(А\В), де n(А)=а і n(В)=в, В А
Різницею чисел а і в називають таке число с, сума якого з числом в = а
а-в=с  а=в+с
а=в+с
Дія за допомогою якої знаходять різницю називається відніманням, а компоненти: зменшуване, від’ємник, різния.
Різниця чисел існує тоді й тільки тоді, коли а  в
в
Вірність даної операції перевіряється додаванням
Якщо різниця існує, то вона єдина.
Щоб дізнатися, на скільки одне число менше чи більше іншого, потрібно від більшого числа відняти менше.
Правила віднімання числа з суми і суми з числа:
1. Щоб відняти число від суми, достатньо відняти його з з одного з доданків і до отриманого результату додати інший доданок.
(10+5)-7=10-7+5=3+5=8
а)якщо а  с , то (а+в)-с= (а-с)+в
с , то (а+в)-с= (а-с)+в
(10+7)-6=7-6+10=1=10=11
б)якщо в  с, то (а+в)-с=(в-с)+а
с, то (а+в)-с=(в-с)+а
2. щоб відняти від числа суму чисел, достатньо відняти від цього числа послідовно доданки
15-(5+3)=15-5-3=10-3=7
Дата: 2018-09-13, просмотров: 786.