Множини – це одне із основних понять сучасної математики, а також інших наук, яке використовується майже в усіх її розділах і якому не даються означення.

Множина належить до певних не визначних понять.

Предмети, або об’єкти, з яких складається задана множина називають її елементами.

Елементи множин позначаються малими літерами латинського алфавіту а,в)

Самі ж множини позначаються великими буквами латинського алфавіту (А,В)

Символ належності 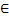 , символ неналежності ȼ

Множину, в якій немає жодного елемента називають порожня множина

Множини бувають скінченні і нескінченні

Злічена множина –це (елементи можна пронумерувати) – може бути скінченною і нескінченною.

Якщо множина складається наприклад з трьох елементів а,в,с, то пишуть А= 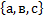(якщо можна перерахувати – фігурні дужки)

Порядок запису елементів порядок істотним не являється.

Якщо множина в складається тільки з елементів множини А, то множину В називають підмножиною множини А    В

Порожня множина є підмножиною будь-якої множини

Множина а є підмножиною самій собі

Якщо елементи множини А є елементами множини В – включення

Дві множини А і В називаються рівними, якщо вони складаються з одних і тих самих елементів

А = 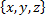 B=

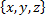
Способи задання множин

1. Задання множин переліком всіх елементів

2. характеристична властивість

3. графіком

4. круги Ейлера

Для задання множин, утвореної з будь-яких елементів, будемо використовувати два такі способи.

В основі обох із них лежать позначення множини за допомогою фігурних дужок.

І спосіб: Задання скінченної множини – це перелік усіх елементів відповідної множини, порядок запису не суттєвий.

ІІ спосіб: ґрунтується на заданні загальної властивості або породжувальної процедури, і запис це так: М= 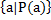(М – множина всіх таких елементів а, для яких виконується властивість Р».

Відношення між множинами

Відношення: множини можуть:

· Не перетинатися тоді А∩В або А∩В = 0

· Перетинатися: А∩В = С

· Розташовуватись одна в одній

Діаграми Ейлера - (круги Ейлера) – це геометричні уявлення множин. Побудова діаграм складається з зображення великого прямокутника, що представляє з себе універсальну множину U, а всередині його – круги (або будь-які інші замкнені фігури), що представляють множини. Фігури повинні перетинатись у найбільш загальному випадку, що вимагається в задачі і повинні бути відповідним чином позначені. Точки, що лежать всередині різних областей діаграми, можуть розглядатись як елементи відповідних множин. Маючи побудовану діаграму, можна заштрихувати певні області для позначення знову створених множин.