Математичні поняття та їх означення
Математика, як і інші науки, вивчає навколишнє середовище, природні та суспільні явища, але вивчає їх лише з особливого буку.
Як сказав Ф. Енгельс: «Математика – це наука про кількісні форми і просторові уявлення реального світу»
Математика, як предмет – абстрактна наука – має складові: (геометрія, алгебра, арифметика)
Означення, об’єм, зміст поняття
Будь-який математичний об’єкт має певні властивості: розрізняють властивості суттєві (істотні) і несуттєві (неістотні).
Властивість вважається суттєвою для об’єкта, якщо вона притаманні цьому об’єкту і без нього він не може існувати.
Несуттєвими властивостями вважаються такі, відсутність яких не впливає на існування об’єктів.
Сукупність всіх взаємопов’язаних суттєвих властивостей об’єкта називають змістом поняття про цей об’єкт.
Об’єм поняття – сукупність всіх об’єктів, які позначені одним терміном
(між об’ємом поняття і його змістом існує зв'язок: чим «більше» об’єм поняття, тим «менше» його зміст і навпаки)
Означення – логічна операція, яка розкриває зміст поняття
(розрізняють явні і неявні означення. Явні означення мають форму рівності, спів падання двох понять, або ототожнюють два поняття)
Неявні означення мають форму спів падання двох понять. Прикладами таких означень є так звані констектуальні (через текст) і остенсивні (показування) означення.
Визначне поняття = визначальному, яке складається з родового поняття + видова відмінність.
Означення побудовані через побудову геометричних об’єктів, які описують означу вальні об’єкти називають генетичним .
Вимоги до означень: (щоб оцінити правильність)
1. Визначне і визначальне поняття повинні бути еквівалентні (повністю співпадати)
2. забороняється порочне коло: не можна визначати поняття саме через себе або визначати його через інше поняття, яке в свою чергу визначається через нього.
3.В означенні мають бути вказані всі властивості, які дозволяють одночасно виділити об’єкти, що належать ообєкту визначального поняття.
4.Відсутність в ньому збитку: не повинно бути вказано зайвих властивостей(нічого зайвого)
5.Необхідно, щоб означувальний об’єкт існував.
Способи задання множин
1. Задання множин переліком всіх елементів
2. характеристична властивість
3. графіком
4. круги Ейлера
Для задання множин, утвореної з будь-яких елементів, будемо використовувати два такі способи.
В основі обох із них лежать позначення множини за допомогою фігурних дужок.
І спосіб: Задання скінченної множини – це перелік усіх елементів відповідної множини, порядок запису не суттєвий.
ІІ спосіб: ґрунтується на заданні загальної властивості або породжувальної процедури, і запис це так: М= 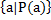 (М – множина всіх таких елементів а, для яких виконується властивість Р».
(М – множина всіх таких елементів а, для яких виконується властивість Р».
Відношення між множинами
Відношення: множини можуть:
· Не перетинатися тоді А∩В або А∩В = 0
· Перетинатися: А∩В = С
· Розташовуватись одна в одній
Діаграми Ейлера - (круги Ейлера) – це геометричні уявлення множин. Побудова діаграм складається з зображення великого прямокутника, що представляє з себе універсальну множину U, а всередині його – круги (або будь-які інші замкнені фігури), що представляють множини. Фігури повинні перетинатись у найбільш загальному випадку, що вимагається в задачі і повинні бути відповідним чином позначені. Точки, що лежать всередині різних областей діаграми, можуть розглядатись як елементи відповідних множин. Маючи побудовану діаграму, можна заштрихувати певні області для позначення знову створених множин.
Відношення еквівалентності
Відношення у множині називається відношенням еквівалентності, якшо воно рефлексивне, симетричне і транзитивне.
А=
R «Бути рівними
В даному відношенні присутні відношення рефлексивності (і на графі петля, пари з рівними компонентами елементами). Присутнє відношення симетричності два елементи з’єднані стрілками (з 2, 2з ) ав парах компоненти міняються місцями. Присутнє відношення транзитивності. Отже робимо висновок: дане відношення є відношенням еквівалентності
Якщо у множині Х задано еквівалентності, то воно розбиває дану множину на підмножини, попарно не перетинаються → називається класи еквівалентності.
Відношення порядку
Відношення R на множині Х, називається відношенням порядку, якщо воно транзитивне і антисиметричне.
Множина із заданим на ній відношенням порядку називається впорядкованою множиною.
Залежно від видів відношень порядку розрізняють і види впорядкованих множин.
14.Поняття Відповідності. Відповідність, обернена даній.
Означення. Відповідністю між елементами двох множин (бінарною відповідністю) називається підмножина декартового добутку ХЧУ.
Множина Х називається множиною відправлення, а множина Y – множиною прибуття відповідності. Разом їх називають базовими множинами відповідності.
15.Взаємнооднозначні відповідності. Рівно потужні множини.
Взаємно однозначними відповідностями називаються відповідності, якщо кожному елементу множини Х відповідає єдиний елемент множини У, і кожний елемент множини У відповідає єдиному елементу множини Х.
У початковій школі поняття взаємно однозначної відповідності використовується неявно: на даному понятті будується лічба предметів, їх порівняння.
Акщо відповідності взаємно однозначні, то кількість елементів відповідних множин рівні.
Приклад: Множина А=  множина букв у слові «урок», множина, що містить чотири геометричні фігури – все це рівно потужні множини. (однакова кількість елементів)
множина букв у слові «урок», множина, що містить чотири геометричні фігури – все це рівно потужні множини. (однакова кількість елементів)
А=  ; В=
; В= 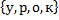 ; С=
; С= 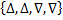
N(А)=4 n(А)=
n(А)=4 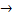 n(В)=
n(В)=
С(С)=4 n(С)=
Тоді множини А,В,С рівно потужні
Якщо між двома множинами можна встановити взаємно однозначну відповідність, то ці множини називаються еквівалентними або рівно потужні.
Позначаються рівно потужні множини: 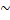
Якщо множина Х рівно потужна множині У, то записують так Х: 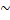 У
У
Властивості для рівно потужних множин:
Рефлективність: Х: 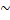 Х (будь-яка множина рівно потужна сама собі)
Х (будь-яка множина рівно потужна сама собі)
Симетричність: х: 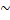 У<=>У
У<=>У 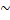 Х
Х
Транзитивність: Х: 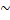 У, У
У, У 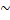 Z<=> Х
Z<=> Х 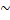 Z
Z
16. Порядкові і кількісні натуральні числа.
Натуральні числа розд. на: порядкові і кількісні
Кількісні натуральні числа
Характер, чисельність скінченної множини і дають відповідь на запитання: « Скільки елементів містить множина?»
Порядкові натуральні числа
Вказують яке місце при лічбі займає той чи інший елемент множини і відповідає на запитання: « Яким по порядку буде той чи інший елемент?»
17.Теоретико-множинний зміст кількісного натурального числа і числа нуль.
Кількісне натуральне число являється властивістю класу скінченних рівно потужних множин.
Кожному класу відповідає єдине натуральне число, кожному числу – єдиний клас рівно потужних множин
Нуль, спочатку означав відсутність числа; він став розглядатися як число лише після введення від’ємних чисел (іноді включають до натуральних чисел)
Число нуль також має теоретико-множинний зміст – воно ставиться в відповідність пустій множині
А= 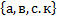 →4 ; А
→4 ; А 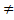 Ø→0
Ø→0
18,Додавання цілих невідємних чисел. Закони додавання.
Сумою ЦНЧ а і в називають число елементів в обєднанні перетинаючи множин А і В
А і В
N(А)=а; n(В)=в
а+в= n(А)+ n(В)= n(А 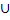 В) → сума завжди існує і єдина
В) → сума завжди існує і єдина
Дія, при якій знаходять суму називається додаванням, а числа, які додаються доданками
Закони додавання:
Комутативний (переставний) а+в=в+а
3+5+2=3+2=5=5+5=10
Асоціативний (сполучний) а+в+с=(а+в)+с=а=(в+с)
17+9+3=(17+3)=9=29
19.Віднімання. Правила віднімання.
Різницею чисел а і в називають число елементів доповнення множини В до множини А
а - в= n(А\В), де n(А)=а і n(В)=в, В А
Різницею чисел а і в називають таке число с, сума якого з числом в = а
а-в=с 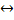 а=в+с
а=в+с
Дія за допомогою якої знаходять різницю називається відніманням, а компоненти: зменшуване, від’ємник, різния.
Різниця чисел існує тоді й тільки тоді, коли а  в
в
Вірність даної операції перевіряється додаванням
Якщо різниця існує, то вона єдина.
Щоб дізнатися, на скільки одне число менше чи більше іншого, потрібно від більшого числа відняти менше.
Правила віднімання числа з суми і суми з числа:
1. Щоб відняти число від суми, достатньо відняти його з з одного з доданків і до отриманого результату додати інший доданок.
(10+5)-7=10-7+5=3+5=8
а)якщо а  с , то (а+в)-с= (а-с)+в
с , то (а+в)-с= (а-с)+в
(10+7)-6=7-6+10=1=10=11
б)якщо в  с, то (а+в)-с=(в-с)+а
с, то (а+в)-с=(в-с)+а
2. щоб відняти від числа суму чисел, достатньо відняти від цього числа послідовно доданки
15-(5+3)=15-5-3=10-3=7
Математичні поняття та їх означення
Математика, як і інші науки, вивчає навколишнє середовище, природні та суспільні явища, але вивчає їх лише з особливого буку.
Як сказав Ф. Енгельс: «Математика – це наука про кількісні форми і просторові уявлення реального світу»
Математика, як предмет – абстрактна наука – має складові: (геометрія, алгебра, арифметика)
Означення, об’єм, зміст поняття
Будь-який математичний об’єкт має певні властивості: розрізняють властивості суттєві (істотні) і несуттєві (неістотні).
Властивість вважається суттєвою для об’єкта, якщо вона притаманні цьому об’єкту і без нього він не може існувати.
Несуттєвими властивостями вважаються такі, відсутність яких не впливає на існування об’єктів.
Сукупність всіх взаємопов’язаних суттєвих властивостей об’єкта називають змістом поняття про цей об’єкт.
Об’єм поняття – сукупність всіх об’єктів, які позначені одним терміном
(між об’ємом поняття і його змістом існує зв'язок: чим «більше» об’єм поняття, тим «менше» його зміст і навпаки)
Означення – логічна операція, яка розкриває зміст поняття
(розрізняють явні і неявні означення. Явні означення мають форму рівності, спів падання двох понять, або ототожнюють два поняття)
Неявні означення мають форму спів падання двох понять. Прикладами таких означень є так звані констектуальні (через текст) і остенсивні (показування) означення.
Визначне поняття = визначальному, яке складається з родового поняття + видова відмінність.
Означення побудовані через побудову геометричних об’єктів, які описують означу вальні об’єкти називають генетичним .
Вимоги до означень: (щоб оцінити правильність)
1. Визначне і визначальне поняття повинні бути еквівалентні (повністю співпадати)
2. забороняється порочне коло: не можна визначати поняття саме через себе або визначати його через інше поняття, яке в свою чергу визначається через нього.
3.В означенні мають бути вказані всі властивості, які дозволяють одночасно виділити об’єкти, що належать ообєкту визначального поняття.
4.Відсутність в ньому збитку: не повинно бути вказано зайвих властивостей(нічого зайвого)
5.Необхідно, щоб означувальний об’єкт існував.
Дата: 2018-09-13, просмотров: 803.