Пусть антагонистическая игра двух участников задана платежной матрицей || a_ij ||, 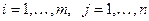 с положительными элементами (условия положительности всегда можно добиться, прибавив ко всем элементам матрицы одно и тоже положительное число) и не имеет седловую точку. Тогда ее решение может быть найдено с помощью ЗЛП. Так, для 1-го игрока достаточно найти min f = x ₁ + x ₂ +…+ x_m при системе ограничений 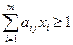, x _i ≥0, для 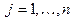, а затем вектор оптимальных смешанных стратегий (p ₁ , p ₂ ,…, p_m), где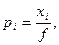 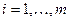. Для второго игрока необходимо найти max f = x ₁ + x ₂ +…+ x_n при системе ограничений 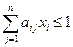, x _i ≥0, для  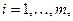а затем вектор оптимальных смешанных стратегий (p ₁ , p ₂ ,…, p_n), где   .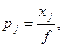

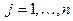Пример задачи по теории игр, решаемой симплексным методом

Задача. Первый и второй игроки одновременно и независимо друг от друга показывают один, два или три пальца. Выигрыш или проигрыш (в денежных единицах) равен общему количеству показанных пальцев. Если это количество четное, то выигрывает первый игрок, а второй ему платит. Если же оно нечетное, то выигрывает второй игрок, а первый ему платит. Найти оптимальные стратегии каждого игрока.

Экономико-математическая модель

 У каждого игрока имеется по три стратегии: показать один, два или три пальца. В соответствии с этим платежная матрица будет выглядеть следующим образом:

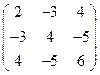
Выберем минимальные значения в каждой строке, а затем из них найдем максимальное. Это даст нам нижнюю цену игры. Она равна -3. Выберем максимальные значения в каждом столбце, а затем из них найдем минимальное. Получим верхнюю цену игры. Она равна 4. Так как нижняя цена игры не совпадает с верхней, то решение будем искать в смешанных стратегиях. Прибавляя ко всем элементам матрицы число, равное 5, перейдем к матрицы модифицированной игры:

,

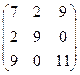которой соответствует задача линейного программирования для 1 игрока:

 min f(x₁, x₂, x₃) =x₁+x₂+x₃

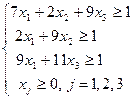
и задача линейного программирования для 2 игрока:

max f(x₁, x₂, x₃) =x₁+x₂+x₃

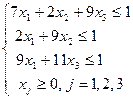
Решение.

Воспользовавшись симплексным методом, получим решения обеих задач, как описано ранее. Результаты приведены на рисунке.

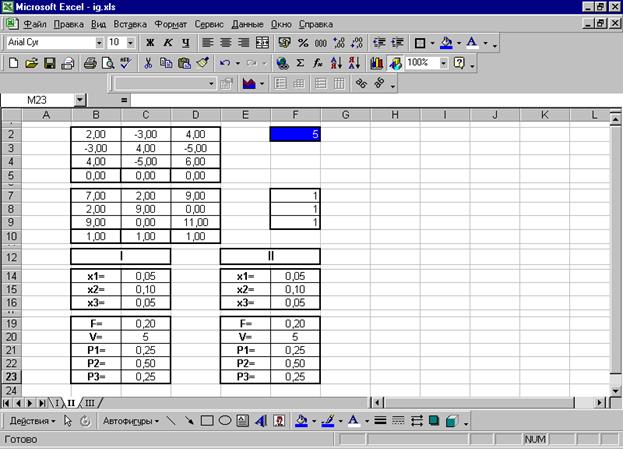
Таким образом, оптимальная смешанная стратегия 1-го игрока совпадает с оптимальной смешанной стратегией 2-го игрока и равна (0,25;0,5;0,25).

Задачи для самостоятельного решения

1. Найти оптимальную стратегию 1-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:

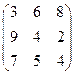
2. Найти оптимальную стратегию 2-го игрока для игры двух участников с нулевой суммой путем сведения ее к задаче линейного программирования, если задана платежная матрица:

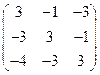
3. Найти оптимальные стратегии игроков для игры двух участников с нулевой суммой, если задана платежная матрица:

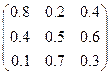
4. Найдите оптимальные стратегии игроков в известной игре «камень, ножницы, бумага».