Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении.
Выбор оптимального управленческого поведения в конкретной ситуации связан с проведением экономико-математического моделирования и решением задачи оптимального программирования, в простейшем случае — задачи линейного программирования.
В наиболее общем виде задача (модель) линейного программирования записывается следующим образом: требуется найти экстремум (максимум или минимум) линейной целевой функции: f ( x1, х2,…, хn) = c1х1+ c2 х2+…+ cn х n
при ограничениях:
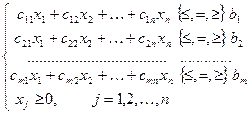
где ci , j , bi (i=1,2,…,m; j=1,2,…,n) — заданные постоянные величины.
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (система ограничений задачи противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи и (или) разработанной ЭММ. Например, имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно, и некоторые существенные ограничения в ней отсутствуют.
Пример задачи линейного программирования
Задача линейного программирования в том или ином виде интерпретируется как задача об оптимальном использовании ограниченных производственных ресурсов.
Задача . Предприятие выпускает продукцию четырех видов П1, П2, П3, П4 с использованием для этого ресурсов, виды и нормы расхода по которым, а также уровень получаемой от их реализации прибыли приведены в таблице. Составьте оптимальный план производства продукции, дающий максимальную прибыль.
| Вид ресурса | Вид продукции | Запас ресурса | |||
| П1 | П2 | П3 | П4 | ||
| Трудовые | 1 | 1 | 1 | 1 | 16 |
| Сырье | 6 | 5 | 4 | 3 | 110 |
| Оборудование | 4 | 6 | 10 | 13 | 100 |
| Прибыль | 60 | 70 | 120 | 130 | |
Экономико-математическая модель:
Введём необходимые обозначения: пусть xj (j=1,2,3,4) – объемы каждого вида продукции. Тогда ЭММ задачи запишется следующим образом:
max f(x1, x2, x3, x4) =60x1+70x2+120x3+130x4,
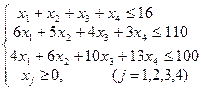
Решение.
1. Создадим форму для ввода условий задачи. Для этого запустим Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Создадим текстовую форму – таблицу для ввода условий задачи.
2. Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Значения компонент вектора X=(x1, x2, x3, x4) поместим в ячейках ВЗ:ЕЗ, оптимальное значение целевой функции – в ячейку F4.
3. Введем исходные данные задачи в созданную форму-таблицу:
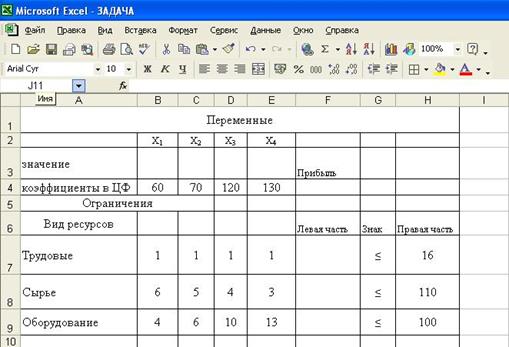
4.Введем зависимость для целевой функции:
· установить курсор в ячейку F4.
· кликнуть по кнопке Мастер функций, расположенной на панели инструментов.
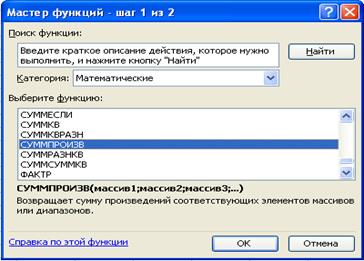
· на экране появляется диалоговое окно Мастер функций – шаг 1 из 2.
· выбрать категорию Математические;
· выбрать функцию СУММПРОИЗВ
· на экране появляется диалоговое окно СУММПРОИЗВ;
· в строку Массив 1 введем В$3:Е$3;
· в строку Массив 2 введем В4:Е4;
· кликнуть по кнопке ОК. На экране в ячейку F4 введена функция.
5. Ввести зависимости для ограничений:
· курсор в ячейку F4; кнопка Копировать;
· курсор в ячейку F7; кнопка Вставить;
· курсор в ячейку F8; кнопка Вставить;
· курсор в ячейку F9; кнопка Вставить.
В строке Меню установить указатель мыши на имя Сервис. В развернутом меню выбрать команду Поиск решения.
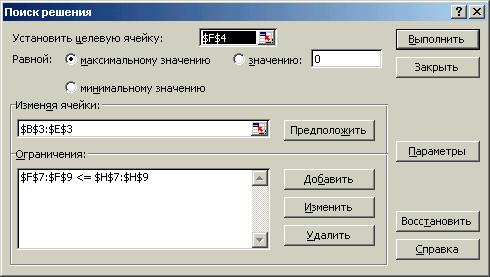
6. Назначим целевую функцию (установим целевую ячейку):
· курсор в строку Установить целевую ячейку;
· введем адрес ячейки $F$4;
· введем направление целевой функции в зависимости от условия задачи – Максимальному значению;
· курсор в строку Изменяя ячейки;
· введем адреса искомых переменных В$3:E$3.
7. Введем ограничения:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адрес $F$7: $F$9 (или укажем на листе, т.е. щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу, выделить ячейки F7:F9, нажать клавишу F 4, при этом ссылка станет абсолютной $F$7: $F$9, щелкнуть на красной стрелке и вернуться в блок Поиска решения, при этом нужный адрес будет введен);
· выберем знак ограничения <=;
· в строке Ограничения введем адрес $Н$7: $Н$9;
· после введения ограничения кнопка ОК.
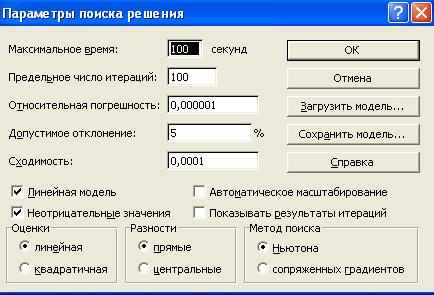
8. Введем параметры для решения ЗЛП:
· в диалоговом окне Поиск решения кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения;
· кнопка ОК. На экране диалоговое окно Поиск решения;
· кнопку Выполнить.
· в диалоговом окно Результаты поиска решения
· выбрать Сохранить найденное решение
· кнопка OK
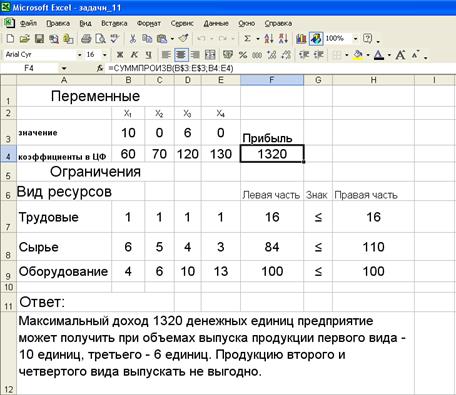
На экране представлена исходная таблица с заполненными ячейками ВЗ:ЕЗ для значений X и ячейка F4 с максимальным значением целевой функции. Введем экономическую интерпретацию полученных результатов: «Максимальный доход 1320 денежных единиц предприятие может получить при объемах выпуска продукции первого вида – 10 единиц, третьего вида – 6 единиц. Продукцию второго и четвертого вида выпускать не выгодно.»
Дата: 2019-12-10, просмотров: 402.