Ниже приводятся примеры специальных ЗЛП – транспортной задачи и задачи о назначениях, которая интерпретируется как частный случай транспортной задачи. Задача о назначениях рассматривается, как пример задачи дискретной оптимизации.
Примеры задач транспортного типа
Задача . Перед менеджером нефтяной компании «Магнум» стоит задача создания схемы поставки нефтепродуктов от четырех нефтеперерабатывающих комплексов компании к пяти регионам страны. Одним из основных условий поставленной задачи является минимизация стоимости перевозок, при этом все мощности нефтеперерабатывающих комплексов должны бьть реализованы и все потребности регионов должны быть удовлетворены.
Мощности поставщиков и мощности потребителей, а также стоимость перевозок нефтепродуктов представлены в следующей таблице (в условных единицах).
| Мощности поставщиков | Мощности потребителей | ||||
| 600 | 400 | 700 | 500 | 1000 | |
| 700 | 4 | 8 | 5 | 1 | 6 |
| 800 | 3 | 5 | 2 | 3 | 4 |
| 900 | 2 | 6 | 5 | 4 | 3 |
| 800 | 1 | 4 | 3 | 5 | 3 |
Решение.
В данном случае мощности поставщиков нефтепродуктов и потребности регионов в них совпадают, т.е. имеем дело с закрытой моделью транспортной задачи.
Ввод условий задачи состоит из следующих основных этапов.
1. Создание формы для решения задачи.
2. Ввод граничных условий.
3. Ввод исходных данных.
4. Назначение целевой функции.
5. Ввод зависимостей из математической модели.
6. Ввод ограничений.
7. Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
1. Создание формы для решения задачи предполагает создание матрицы перевозок. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:F6 заполняется значением 1. Таким образом, резервируется место, где после решения задачи будет находиться распределение поставок, обеспечивающее минимальные затраты на перевозку груза (нефтепродуктов).
2. Ввод граничных условий.
Введение условия реализации мощностей поставщиков, т.е.
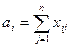
где ai – мощность i -го поставщика;
xi , j – объем поставки груза от i-го поставщика к j-му потребителю;
п – количество потребителей.
Для этого необходимо выполнить следующие операции:
· курсор в ячейку АЗ;
· кнопка Автосумма;
· выделить необходимые для суммирования ячейки ВЗ:FЗ;
· нажать ENTER – подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
· курсор в АЗ;
· кнопка Копировать;
· выделить ячейки А4:А6;
· кнопка Вставить.
Введение условия удовлетворения запросов потребителей, т.е.
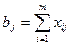
где bj – мощность j -го потребителя;
т – количество поставщиков.
Для этого необходимо выполнить следующие операции:
· курсор в В7;
· кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;
· ЕNTER – подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек С7:F7, или же:
· курсор в В7;
· кнопка Копировать;
· выделить С7:F7;
· кнопка Вставить.
Таким образом, введены ограничения для всех поставщиков и всех потребителей.
3. Ввод исходных данных.
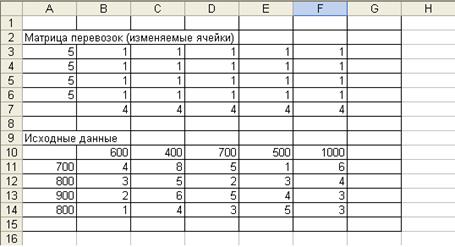
В конкретном примере осуществляется ввод мощностей четырех нефтеперерабатывающих предприятий (ячейки А11:А14), потребности регионов в их продукции (В10: F 10), а также удельные затраты по доставке нефтепродуктов от конкретного поставщика потребителю (блок В11: F 14).
4. Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей минимальным суммарным затратам на доставку груза, необходимо в определенную ячейку ввести формулу для ее вычисления:
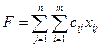
где cij – стоимость доставки единицы груза от i -го поставщика к j -му потребителю;
х ij - объем поставки груза от i-го поставщика к j-му потребителю.
Для этого:
· курсор в ячейку В15. В данную ячейку будет помещаться значение целевой функции после решения задачи;
· кнопка Мастер функций;
На экране появится диалоговое окно Мастер функции шаг - 1 из 2
· выбрать категорию Математические;
· выбрать функцию СУММПРОИЗВ;
В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11: F 14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ: F 6). Для этого:
· в строку Массив 1 ввести В11:F14;
· в строку Массив 2 ввести ВЗ:F6;
· кнопка ОК.
В поле ячейки В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (число 77 в данной задаче).
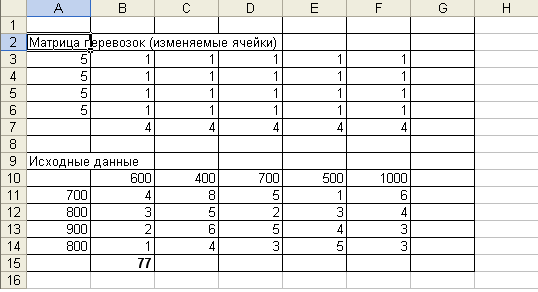
5. Ввод зависимостей из математической модели:
· выбрать Сервис ® Поиск решения;
· курсор в Установить целевую ячейку;
· ввести (выбрать) адрес $В$15.
Таким образом, производится указание ячейки, куда при решении задачи помещается значение целевой функции.
Или:
· поставить курсор в В15
· выбрать Сервис ® Поиск решения.
При этом осуществится автоматический ввод адреса $В$15 в поле адреса целевой ячейки;
· установить направление изменения целевой функции: минимальному значению.
Ввести адреса изменяемых ячеек ВЗ:F6. Для этого:
· щелкнуть в поле Изменяя ячейки;
· ввести адреса $В$3:$F$6 (или укажем на листе).
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие реализации мощностей всех поставщиков. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;
· кнопка OK
На экране появится диалоговое окно Поиск решения с введённым условием.
Далее вводится ограничение, которое реализует условие удовлетворения мощностей всех потребителей. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$F$7;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $В$10:$F$10;
· кнопка OK
6. Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
· кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения:
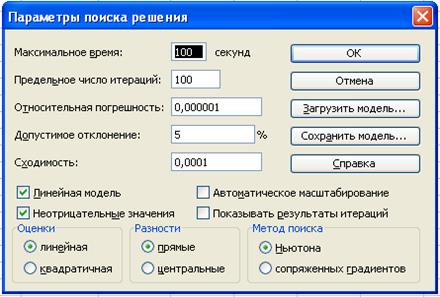
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения, так как объемы поставок груза отрицательной величиной быть не могут;;
· кнопка ОК.
· на экране появится диалоговое окно Поиск решения;
· кнопка Выполнить.
7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения
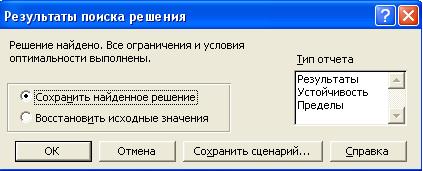
· В окне Тип отчета выбрать интересующий вид отчета.
· кнопка ОК.
Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
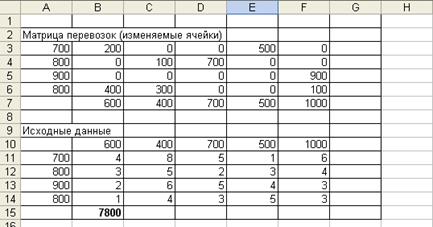
При нажатии Лист 1 происходит возврат в программу к исходным данным.
В матрице перевозок содержатся оптимальные объемы поставок грузов от поставщика потребителям, дающие минимум затрат на доставку. Значение целевой функции содержится в ячейке В15 и для конкретной задачи равно 7800. Из вышеизложенного можно сделать следующий вывод: минимум затрат на доставку нефтепродуктов, равный 7800 условных денежных единиц, будет обеспечен при следующем плане поставок:
1) от первого поставщика первому потребителю в объеме 2 (единиц и четвертому в объеме 500 единиц (условных);
2) от второго поставщика второму потребителю в объеме 18 единиц и третьему потребителю в объеме 700 единиц (условных);
3) от третьего поставщика пятому потребителю в объеме 900 единиц (условных);
4) от четвертого поставщика первому потребителю в объеме 400 единиц и второму потребителю в объеме 300 единиц (условных).
При данной схеме поставок мощности всех поставщиков будут реализованы и спросы всех потребителей будут удовлетворены.
Рассмотрим задачу о назначениях, которая в этом случае интерпретируется и реализуется как частный случай транспортной задачи.
Задача. На коммерческом предприятии имеется т работников А1, А2, ... А i , …Ат, каждый из которых может выполнять одну из имеющихся т видов работ: В1, В2, ... В j ,… В m . Известно, что один и тот же работник может выполнять различные виды работ с разной производительностью труда (cij) в зависимости от опыта работы, квалификации, индивидуальны особенностей. В связи с этим возникает проблема распределений работников по должностям таким образом, чтобы производительность труда в коллективе была максимальной.
Экономико-математическая модель:
Обозначим через xij назначение i-го работника на j-должность. Так как количество работников равно количеству должностей и один работник может занимать только одну должность, то х ij может принимать только два значения: 1 (если работник назначается на данную должность) или 0 (если не назначается). Тогда суммарная производительность труда работников (целевая функция) имеет следующий вид:
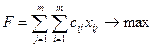
при ограничениях:
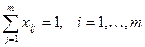
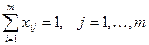
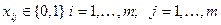
Умножая целевую функцию на -1, задача распределения по должностям может быть приведена к транспортной задаче, в которой объем запасов каждого поставщика и объем потребностей каждого потребителя равны 1.
Задача . Перед менеджером фирмы «Стар» стоит задача распределения четырех работников по вакантным должностям по условиям результатов контролых испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.
Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.
| Работники | Производительность труда работников по должностям | |||
| В1 | В2 | В3 | В4 | |
| А1 | 3 | 1 | 5 | 2 |
| А2 | 2 | 4 | 8 | 6 |
| А3 | 8 | 2 | 7 | 6 |
| А4 | 4 | 3 | 5 | 1 |
Решение.
Ввод условий задачи состоит из следующих основных этапов:
1. Создание формы для решения задачи.
2. Ввод граничных условий.
3. Ввод исходных данных.
4. Назначение целевой функции.
5. Ввод зависимостей из математической модели.
6. Ввод ограничений.
7. Просмотр результатов и печать отчета.
Рассмотрим более подробно каждый из этих этапов.
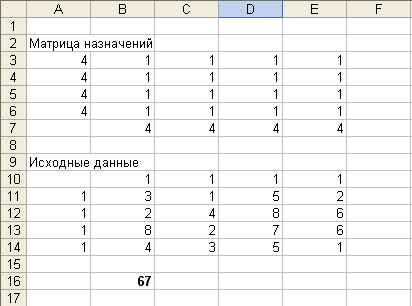
1. Создание формы для решения задачи предполагает создание матрицы назначений по должностям. Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек ВЗ:Е6 вводятся «1». Таким образом, резервируется место, где после решения задачи будет находиться распределение рабочих по должностям, обеспечивающее максимальную производительность труда.
2. Ввод граничных условий.
Введение условия назначения работника только на одну должность, т.е.
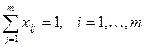 ,
,
где х ij – назначение i-го работника на j-ую должность;
т – количество вакантных должностей
Для этого необходимо выполнить следующие операции:
· курсор в ячейку АЗ;
· кнопка Автосумма;
· выделить необходимые для суммирования ячейки ВЗ:EЗ;
· нажать ENTER – подтверждение ввода формулы для суммирования.
Аналогичные действия выполнить для ячеек А4, А5, А6, т.е. ввести условия реализации мощностей всех поставщиков (для всех строк). Эти действия можно реализовать иначе:
· курсор в АЗ;
· кнопка Копировать;
· выделить ячейки А4:А6;
· кнопка Вставить.
Введение условия заполнения вакантной должности, т.е.
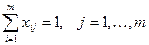
Для этого необходимо выполнить следующие операции:
· курсор в В7;
· кнопка Автосумма. При этом автоматически выделятся весь столбец ВЗ:В6;
· ЕNTER – подтверждение суммирования показателей выделенного столбца.
Последовательность этих действий выполнить для ячеек С7:F7, или же:
· курсор в В7;
· кнопка Копировать;
· выделить С7:F7;
· кнопка Вставить.
Таким образом, введены ограничения по назначению работника только на одну должность и условию заполнения всех вакантных мест.
3. Ввод исходных данных.
В конкретном примере осуществляется ввод условной мощности работника фирмы (в ячейки А11:А14 вводится «1»), потребности в заполнении вакантной должности («1» - в В10:Е10), ввод производительности труда конкретного работника при проведении контрольных испытаний по каждой должности (блок В11:Е14).
4. Назначение целевой функции.
Для вычисления значения целевой функции, соответствующей максимальной суммарной производительности труда, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:
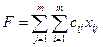
где cij – производительность труда i-го работника при занятии j-й должности;
х ij – назначение i -го работника на j-должность. Для этого:
· курсор в ячейку В16. В данную ячейку будет помещаться значение целевой функции после решения задачи;
· кнопка Мастер функций;
На экране появится диалоговое окно Мастер функции шаг - 1 из 2
· выбрать на категорию Математические;
· выбрать функцию СУММПРОИЗВ;
В задаче целевая функция представляет собой произведение удельных затрат на доставку груза (расположенных в блоке ячеек В11: F 14) и объемов поставок для каждого потребителя (содержимое ячеек ВЗ: F 6). Для этого:
· в строку Массив 1 ввести В11:F14;
· в строку Массив 2 ввести ВЗ:F6;
· кнопка ОК – подтверждение окончания ввода адресов массивов
В поле ячейки В16 появится некоторое числовое значение равное произведению «1» на производительность каждого работника на конкретной должности (число 67 в данной задаче).
5. Ввод зависимостей из математической модели.
Для осуществления этого этапа необходимо выполнить следующий перечень операций:
· поставить курсор в В16
· выбрать Сервис ® Поиск решения.
При этом осуществится автоматический ввод адреса $В$16 в поле адреса целевой ячейки;
· установить направление изменения целевой функции: минимальному значению.
Ввести адреса изменяемых ячеек ВЗ:E6. Для этого:
· щелкнуть в поле Изменяя ячейки;
· ввести адреса $В$3:$E$6 (или укажем на листе).
Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие назначения работника только на одну должность. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $А$3:$А$6;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $А$11:$А$14;
· кнопка OK
На экране появится диалоговое окно Поиск решения с введённым условием.
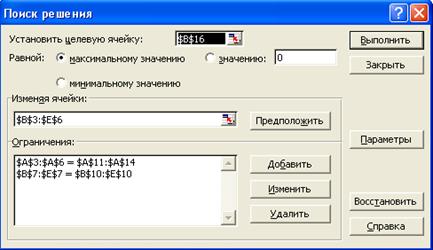
Далее вводится ограничение, которое реализует условие заполнения вакантной должности. Для этого:
· кнопка Добавить. Появляется диалоговое окно Добавление ограничения;
· в строке Ссылка на ячейку введем адреса (или укажем на листе) $В$7:$E$7;
· выберем знак ограничения =;
· в строке Ограничение введем адреса (или укажем на листе) $В$10:$E$10;
· кнопка OK
6. Ввод ограничений.
Далее необходимо установить ограничения на решение задачи. Для этого:
· кнопка Параметры.
· на экране диалоговое окно Параметры поиска решения:
· установим флажки:
ü Линейная модель (это обеспечит применение симплекс-метода)
ü Неотрицательные значения, так как значение работника на должность принимает значение «1» или «0» , т.е. отрицательной величиной быть не может;
· кнопка ОК.
· кнопка Выполнить.
7. Просмотр результатов и печать отчета. После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения
· В окне Тип отчета выбрать интересующий вид отчета.
· кнопка ОК.
Внизу страницы экрана содержится сообщение Отчет по результатам 1. Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.
При нажатии Лист 1 происходит возврат в программу, к исходным данным.
В Матрице назначений содержится схема распределения работников по должностям (1 – назначен, 0 – не назначен), дающая максимальную суммарную производительность труда, Значение целевой функции содержится в ячейке В16 и для конкретной задачи равно 22.
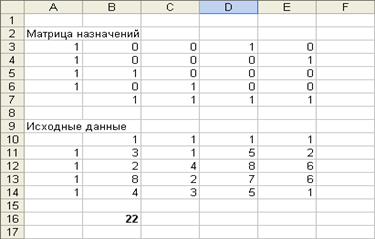
Вывод: максимум производительности труда, равный 22 условных единицы, будет достигнут при назначении:
1. первого работника на должность В3 (содержимое ячейки D З = 1);
2. второго работника на должность В4 (Е4=1);
3. третьего работника на должность В1 (В5=1);
4. четвертого работника на должность В2 (С6=1).
Задачи для самостоятельного решения
1. Решите транспортную задачу, определив минимальную стоимость перевозки грузов
| Мощности поставщиков | Мощности потребителей | |||
| 22 | 34 | 41 | 20 | |
| 31 | 10 | 7 | 6 | 8 |
| 48 | 5 | 6 | 5 | 4 |
| 38 | 8 | 7 | 6 | 7 |
2. Перед менеджером стоит задача распределения четырех работников по вакантным должностям по условиям результатов контрольных испытаний. Производительность труда по отдельным видам работ, показанная каждым из работников, приведена в таблице.
Одним из основных условий поставленной задачи является максимизация производительности труда в коллективе при условии, что каждый работник может быть назначен только на одну работу.
| Работники | Производительность труда работников по должностям | |||
| В1 | В2 | В3 | В4 | |
| А1 | 9 | 6 | 5 | 8 |
| А2 | 4 | 8 | 6 | 2 |
| А3 | 6 | 7 | 9 | 4 |
| А4 | 2 | 7 | 3 | 1 |
Чему равен максимум производительности труда?
3. Для строительства 4 дорог необходим гравий в количестве 130, 220, 60 и 70 единиц, который может быть поставлен из 3 карьеров, запасы которых составляют120,280 и 160 единиц соответственно, а тарифы перевозок представлены таблицей
| 1 | 7 | 9 | 5 |
| 4 | 2 | 6 | 8 |
| 3 | 7 | 1 | 2 |
Дата: 2019-12-10, просмотров: 433.