Для определения перемещения точки В стержня необходимо помнить, что смещение сечения зависит от деформации не всего бруса, а лишь некоторой его части между сечением и заделкой. Так в нашем случае перемещение точки В равно суммарному изменению длины участков ВС и CD:
.
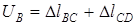При вычислении абсолютных деформаций участков моно применить принцип независимости действия сил и формулы (1.5) и (1.9).
На участок CD как внешние силы действуют: 2Р – растягивающая и Т2 – сжимающая.
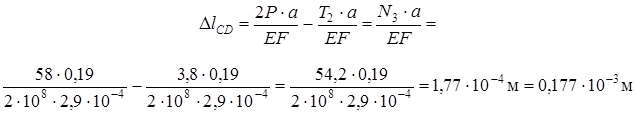
На участок СВ как внешняя сила действует Р = 29 кН и равномерно распределенная нагрузка t = 20 кН/м.
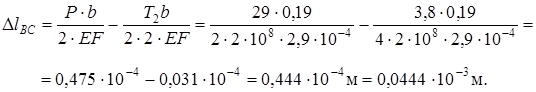
Таким образом,
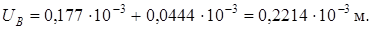
Точка В перемещается вверх.
Вопросы для самопроверки
1. Что такое центральное растяжение и сжатие?
2. Что понимается под продольной силой в брусе, и каким способом она определяется?
3. Какое правило знаков принято при определении продольной силы? Какова размерность продольной силы?
4. Что такое эпюра продольной силы? Как она строится и с какой целью?
5. Что такое напряжение? Чем определяется знак напряжения? Какова размерность напряжения? Какие факторы влияют на величину напряжения?
6. Напишите условие прочности при растяжении или сжатии.
7. Что называется абсолютной (полной) продольной деформацией? Напишите формулу абсолютной деформации.
8. Как формулируется закон Гука? Напишите формулы, выражающие закон Гука, для относительной и абсолютной продольной деформации бруса.
II. КРУЧЕНИЕ СТЕРЖНЕЙ КРУГЛОГО СЕЧЕНИЯ
Кручением называется такой случай деформации стержня, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – момент относительно продольной оси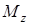 
, который называется крутящим моментом 
.
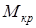Стержни, работающие на кручение, называются валами. Кручение валов часто сопровождается изгибом (см. задачу № 7). На рис. 3 показана часть вала, подверженная кручению без изгиба. Силы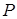 
с помощью рычагов создают внешние крутящие 
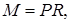не вызывая изгиба, так как в месте прикрепления рычагов размещаются опоры, препятствующие перемещениям направленным перпендикулярно оси вала, но не препятствующим повороту поперечных сечений относительно оси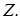 
Для определения внутренних усилий, возникающих в поперечных сечениях вала под действием внешних моментов, используется метод сечений.
Правило знаков: крутящий момент считается положительным, если при взгляде на поперечное сечение оставшейся части он виден вращающим по ходу часовой стрелки.
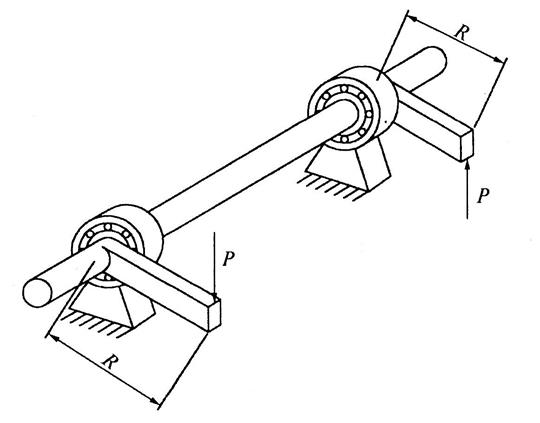
Рассмотрим случай, когда все внешние моменты уравновешены и действуют в плоскостях, перпендикулярных оси стержня (рис. 4,а).
– М1 – М2 + М3 – М4 = 0 2.1)
Для определения крутящих моментов в каком-либо сечении, например I–I, мысленно разрежем вал по этому сечению на две части и приложим к каждой части крутящие моменты М z. Величину крутящего момента можно найти из условия равновесия любой из отсеченных частей. Для этого необходимо приравнять нулю сумму моментов относительно продольной оси стержня.
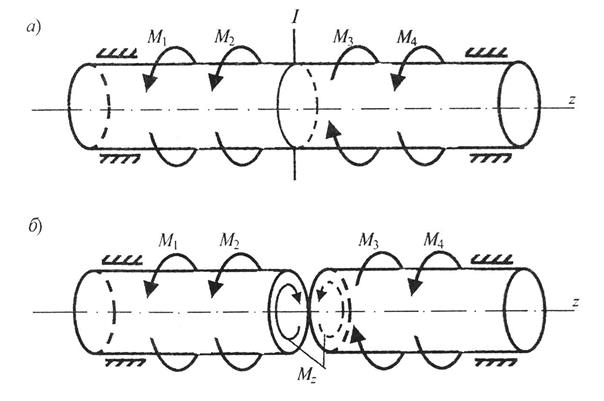
Так, например, для случая, показанного на рис. 4,б, из уравнения равновесия левой части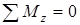 
находим
-М1 – М2 + М z =0,
откуда М z = М1 + М2 . (2.2)
Для случая, когда берется равновесие правой части, имеем
М z – М3 + М4 =0.
Следовательно М z = М3 – М4. (2.3)
Легко заметить, что оба момента М z равны между собой. Это видно из равенства (2.1), откуда
М1 + М2 = М3 – М4.
В общем случае вместо уравнения (2.2) или соответственно уравнения (2.3) можно было бы написать:
М z = å Млев,
М z = å Мпр.
Таким образом, крутящий момент М z в сечении стержня численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.
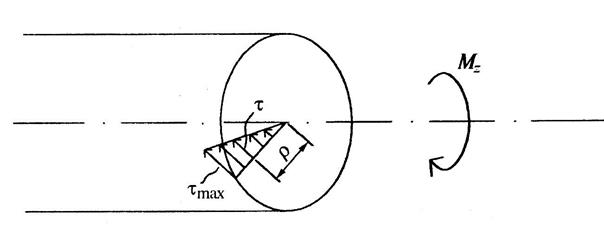
В круглом или трубчатом поперечном сечении скручиваемого стержня возникают касательные напряжения, которые определяются по формуле
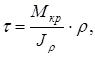(2.4)
где Мкр – крутящий момент в сечении; J r – полярный момент инерции сечения; r – расстояние от оси стержня до точки поперечного сечения в окрестности которой определяется напряжение.
Касательные напряжения направлены перпендикулярно радиусу в сторону соответствующую направлению Мкр (рис. 5).
Для круглого сечения
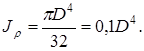(2.5)
Для трубчатого сечения
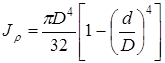. (2.6)
где D и d – диаметры внешней и внутренней окружности.
Максимального значения напряжения достигают в крайних точках сечения у поверхности вала.
При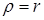 
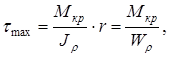(2.7)
где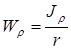 
– полярный момент сопротивления круглого сечения, r – радиус вала.
Для круглого сечения
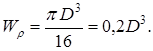(2.8)
Для трубчатого сечения
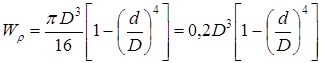. (2.9)
Деформация при кручении валов состоит во взаимном повороте двух сечений относительно продольной оси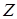 
. Два сечения в начале и конце участка с постоянными моментами поворачиваются на угол
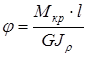, (2.10)
здесь l – длина участка вала; GJ r – жесткость при кручении; G – модуль сдвига.
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания Q
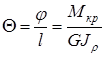. (2.11)
Условие прочности при кручении имеет вид
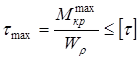, (2.12)
где [t] – допускаемое касательное напряжение.
При проектировании диаметр вала определяется из условий прочности и жесткости
Для круглого сечения
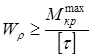
и
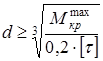. (2.13)
Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого значения угла закручивания на единицу длины [Q]. Условие жесткости при кручении
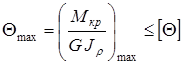. (2.14)
Допускаемый угол закручивания [Q] на погонный метр длины, принимается для разных конструкций и видов нагрузки в пределах не более 2°/м.
Отсюда для круглого поперечного сечения
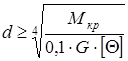. (2.15)
Из двух значений, определяемых по (2.13) и (2.15), выбирается большее и округляется в соответствии с ГОСТ.
Пример 2. Стальной вал переменного сечения (G = 8×104 МПа;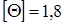 
о/м, [t] = 120 МПа), испытывает кручение от приложенных к нему трех известных моментов М1, М2, М3 и одного неизвестного 
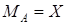(рис. 6, а). Схема получается из задания задачи № 2, если условно принять сечение Е неподвижным.
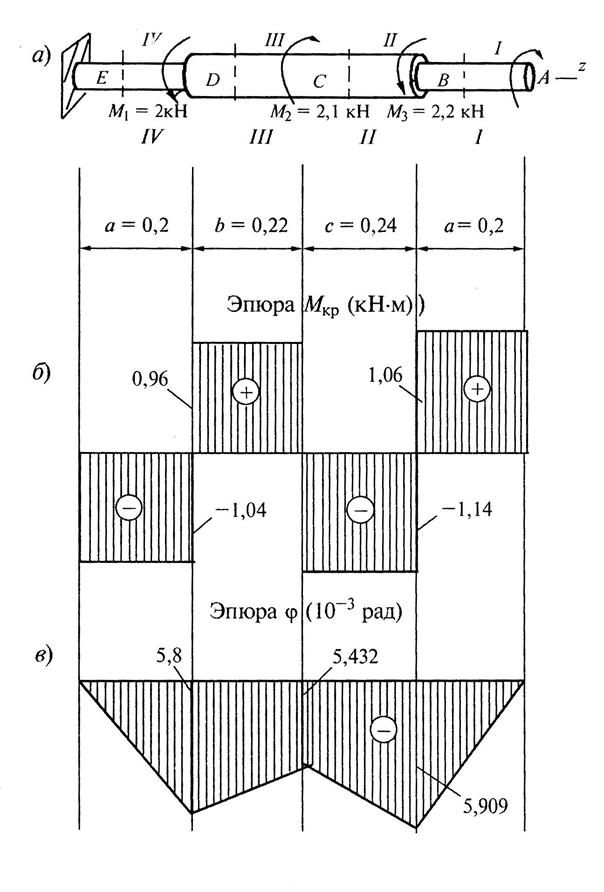
Требуется:
1) установить при каком значении момента Х угол поворота правого концевого сечения вала равен нулю;
2) для найденного значения Х построить эпюру крутящих моментов;
3) определить размеры поперечного сечения вала из условий прочности и жесткости, приняв, что участки длиною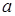 
– имеют диаметр d1, а 
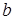и 
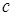– диаметр d2, и 
;
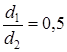4) показать распределение касательных напряжений в поперечных сечениях;
5) построить эпюру углов закручивания.
Решение
Дата: 2019-12-22, просмотров: 282.
