и нормального напряжения s

Для этой цели воспользуемся методом сечений.

I участок (А – В) 0 м Ј z₁ Ј 0,15 м

Проведем сечение 1–1 на расстоянии z₁ от начала координат (точка А), отбросим нижнюю часть (рис.2). Рассмотрим равновесие верхней отсеченной части. На нее действует только внешняя сила P и продольная сила 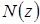, показанная в положительном направлении, которая учитывает воздействие нижней отброшенной части (рис. 2,б).

Составим уравнение равновесия и выразим продольную силу, действующую на первом участке:

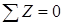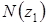;    – Р = 0;  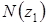    = Р = 29 кН.

Для нормального напряжения (при F₁ = F = const):

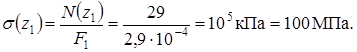
Полученные величины продольной силы 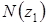 и нормального напряжения  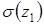не меняются по всей длине первого участка.

II участок (B – C) 0,15 м Ј z₂ Ј0, 34 м

Аналогично предыдущему проведем сечение 2–2 на расстоянии z₂ от свободного конца бруса, в пределах II-го участка (рис. 2,в). Для верхней части составим уравнение равновесия .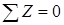

В это уравнение войдут: сосредоточенная сила Р= 29 кН, равнодействующая продольной распределенной нагрузки 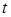 по длине отсеченной части второго участка 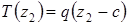, а также сила  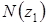, показанная в положительном направлении.

При этом уравнение равновесия примет вид:

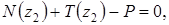
отсюда 

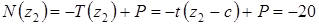
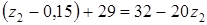 кН.

Учитывая постоянство площади поперечного сечения на втором участке, выражение для нормального напряжения может быть записано таким образом:                                            

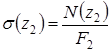
Анализируя полученные выражения, видим, что величины продольной силы  и 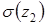 имеют линейную зависимость от ординаты z₂. Поэтому для построения эпюр достаточно определить их значения в начале и конце участка:

при z₂ = 0,15:    N(0,15) = 32 – 2 × 0,15 = 29 кН;

                            s(0,15) = 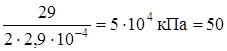 МПа;

при z₂ = 0,34:    N(0,34) = 32 – 20 × 0,34 = 25,2 кН;

s(0,34) = .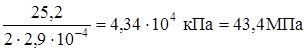

Проводим сечение 3–3 на расстоянии z₃ от свободного конца бруса, в пределах III-го участка (рис. 2,г).

III участок (C – D) 0,34 м Ј z₃ Ј 0,53 м

Уравнение равновесия принимает вид:

:      

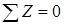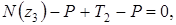
Выразив 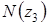, получаем:

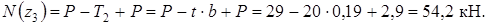
Выражение для нормального напряжения может быть записано таким образом: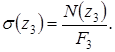

Подставив числовые значения в приведенную формулу, получаем:

.

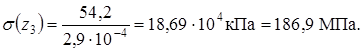По полученным значениям строим эпюры N_z и s _z (рис. 2,д,е)_. Необходимым условием правильности построения этих графиков является выполнение следующих требований:

– растягивающие усилия N_z  и нормальные напряжения s _z  со знаком “+” откладываем влево от базисной линии 0–0, отрицательные вправо;

– если нагрузка равномерно распределена по длине участка, то эпюра ограничена наклонной линией;

– скачок в эпюре N должен находиться в точке приложения сосредоточенного усилия и быть равным по величине значению этой силы;

– скачки в эпюре s  должны совпадать с точками приложения внешней силы Р и изменения площади поперечного сечения бруса.