РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

21/1/14 Одобрено кафедрой
«Сопротивление материалов
и строительная механика»
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методические указания к выполнению
Контрольной работы № 1
для студентов III курса
Специальностей:
Локомотивы (Т)
Вагоны (В)
Подъемно-транспортные, строительные, дорожные машины и оборудование (СМ)
Электрический транспорт железных дорог (ЭПС)
Москва – 2003
Рецензент: д.т.н.Павлов Ю.А., профессор кафедры «Здания и сооружения на транспорте»
Ó Российский государственный открытый технический
университет путей сообщения, 2003
ОБЩИЕ ПОЛОЖЕНИЯ
Примеры решения задач, приведенные в данном методическом указании, относятся к двум видам простого сопротивления материалов: растяжению-сжатию и кручению.
В целях более глубокого понимания предлагаемых решений студентам необходимо изучить по литературным источникам соответствующие разделы курса «Сопротивление материалов». Особое внимание следует обратить на решения задач приведенные в учебниках. Кроме того, следует самостоятельно изучить раздел курса, посвященный определению геометрических характеристик плоских сечений.
К выполняемым контрольным работам предъявляется следующие требования. Каждая контрольная работа должна состоять из расчетов и пояснений к ним. Расчетные схемы и чертежи эпюр можно выполнять в тетради, но лучше это делать на отдельных листах миллиметровой бумаги.
Все схемы и чертежи должны быть выполнены карандашом и в масштабе, удобном для изображения. Схемы и чертежи должны иметь необходимые числовые размеры.
Расчеты в пояснительной записке должны состоять из озаглавленных частей, соответствующих условию задач.
Расчет должен выполняться в следующей последовательности:
1. Записывается расчетная формула или уравнение в общем виде.
2. В формулы или уравнение, подставляются числовые значения, входящих в них величин и приводится результат вычисления. Промежуточные выкладки следует проводить только для сложных выражений.
Все задачи контрольных работ выполняются строго по шифру. Отклонения от шифра влечет за собой возврат контрольной работы и ее повторное выполнение в соответствии с шифром.
Выполненная контрольная работа передается для рецензирования преподавателю кафедры. Работа, выполненная с ошибками, возвращается студенту. Исправление ошибок производится на отдельных листах, вклеенных в не зачтенную работу, и отсылается на повторное рецензирование.
1. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ ИЛИ
СЖАТИЕ ПРЯМЫХ СТЕРЖНЕЙ
В первом разделе будут рассмотрены статически определимые стержни и стержневые системы, внутренние усилия или реакции связей которых можно определить с помощью уравнений статики.
Центральным растяжением (или центральным сжатием) называется такой вид деформации, при котором в поперечном сечении стержня возникает только одно усилие, продольная сила N (растягивающая или сжимающая). При центральном растяжении или сжатии внешние силы, включая опорные реакции, или их равнодействующие, направлены вдоль оси стержня.
Определение продольных сил
Метод сечений позволяет определять продольную силу в поперечном сечении любого силового участка. Стержень рассекают воображаемой плоскостью перпендикулярно его продольной оси, мысленно отбрасывают одну из образовавшихся частей, а действие на оставшуюся часть заменяют неизвестной продольной силой N (рис. 1,а). Далее составляют единственное уравнение равновесия оставшейся части å Z = 0.
Из этого уравнения определяют значение N, т.е. продольная сила в любом сечении бруса равна сумме проекций внешних сил, действующих на оставшуюся часть, на направление внешней нормали к сечению, взятой с обратным знаком.
Правило знаков
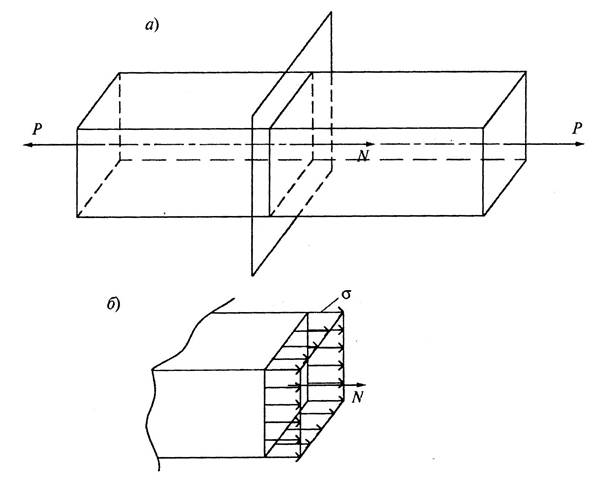 Силу N принято считать положительной при растяжении, т.е. когда она направлена от сечения. При сжатии, наоборот, продольная сила отрицательна и направлена к сечению.
Силу N принято считать положительной при растяжении, т.е. когда она направлена от сечения. При сжатии, наоборот, продольная сила отрицательна и направлена к сечению.
Эпюра (график) продольных сил дает наглядное представление о законе изменения этих сил на каждом силовом участке, стержня. Эпюра позволяет быстро находить опасные сечения стержня.
Силовой участок стержня – это участок, в котором продольная сила действует по одному определенному закону.
Границами силовых участков стержня являются места приложения внешних сил, включая и реакцию заделки стержня.
Напряжения
При центральном растяжении или сжатии в поперечных сечениях стержня возникают равномерно распределенные нормальные напряжения (рис. 1,б), равные отношению продольной силы N к площади поперечного сечения
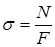 [Н/м2] = [Па] (1.1)
[Н/м2] = [Па] (1.1)
Эпюра напряжений для стержней постоянного сечения аналогична эпюре продольных сил, а при ступенчатом изменении площади сечения стержней, эпюра напряжений имеет скачки не только в местах приложения внешних сил, но и в местах изменения сечения. Это связано с тем, что напряжение обратно пропорционально площади сечения.
Границами участков при построении эпюры напряжений для стержня переменного сечения являются не только места приложения внешних сил, но и места ступенчатого изменения площади сечения.
Оценка прочности элементов конструкции, испытывающих растяжение или сжатие, производится по наибольшему нормальному напряжению.
Условие прочности, которое требуется для нормальной эксплуатации конструкции, записывается в виде:
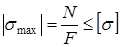 , (1.2)
, (1.2)
где 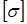 – допускаемое напряжение (задается в расчетных нормах или в справочниках).
– допускаемое напряжение (задается в расчетных нормах или в справочниках).
Допускаемые напряжения равны опасным напряжениям sоп, деленным на коэффициент запаса прочности n:
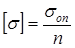 . (1.3)
. (1.3)
Для хрупких материалов за опасные напряжения принимают предел прочности sоп = sв, поэтому
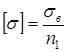 ,
,
для пластичных материалов – предел текучести sоп = sТ, следовательно,
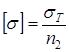 .
.
Очевидно, что коэффициент запаса n1, должен быть больше n2, так как после появления пластических деформаций стержень еще не разрушается.
Деформации и перемещения
Напряжения, не превосходящие предела пропорциональности, связаны с относительными деформациями законом Гука
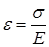 , (1.4)
, (1.4)
где 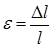 - относительная деформация;
- относительная деформация;
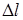 - абсолютная продольная деформация (удлинение или укорочение участка бруса длиной l с постоянными напряжениями в поперечных сечениях, м;
- абсолютная продольная деформация (удлинение или укорочение участка бруса длиной l с постоянными напряжениями в поперечных сечениях, м;
Е - модуль упругости при растяжении, Па.
Под действием продольных сил происходит удлинение или укорочение силовых участков стержня, а, следовательно, и всего стержня. Если на силовом участке продольная сила и площадь поперечного сечения постоянны, то
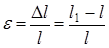 ,
,
где 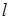 – длина стержня до деформации, м;
– длина стержня до деформации, м;
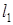 – то же, после деформации.
– то же, после деформации.
Подставляя выражения для 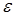 и
и 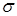 в (1.4), можно получить формулу для определения абсолютного удлинения стержня.
в (1.4), можно получить формулу для определения абсолютного удлинения стержня.
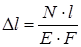 (1.5)
(1.5)
В случае, когда величина силы N изменяется в пределах силового участка по известному закону, деформация участка складывается из деформаций бесконечно-малых участков 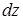 , по длине которых величину силы N можно считать постоянной. Тогда, применяя формулу (1.5) можно записать
, по длине которых величину силы N можно считать постоянной. Тогда, применяя формулу (1.5) можно записать
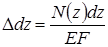 . (1.6)
. (1.6)
Полная деформация участка
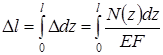 ; (1.7)
; (1.7)
Если на участке с постоянным поперечным сечением действует равномерно распределенная продольная погонная нагрузка t 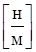 , то усилие
, то усилие 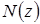 от этой нагрузки будет изменяться по закону
от этой нагрузки будет изменяться по закону
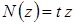 . (1.8)
. (1.8)
Подставляя (1.8) в (1.7), получим
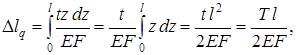 (1.9)
(1.9)
где 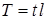 - равнодействующая равномерно распределенной погонной нагрузки на данном участке.
- равнодействующая равномерно распределенной погонной нагрузки на данном участке.
Для стержня, имеющего несколько силовых участков, абсолютное изменение длины стержня определяется как алгебраическая сумма деформаций отдельных силовых участков:
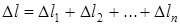 , (1.10)
, (1.10)
где 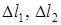 - абсолютные деформации соответствующих силовых участков стержня, определяемые по формуле (1.5) и (1.9).
- абсолютные деформации соответствующих силовых участков стержня, определяемые по формуле (1.5) и (1.9).
Перемещение поперечных сечений стержня вдоль его оси обозначается буквой U и является следствием деформации силовых участков стержня.
Перемещение произвольного сечения стержня равно абсолютному удлинению той части стержня, которая заключена между этим сечением и заделкой. Если известно перемещение 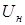 сечения в начале участка, длиной l, то перемещение
сечения в начале участка, длиной l, то перемещение 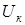 сечения в конце участка в котором действует нормальная сила
сечения в конце участка в котором действует нормальная сила 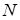 и, кроме того, по длине участка приложена равномерно распределенная нагрузка, может быть вычислено по формуле
и, кроме того, по длине участка приложена равномерно распределенная нагрузка, может быть вычислено по формуле
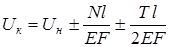 ; (1.11)
; (1.11)
Знаки у слагаемых определяются соответствием выбранного положительного направления 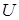 и направлением действия сил.
и направлением действия сил.
Отсюда следует, что перемещение поперечных сечений стержня может происходить и на участках, не подверженных деформации, а как результат влияния деформации соседних силовых участков. Это основное отличительное свойство перемещения от деформации.
Определяют перемещения по формуле (1.11) и начинают от неподвижного конца, т.е. от заделки.
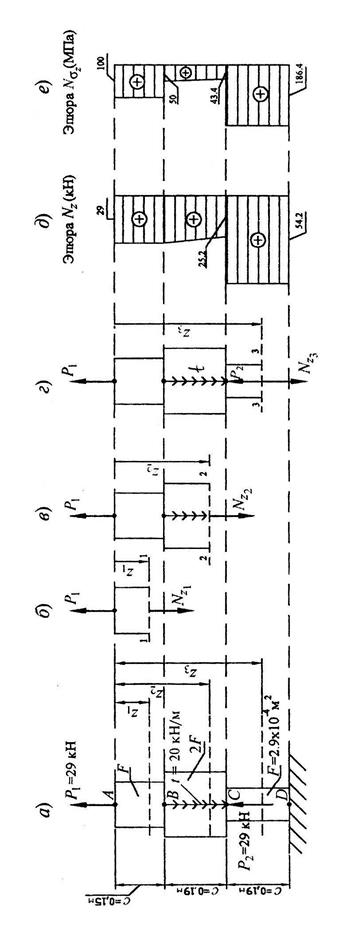
Пример 1. Стальной стержень (Е = 2×105 МПа), один конец которого жестко защемлен, другой – свободен, находится под действием продольных сил Р и распределенной нагрузки t = 20 кН/м. Продольные силы и нагрузка вызваны взаимодействием стержня с остальными частями механизма, не показанными на схеме. Отдельные участки стержня имеют различную площадь поперечного сечения, F или 2F (рис.2,а).
Требуется:
1) сделать схематический чертеж бруса по заданным размерам, соблюдая масштаб длин по вертикали;
2) вычислить значения продольной силы N и нормального напряжения s, построить их эпюры;
3) найти перемещение точки В.
Решение
Расчет на жесткость
Выражаем относительные углы закручивания через 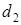 .
.
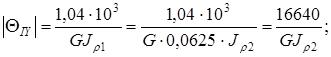
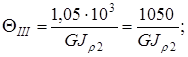
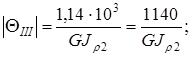
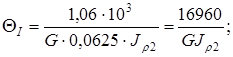
Следовательно, на первом участке имеет место максимальный угол закручивания.
По условию жесткости, переведя градусы в радианы, получим
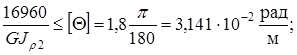
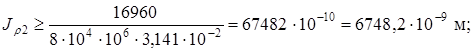
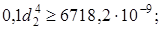
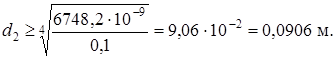
Из условий прочности и жесткости 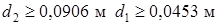 . Округляем до целых мм:
. Округляем до целых мм: 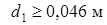 , отсюда
, отсюда 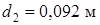
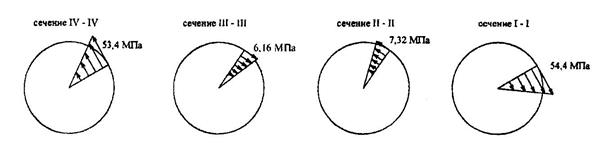
IV. Построение эпюр касательных напряжений t в поперечных
сечениях вала (рис.7)
Сечение I- I
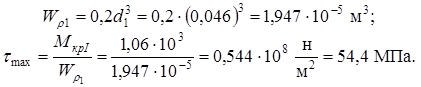
Сечение II-II
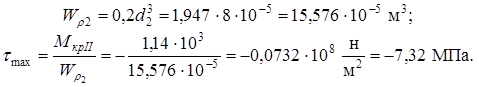
Сечение III-III
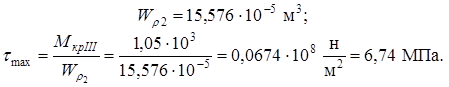
Сечение IY-IY
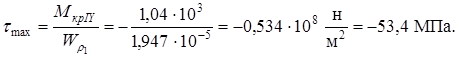
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

21/1/14 Одобрено кафедрой
«Сопротивление материалов
и строительная механика»
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Методические указания к выполнению
Контрольной работы № 1
для студентов III курса
Специальностей:
Локомотивы (Т)
Вагоны (В)
Дата: 2019-12-22, просмотров: 665.