Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В данной дипломном проектирование мною был проведен расчет и конструирование многопустотной панели перекрытия. 

Требуется рассчитать и сконструировать сборные железобетонные конструкции междуэтажного перекрытия гражданского здания при следующих данных: поперечный пролет l₁=6м, продольный шаг пролета l₂=3м, временная нагрузка на перекрытие pⁿ=1800Н/м². Несущими элементами перекрытия являются многопустотная панель с круглыми пустотами, имеющая номинальную длину 6м, ширину1,5м, высоту 22см.

 

 

Определение нагрузок и усилий.

На 1м длины панели шириной 150см действуют следующие нагрузки, Н/м.  таблица 5.

Таблица 5

Нагрузки на сборное междуэтажное перекрытие

Вид нагрузки	Нормативная нагрузка, Н/м²	Коэффициент надежности по нагрузке γf	Расчетная нагрузка, Н/м²
Постоянная: - от линолиумного пола t=0,004м, ρ=300кг/м³ - от шлакобетонного пола t=0,065м, ρ=1600кг/м³ - от керамзитобетонной панели t=0,06м, ρ=1300кг/м³ - от пенобетонной звукоизоляционной плиты t=0,06м, ρ=500кг/м³	12   1040     780     300	1,3   1,2     1,1 Окончание таблицы 5   1,2	15,6   1248     858     360
Итого:	gn=2132	-	g=2481,6
Временная: - кратковременная - длительная	1500 300	1,3 1,3	1950 390
Итого:	pn=1800	-	p=2340
Полная нагрузка: - постоянная и длительная - кратковременная	2432 1500	1,3 1,3	3161,6 1950
Итого:	gn+pn=3932	-	g+p=4821,6

 

- кратковременная нормативная: pⁿ=1500·1?5=2250

- кратковременная расчетная: p=1950·1,5=2925

- постоянная и длительная нормативная: qⁿ=2432·1,5=3648

- постоянная и длительная расчетная: q=3161·4742,4

- итого нормативная: qⁿ+ pⁿ=3648+2250=5898

- итого расчетная: q+ p=4742,4+2925=7667,4

Расчетный изгибающий момент от полной нагрузки γ_n=0,95:

M= ql₀²γ_n/8

L₀=6-0,2/2-0,1/2=6-0,1-0,05=5,85м

M=7667,4·5,85²·0,95/8=31159,71Н·м

Расчетный изгибающий момент от полной нормативной нагрузки (для расчета прогибов и трещиностойкости) при γ_f=1:

Mⁿ= qⁿ l₀²γ_n/8=5898·5,85²·0,11875=23969H·м

Аналогично, от нормативной постоянной и длительной временной нагрузки:

M_ld=3648·5,85²·0,95/8=14825Н·м

 

Нормативной кратковременной нагрузки:

M_cd=2250·34,2225·0,11875=9144Н·м

Максимальная поперечная сила на опоре от расчетной нагрузки:

Q= q l₀γ_n/2

Q=7667,4·5,85·0,95/2=21306Н

То же, от нормативной нагрузки:

Qⁿ=5898·5,85·0,475=16389H

Q_ld=3648·5,85·0,475=10137H

 

Подбор сечения.

Для изготовления сборной панели принимаем: бетон класса В30, E_b=32,5·10⁴МПа, R_b=17МПа, R_bt=1,2Мпа, γ_b2=0,9; продольную арматуру – из стали класса А-II, R_s=280МПа, поперечную арматуру – из стали класса А-I, R_s=225МПа и R_sw=175МПа; армирование – сварными сетками и каркасами; сварные сетки в верхней и нижней полках панели – из проволоки класса Вр-I, R_s=360МПа при d=5мм и R_s=365МПа при d=4мм.

Панель рассчитываем как балку прямоугольного сечения с заданными размерами b×h=150×22см (где b – нормативная ширина; h – высота панели). Проектируем панель шестипустотной.

В расчете поперечной сечение пустотной панели приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции.

 Вычисляем:

d=15,9 – диаметр пустот.

h₁=0,9d=0,9·15,9=14,3см

h_f=h’_f=(h-h₁)/2=(22-14,3)/2=3,85см≈3,8см

расчетная ширина сжатой полки b’_f=147cм;

b=147-7·14,3=61,2см

 

 

Расчет по прочности нормальных сечений.

Предварительно проверяем высоту сечения панели перекрытия из условия обеспечения прочности при соблюдении необходимой жесткости по формуле:

h=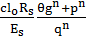

h=18·585·280/2,1·10⁵×2·2432+1500/3932=21,464см

qⁿ=gⁿ+pⁿ=3932Н/м²

Принятая высота сечения h=22см достаточна. Отношение h’_f/h=3,8/22,464=0,169>0,1; в расчете вводим всю ширину полки b’_f=147см.

A_o=M/R_bγ_b2b_fh_o²

h_o=h-a=19см

A_o­=3115971/17·0,9·147·19²·100=0,038

По таблице 2.12 учебника Мандрикова находим ξ=0,04

η=0,98; r_o=5,05

x=ξ·h_o=0,04·19=0,76см<h’_f=3,8 нейтральная ось проходит в пределах сжатой полки.

Площадь сечения продольной арматуры:

A_s= 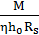 =3115971/0,98·19·280·100=5,98см²

Предварительно принимаем 7Ø12А-II

A­_s­=7,92см²

А также учитываем сетку С-I 1470·6000  (ГОСТ 8478-81),

A­_s1­=7·0,116=0,812см²

∑A_s=0,812+7,92=8,732 см²; стержни диаметром 12 мм распределяем по два в крайних ребрах и два в одном среднем ребре.

Расчет по прочность наклонных сечений.

Проверяем условие необходимости постановки поперечной арматуры для многопустотных панелей Q_max=21,3кН.

Вычисляем проекция с наклонного сечения по формуле: с=φ_b2(1+φ_f+φ_n)R_btbh²_o/Q_b=B_b/Q_b

φ_b2=2 – для тяжелого бетона.

φ_f=7·0,75 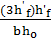 =7·0,75×3·3,8·3,8/61,2·19=0,196<0,5

φ_n=0

B_b= φ_b2(1+ φ_f+φ_n)R_btγ_b2bh²_o=2·(1+0,196)·1,2·0,9·61,2·19²·100=57·10⁵H·см

В расчетном наклонном сечении Q_b=Q_sw=Q/2,следовательно,

c=B_b/(0,5Q)=57·10⁵/(0,5·21300)=535см>2h_o=2·19=38см

Принимаем с=38см

Q_b=B_b/c=57·10⁵/38=1,5·10⁵H=150кН>Q=21,3кН. Следовательно, поперечная арматура по расчету не требуется.

Поперечную арматуру предусматриваем из конструктивных условий, располагая ее с шагом: s≤h/2=22/2=11см, s≤15см.

Назначаем поперечные стержни диаметром 6мм класса А-I через 10см у опор на участках длиной ¼ пролета. В среднем ½ части панели для связи продольных стержней каркаса по конструктивным соображениям ставим поперечные стержни через 0,5м. Если в нежную сетку С-1 включить рабочие продольные стержни, то приопорные каркасы можно оборвать в ¼ пролёта панели.

 

Определение прогиба.

Момент в середине пролета от полной нормативной нагрузки Mⁿ=23969H·м; от постоянной и длительной нагрузок M_ld=14825Н·м; от кратковременной нагрузки M_cd=9144H·м/

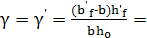(147-61,2)·3,8/61,2·19=0,28

μα= 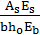 =8,012·2,1·10⁵/61,2·19·32500=0,04

λ_lim=23 при μα=0.07 и арматура класса А-II.

Общая оценка деформативности панели:

l/h_o+18h_o/l≤ λ_lim

l/h_o=585/19=30,79>10

l/h_o≤ λ_lim

l/h_o=30,79> λ_lim=23

условие не удовлетворяется, требуется расчет прогиба.

Прогиб в середине пролета панели по формуле от постоянных и длительных наагрузок.

F_max=Sl²/r_c= 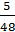6,25²1/r_c

 

 

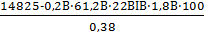=× =1.8·10^-5см^-1

f_max=(5/48)·585²·1,8·10^-5=0,64см, что меньше f_lim=3см.

 

Расчет панели по раскрытию трещин.

Панель перекрытия относится к третьей категории трещиностойкости как элемент, эксплуатируемый в закрытом помещении и армированный стержнями из стали класса A-II. Предельно допустимая ширина раскрытия трещин a_crc1=0,4мм и a_crc2=0,3мм.

Для элементов третьей категории трещиностойкости, рассчитываемых по раскрытию трещин, нормальных к продольной оси, при действии кратковременных и длительных нагрузок должно соблюдаться условие

a_crc=a_crc1-a_crc2+ a_crc3<a_crc,max.

a_crc1-a_crc2 – приращение ширины раскрытия трещин в результате кратковременного увеличения нагрузки от постоянной и длительной до полной;

a_crc3 – ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок.

Ширину раскрытия трещин определяем по формуле.

a_crc=δφ_lη 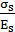20(3,5-100μ) 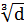δ_a

a_crc1=0,4мм

a_crc2=0,3мм

a_crc=a_crc1-a_crc2+a_crc3<a_crc,max.

δ=1

η=1

d=2,3

E_s=2,1·10⁵МПа для стали класса A-II

δ_a=1, т.к. а₂=3см<0,2/22=0,2/2,2=4,4см.

φ_l­=1 – при кратковременной нагрузки.

φ_l=1,6-15μ – при постоянной и длительной нагрузки.

μ= =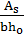

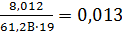
φ_l=1,6-15·0,013=1.4

σ_s=M/A_sz₁=M/W_s

z₁=h_o[1- ]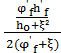

φ’_f=0,55

h’_f/h_o=3,8/22=0,172

h_o=19см

ξ=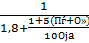

λ=φ’_f[1-h’_f/(2h­_o­­)]=0,55[1-3,8/(2·19)]=0,485

Значение δ от действия всех нормативных нагрузок:

δ=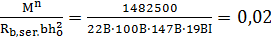

От действия постоянных и длительных нагрузок:

δ_ld=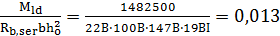

μα=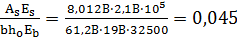

Вычисляем ξ при кратковременном действие всей нагрузки:

ξ==0,20

z₁=19[1-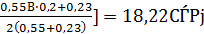

Упругопластический момент сопротивления железобетонного таврового сечения после образования трещин:

W_s=A_sx₁=8,012·18,22=145,98см³

Расчет по длительному раскрытию трещин.

M_ld=14,825кН·м

Напряжение в растянутой арматуре при действии постоянных и длительных нагрузок:

σ_s2=M_ld/W_s=14,825·10⁵/145,98=102МПа

Ширина раскрытия трещин от действия постоянной и длительной нагрузок при φ_l=1,4

A_crc3=1·1·1,4· 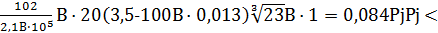a_crc,max=0,3м

Условие удовлетворяется.

Расчёт по кратковременному раскрытию трещин.

Mⁿ=23кН·м

M_ld=14кН·м

Напряжение в растянутой арматуре при совместном действие всех нормативных нагрузок: σ_s1=Mⁿ/W_s=23·10⁵/145,98=157,56МПа

Приращение напряжения от кратковременного увеличения нагрузки от длительно действующей до её полной величины Δσ_s=σ_s1-σ_s2=157,56-102=55,56МПа.

Соответствующее приращение ширины раскрытия трещин при φ_l=1:

Δa_crc=a_crc1-a_crc2=1·1·1·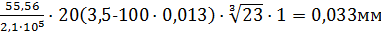

Ширина раскрытия трещин при совместном действии всех нагрузок: a_crc=0,033+0,084=0,117<a_crc,max.=0,4мм, т.е. условие удовлетворяется.

Значение a_crc можно подсчитывать без предварительного вычисления напряжений Δσ_s: W_s=145,48см³.

a_crc1=1·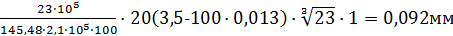

a_crc2=1·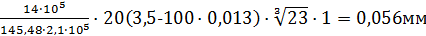

a_crc3=1·1·1,4· 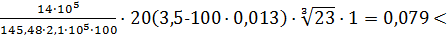a_crc2=0,3мм

a_crc=a_crc1-a_crc2+ a_crc3=0,092-0,056+0,079=0,115мм<a_crc,max.=0,4мм

 

Проверка по раскрытию трещин, наклонных к продольной оси.

Ширину раскрытия трещин, наклонных к продольной оси элемента и армированных поперечной арматурой, определяют по формуле из СНиПа 2.03.01-84:

a_crc=φ_l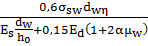

φ_l=1

η=1,4

d_w=7ØA-I – диаметр поперечных стержней (хомутов).

a=E_s/E_b=2,1·10⁵/3,25·10⁴=6,46

μ_w=A_sw/(bs)

A_sw=3Ø6A-I – площадь сечения поперечных стержней.

A_sw=3·0,283=0,85см²

μ_w=0,85/(61,2·10)=0,0014

Напряжение в поперечных стержнях (хомутов): σ_sw=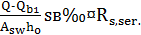

Q_b1=0,8φ_b4(1+φ_n)R_bt,ser.bh_o²/c

φ_n=0

γ_f=1

c=2h_o=2·19=38см

Q_bt=0,8·1,5·1·1,8·100·61,2·19²/38=125·10³H

σ_sw= 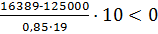 (получается отрицательная величина)

Так как σ_sw по расчету величина отрицательная, то раскрытие трещин, наклонных к продольной оси, не будет.

 

Проверка панели на монтажные нагрузки.

Панель имеет четыре монтажных петли из стали класса А-I, расположенные на расстояние 70см от концов панели. С учетом коэффициента динамичности k_d=1,4 расчетная нагрузка от собственного веса панели:

q=k_dγ_fgb=1,4·2,2·3080·1,5=14229,6H/см

q=h_redρ=0,11·28000=3080H/м²

Отрицательный изгибающий момент консольной части панели:

M=ql²/2=14229,6·0,7²/2=3486,252H·м

Этот момент воспринимается продольной монтажной арматурой каркасов.

Пологая, что z₁=0,9h_o, требуемая площадь указанной арматуры составляет:

A_s=M/z₁R_s=348625/0,9·19·280·100=0,73см²

Что значительно меньше принятой арматуры 3Ø10А-II, A_s=2,36см².

 При подъеме панели вес её может быть передан на две петли. Тогда усилие на одну петлю составляет: N=ql/2=14230·6/2=42690H

Площадь сечения арматуры петли: A_s=N/R_s=42690/210·100=2,03см²

Принимаем конструктивный стержень d=18мм и A_s=2,54см². [11]