Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

L = 34* 2 + 40*7 + 6*2 + 32*4 + 28*2+25 =569

Обозначим через

m(p₁, p₂,…, p_m, q₁, q₂,…, q_n)

вектор симплексных множителей или потенциалов. Тогда

Д_ij = m A_ij – c_ij          i = (1,…,m), j = (1,…,n)

 откуда следует

Д_ij = p_i + q_j– c_ij         i = (1,…,m), j = (1,…,n) (1)

Один из потенциалов можно выбрать произвольно, так как в системе одно уравнение линейно зависит от остальных. Положим, что р₁ = 0. Остальные потенциалы находим из условия, что для базисных клеток Д_ij = 0. В данном случае получаем

D₁₁ = 0,       p₁ + q₁ - c₁₁ = 0,     0+q₁ -2 = 0, q₁ = 2

D₁₂ = 0,       p₁ + q₂ - c₁₂ = 0,     0+q₂ -7 = 0, q₂ = 7

D₁₃ = 0,       p₁ + q₃ - c₁₃ = 0,     0+q₃ -2 = 0, q₃ = 2

D₂₃ = 0,       p₂ + q₃ – c₂₃ = 0,    p₂+2 -4 = 0, p₂ = 2

D₂₄ = 0,       p₂ + q₄ – c₂₄ = 0,    2+q₄ -2 = 0, q₄ = 0

D₃₄ = 0,       p₃ + q₄ – c₃₄ = 0,    p₃+ 0 -1 = 0, p₃ = 1

D₃₅ = 0,       p₃ + q₅ – c₃₅ = 0,    1+ q₅ -0 = 0, q₅ = -1

 

Затем по формуле (1) вычисляем оценки всех свободных клеток:

D₂₁ = p₂ + q₁ - c₂₁ = 2+2-1 = 3

D₃₁ = p₃ + q₁ - c₃₁ = 1+2 -3 = 0

D₂₂ = p₂ + q₂ – c₂₂ = 2+7-5 = 4

D₃₂ = p₃ + q₂ – c₃₂ = 1+7-4 = 4

D₃₃ = p₃ + q₃ – c₃₃ = 1+2-6 = 3

D₁₄ = p₁ + q₄ – c₁₃ = 0+0-3 = 3

D₁₅ = p₁ + q₅ – c₁₅ = 0+(-1) = -1

D₂₅ = p₂ + q₅ – c₂₅ = 2+(-1) = 1

 

Находим наибольшую положительную оценку max (D_ij > 0) = 4 = D₂₂

Для найденной свободной клетки 22 строим цикл пересчета - замкнутую ломаную линию, соседние звенья которой взаимно перпендикулярны, сами звенья параллельны строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке, а все остальные - в занятых клетках. Это будет 22-12-13-23. Производим перераспределение поставок вдоль цикла пересчета

40	6		40-r	6+r		8	38
	32		r	32-r		32	0

 

 

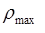= 32

 

Получаем второе базисное допустимое решение:

 

 

Потребление	b1 =34	b2 =40	b3 =38	b4 =53	b5 =5
Производство
а1 =80	2 34	7 8	2 38	3	0 *	p1 = 0
a2 =60	1	5 32	4	2 28	0	p2 = -2
a3 =30	3	4	6	1 25	0 5	p3 = -3
	q1 = 2	q2 = 7	q3 = 2	q4 = 4	q5 = 3

 

Находим новые потенциалы, новые оценки.

 

D₁₁ = 0,       p₁ + q₁ - c₁₁ = 0,     0+q₁ -2 = 0, q₁ = 2

D₁₂ = 0,       p₁ + q₂ - c₁₂ = 0,     0+q₂ -7 = 0, q₂ = 7

D₁₃ = 0,       p₁ + q₃ - c₁₃ = 0,     0+q₃ -2 = 0, q₃ = 2

D₂₂ = 0,       p₂ + q₂ – c₂₂ = 0,    p₂+7 -5 = 0, p₂ = -2

D₂₄ = 0,       p₂ + q₄ – c₂₄ = 0,    -2+q₄ -2 = 0, q₄ = 4

D₃₄ = 0,       p₃ + q₄ – c₃₄ = 0,    p₃+ 4 -1 = 0, p₃ = -3

D₃₅ = 0,       p₃ + q₅ – c₃₅ = 0,    -3+ q₅ -0 = 0, q₅ = 3

 

Вычислим оценки свободных клеток:

 

D₂₁ = p₂ + q₁ - c₂₁ = -2+2-1 = -1

D₃₁ = p₃ + q₁ - c₃₁ = -3+2 -3 = -4

D₃₂ = p₃ + q₂ – c₃₂ = -3+7-4 = 0

D₂₃ = p₂ + q₃ – c₂₃ = -2+2-4 = -4

D₃₃ = p₃ + q₃ – c₃₃ = -3+2-6 = -7

D₁₄ = p₁ + q₄ – c₁₃ = 0+4-3 = 1

D₁₅ = p₁ + q₅ – c₁₅ = 0+3 = 3

D₂₅ = p₂ + q₅ – c₂₅ = -2+3 = 1

 

Находим наибольшую положительную оценку max (D_ij > 0) = 3 = D₁₅

 

8			*		8-r			r		3			5
32		28			32+r		28-r			37		23
		25	5				25+r	5-r				30

 

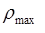= 5

Получаем третье базисное допустимое решение:

 

 

Потребление	b1 =34	b2 =40	b3 =38	b4 =53	b5 =5
Производство
а1 =80	2 34	7 3	2 38	3 *	0 5	p1 = 0
a2 =60	1	5 37	4	2 23	0	p2 = -2
a3 =30	3	4	6	1 30	0	p3 = -3
	q1 = 2	q2 = 7	q3 = 2	q4 = 4	q5 = 0

 

Находим новые потенциалы, новые оценки.

 

D₁₅ = 0,       p₁ + q₅ – c₁₅ = 0,    0+ q₅ -0 = 0, q₅ = 0

 

Вычислим оценки свободных клеток:

 

D₂₁ = p₂ + q₁ - c₂₁ = -2+2-1 = -1

D₃₁ = p₃ + q₁ - c₃₁ = -3+2 -3 = -4

D₃₂ = p₃ + q₂ – c₃₂ = -3+7-4 = 0

D₂₃ = p₂ + q₃ – c₂₃ = -2+2-4 = -4

D₃₃ = p₃ + q₃ – c₃₃ = -3+2-6 = -7

D₁₄ = p₁ + q₄ – c₁₄ = 0+4-3 = 1

D₂₅ = p₂ + q₅ – c₂₅ = -2+0-0 = -2

D₃₅ = p₃ + q₅ – c₁₅ = -3+0-0 = 0

 

 

Находим наибольшую положительную оценку max (D_ij > 0) = 1 = D₁₄

 

3		*		3-r		r				3
37		23		37+r		23-r		40		20

 

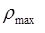= 3

 

Получаем третье базисное допустимое решение:

 

Потребление	b1 =34	b2 =40	b3 =38	b4 =53	b5 =5
Производство
а1 =80	2 34	7	2 38	3 3	0 5	p1 = 0
a2 =60	1	5 40	4	2 20	0	p2 = -1
a3 =30	3	4	6	1 30	0	p3 = -2
	q1 = 2	q2 = 6	q3 = 2	q4 = 3	q5 = 0

 

Находим новые потенциалы, новые оценки.

D₁₁ = 0,       p₁ + q₁ - c₁₁ = 0,     0+q₁ -2 = 0, q₁ = 2

D₁₃ = 0,       p₁ + q₃ - c₁₃ = 0,     0+q₃ -2 = 0, q₃ = 2

D₁₄ = 0,       p₁ + q₄ - c₁₄ = 0,     0+q₄ -3 = 0, q₄ = 3

D₂₄ = 0,       p₂ + q₄ – c₂₄ = 0,    p₂+3 -2 = 0, p₂ = -1

D₂₂ = 0,       p₂ + q₂ – c₂₂ = 0,    -1+q₂ -5 = 0, q₂ = 6

D₃₄ = 0,       p₃ + q₄ – c₃₄ = 0,    p₃+ 3 -1 = 0, p₃ = -2

D₁₅ = 0,       p₁ + q₅ – c₁₅ = 0,    0+ q₅ -0 = 0, q₅ = 0

 

Вычислим оценки свободных клеток:

 

D₂₁ = p₂ + q₁ - c₂₁ = -1+2-1 = 0

D₃₁ = p₃ + q₁ - c₃₁ = -2+2 -3 = -3

D₁₂ = p₁ + q₂ – c₁₂ = 0+6-7 = -1

D₃₂ = p₃ + q₂ – c₃₂ = -2+6-4 = 0

D₂₃ = p₂ + q₃ – c₂₃ = -1+2-4 = -3

D₃₃ = p₃ + q₃ – c₃₃ = -2+2-6 = -6

D₂₅ = p₂ + q₅ – c₂₅ = -1+0-0 = -1

D₃₅ = p₁ + q₅ – c₁₅ = -2+0-0 = -2

 

Все D_ij £ 0

 

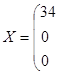
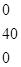
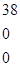
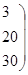
Общая стоимость всех перевозок для второго базисного допустимого решения:

L = 34*2 + 40*5 + 38*2 + 9 + 20*2+ 30 =423 – минимальная стоимость.

 

 

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕ КАПИТАЛЬНЫХ ВЛОЖЕНИЙ

Пусть производственное объединение состоит из четырех предприятий (n=4). Общая сумма капитальных вложений равна 700 тыс. рублей (b=700), выделяемые предприятиям суммы кратны 100 тыс. рублей. Значения функций fj(xj) приведены в таблице 1, где, например, число 50 означает, что если четвёртое предприятие получит 600 тыс. руб. капитальных вложений, то прирост прибыли на этом предприятии составит 50 тыс. руб.                                                                             

Таблица 1.

 

xj	0 100 200 300 400 500 600 700
f 1(xj)	0 20 33 42 48 53 56 58
f 2(xj)	0 22 37 49 59 68 76 82
f 3(xj)	0 10 29 42 52 60 65 69
f 4(xj)	0 16 27 37 44    48 50 56

Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x - x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение x’₂(x) . Заполняем таблицу 3.

Продолжая процесс, табулируем функции F3(x), x’₃(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x = 700.

Таблица 2

                     x - x2    0 100 200 300 400 500 600 700

                 F1(x - x2)      0 20 33 42 48 53 56 58

X2      f2(x2)     

0      0                         0 20 33 42 48 53 56 58

100  22                   22^* 42^* 55 64 70 75 78

200  37                   37 57^* 70^* 79  85 90

300  49                   49 69 82^* 91 97

400  59                   59 79 92^* 101^*

500  68                   68 88 101

600  76                   76 96

700  82                   82

                                                                                                                   

Таблица 3

xj	0 100 200 300 400 500 600 700
F2(x)	0 22 42 57 70 82 92 101
x’2(x)	0 100 100 200 200 300 400 400

Таблица 4

 

                      x - x3   0 100 200 300 400 500 600 700

                 F1(x - x3)      0 22 42 57 70 82 92 101

X3      f3(x3)     

0      0                         0 22^* 42^* 57^* 70 82 92 101

100  10                  10 32 52  67  80 92 102

200  29                  29 51     71^* 86^* 99^* 111

300  42                  42 64 84  99 112^*

400  52                  52 74 94 109

500  60                  60 82 102

600  65                  65 87

700  69                  69

Таблица 5

xj	0 100 200 300 400 500 600 700
F3(x)	0 22 42 57 71 86 99 112
x’3(x)	0 0  0  0 200 200 200 300

Таблица 6

 

                      x - x4   0 100 200 300 400 500 600 700

                 F1(x - x4)      0 22 42 57 71 86 99 112

X4      f4(x4)     

0      0                                                                                           112

100  16                                                                           115^*

200  27                                                                  113

300  37                                                        108

400  44                                              101

500  48                                    90

600  50                           77

700  56                  56

Наибольшее число на этой диагонали: Zmax = 115 тыс. руб.,

причем четвертому предприятию должно быть выделено x*₄ = x’₄ (700) = 100 тыс. руб.

На долю остальных трех предприятий остается 600 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено x*₃ = x’₃ (700- x*₄) = x’₃ (600) = 200 тыс. руб.

Продолжая обратный процесс, находим        x*₂ = x’₂ (700 - x*₄ - x*₃) = x’₂(300) = 200 тыс. руб.

На долю первого предприятия остается x*₁ = 700 - x*₄ - x*₃ - x*₃ = 200 тыс. руб.

Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:

x*₁ =200; x*₂ =200; x*₃ = 200; x*₄ = 100.