Предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли
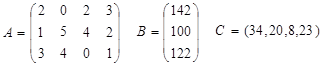 (1)
(1)
Требуется составить производственную программу (x1, x2, x3, x4), максимизирующую прибыль
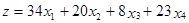 (2)
(2)
при ограничениях по ресурсам: 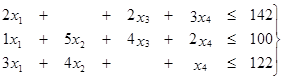 (3)
(3)
где по смыслу задачи 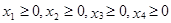 (4)
(4)
Получили задачу на условный экстремум. Для ее решения систему неравенств (3) при помощи дополнительных неотрицательных неизвестных х5, х6, х7 заменим системой линейных алгебраических
уравнений 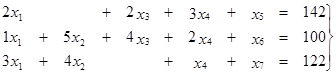 (5)
(5)
где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (5), удовлетворяющих условию неотрицательности х1³0, х2³0,… ,х5³0,…, х7³0. (6)
надо найти то решение, при котором функция (2) примет наибольшее значение.
Воспользуемся тем, что правые части всех уравнений системы (5) неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные х1, х2, х3, х4, получаем базисное неотрицательное решение
| |
первые четыре компоненты которого определяют производственную программу x1=0, x2=0, x3=0, x4=0 (8)
по которой мы пока ничего не производим. Из выражения (2) видно, что наиболее выгодно начинать производить продукцию первого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск в этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого придется записать для системы уравнений (5) общее решение
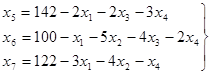 (9)
(9)
Мы пока сохраняем в общем решении х2=х3=х4=0 и увеличиваем только х1. При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств
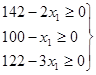 или
или 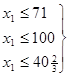 т.е. 0 £ х1 £
т.е. 0 £ х1 £ 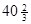
Дадим х1 наибольшее значение х1 = 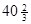 , которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (9). Получаем для системы уравнений (5) частное неотрицательное решение:
, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (9). Получаем для системы уравнений (5) частное неотрицательное решение:
х1= 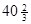 , х2=0, х3=0, х4=0; x5=
, х2=0, х3=0, х4=0; x5= 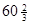 ; x6=
; x6= 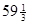 ; x7=0 (10)
; x7=0 (10)
Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (5), для получения которого достаточно было принять в системе (5) неизвестную х1 за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять третье, так как
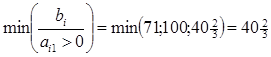 , а разрешающим элементом будет а31=3.
, а разрешающим элементом будет а31=3.
Остается заметить, что процесс решения обычно записывается в виде некоторой таблицы 1.
| ~ С | 34 20 8 23 0 0 0 | |||
| Базис | Н | x1 x2 x3 x4 x5 x6 x7 | Пояснения | |
| 0 | Х5 | 142 | 2 0 2 3 1 0 0 | z0 = 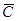 H H
|
| 0 | Х6 | 100 | 1 5 4 2 0 1 0 | 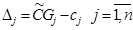
|
| 0 | Х7 | 122 | 3 4 0 1 0 0 1 | 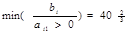
|
| z0 -z | 0 - z | -34 -20 -8 -50 0 0 0 | 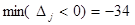
| |
| 0 | Х5 | 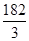
| 0 -8/3 2 7/3 1 0 -2/3 | min (26; 35,6;122)=26 |
| 0 | Х6 | 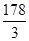
| 0 11/3 4 5/3 0 1 -1/3 | |
| 34 | Х1 | 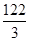
| 1 4/3 0 1/3 0 0 1/3 | |
| z0 -z | 4148/3-z | 0 76/3 -8 -35/3 0 0 34/3 | 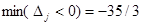
| |
| 23 | Х4 | 26 | 0 -8/7 6/7 1 3/7 0 -2/7 | |
| 0 | Х6 | 16 | 0 39/7 18/7 0 -5/7 1 1/7 | |
| 34 | Х1 | 32 | 1 12/7 -2/7 0 -1/7 0 3/7 | |
| z0 -z | 1686-z | 0 12 2 0 5 0 8 | все Dj ³0 |
Используя формулы исключения получаем для системы уравнений (5) новый предпочитаемый эквивалент и новую вспомогательную систему:
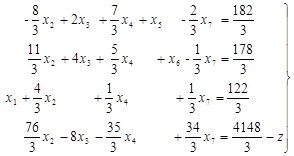 (11)
(11)
Первые три уравнения этой системы представляют некоторый предпочитаемый эквивалент системы уравнений (5) и определяют базисное неотрицательное решение (10) и производственную программу х1= 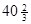 , х2=0, х3=0, х4=0, а из последнего уравнения системы (11) получается выражение функции цели через свободные переменные:
, х2=0, х3=0, х4=0, а из последнего уравнения системы (11) получается выражение функции цели через свободные переменные:
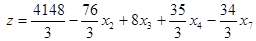
Очевидно, если имеется хотя бы один отрицательный коэффициент Dj при какой-нибудь переменной xj в последнем уравнении системы (11), то производственная программа не является наилучшей и можно далее продолжать процесс ее улучшения. Мы нашли в последнем уравнении системы (11) наименьший отрицательный коэффициент min(Dj<0) = - 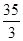 = D4. Поэтому принимаем х4 в системе (11) за разрешающую неизвестную, находим разрешающее уравнение по
= D4. Поэтому принимаем х4 в системе (11) за разрешающую неизвестную, находим разрешающее уравнение по 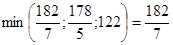 (12)
(12)
и исключаем х4 из всех уравнений системы (11), кроме первого уравнения. Укажем разрешающий элемент а14= 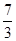 .
.
Преобразуем вспомогательную систему (11), по формулам исключения.
та система преобразуется к виду
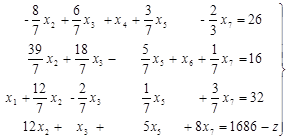 (13)
(13)
Первые три уравнения системы (13) представляют некоторый предпочитаемый эквивалент системы уравнений (5) и определяют базисное неотрицательное решение системы условий рассматриваемой задачи
x1=32, x2=0, x3=0, x4=26, x5=0, x6=16, x7=0 (14)
т.е. определяют производственную программу x1=32, x2=0, x3=0, x4=26 (15)
и остатки ресурсов:
первого вида х5=0
второго вида х6=16 (16)
третьего вида х7=0
Последнее уравнение системы (13) мы получаем, исключая х4. В последнем уравнении системы (13) среди коэффициентов при неизвестных в левой части уравнения нет ни одного отрицательного. Если из этого уравнения выразить функцию цели z через остальные неотрицательные переменные
z = 1686 - 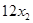 - 2x3 - 5x5 - 8 x7 (17)
- 2x3 - 5x5 - 8 x7 (17)
то становится совершенно очевидным (в силу того, что все xj³0), что прибыль будет наибольшей тогда, когда
x2=0, x3=0, x5=0, x7=0 (18)
Это означает, что производственная программа (15) является наилучшей и обеспечивает предприятию наибольшую прибыль zmax = 1686 (19)
Проверим соотношение H=Q-1B
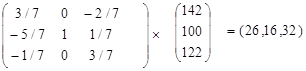
Итак, организовав направленный перебор базисных неотрицательных решений системы условий задачи, мы пришли к оптимальной производственной программе и указали остатки ресурсов, а также максимальную прибыль.
Следует обратить внимание на экономический смысл элементов последней строки последней симплексной таблицы. Например, коэффициент D2=12 при переменной х2 показывает, что если произвести одну единицу продукции третьего вида (она не входит в оптимальную производственную программу), то прибыль уменьшится на 12 единиц.
Воспользуемся тем, что в оптимальной производственной программе x2=0, x3=0. Предположим, что четвертую и третью продукции мы не намеревались выпускать с самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранив их нумерацию. Математическая модель задачи будет выглядеть следующим образом:
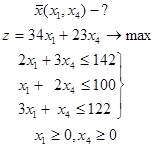


 |

ДВОЙСТВЕННАЯ ЗАДАЧА
Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.
Теперь представим себе, что знакомый предприниматель П, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у1 рублей за каждую единицу первого ресурса, у2 руб. – второго, у3 руб. – третьего. Возникает вопрос: при каких ценах у1, у2, у3 мы можем согласиться с предложением П.
 Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имели вид 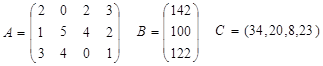
Для производства единицы продукции первого вида мы должны затратить, как видно из матрицы А, 2 единицы ресурса первого вида, 1 единицу ресурса второго вида и 3 единицы третьего (элементы первого столбца матрицы). В ценах у1, у2, у3 наши затраты составят 2у1 + 1у2 + 3у3, т.е. столько заплатит предприниматель П за все ресурсы, идущие на производство единицы продукции первого вида. На рынке за единицу первой продукции мы получили бы прибыль 34 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше 2у1 + 1у2 + 3у3 ³ 34.
Аналогично, для трех оставшихся видов продукции:
+ 5у2 + 4у3³20
2у1 + 4у2 ³8
3у1 + 2у2 + 1у3³23
Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 142у1 + 100у2 + 122у3 рублей. При поставленных нами условиях предприниматель П будет искать такие значения величин у1, у2, у3, чтобы эта сумма была как можно меньше. Подчеркнем, что здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.
Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у1, y2, y3) минимизирующий общую оценку всех ресурсов f = 142у1 + 100у2 + 122у3 (1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
2у1 + 1у2 + 3у3 ³ 34
+ 5у2 + 4у3³ 20 (2)
2у1 + 4у2 ³ 8
3у1 + 2у2 + 1у3³ 23
причем оценки ресурсов не могут быть отрицательными y1 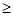 0, y2
0, y2 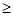 0, y3
0, y3 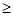 0. (3)
0. (3)
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений 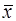 (х1, х2, х3, х4) и
(х1, х2, х3, х4) и 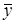 (y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
(y1, y2, y3) пары двойственных задач необходимо и достаточно выполнение условий
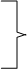 | |||
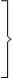 | |||
x 1 (2у1 + у2 + 3у3 - 34) = 0 y1 (2x1 + 2x3 + 3x4 - 142) = 0
x 2 ( 5у2 + 4у3- 20) = 0 y2 ( x1 +5x2 + 4x3 + 2x4 - 100) = 0
x 3 (2у1 + 4у2 - 8) = 0 y3 (3x1 +4x2 + x4- 122) = 0 .
x 4 (3у1 + 2у2 + у3 - 23) = 0
Ранее было найдено, что в решении исходной задачи х1>0, x4>0. Поэтому
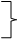 |
2y1 + y2 + 3y3 - 34 = 0
3y1 + 2y2 + y3 - 23 = 0
Если же учесть, что второй ресурс был избыточным и, согласно той же теореме двойственности, ее двойственная оценка равна нулю у2=0,
 то приходим к системе уравнений
то приходим к системе уравнений
2y1 + 3y3 - 34 = 0
3y1 + y3 - 23 = 0
откуда следует у1=5, у3=8.
Таким образом, получили двойственные оценки ресурсов у1=5; у2=0; у3=8, (4)
причем общая оценка всех ресурсов равна 1686.
Заметим, что решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка третьего ресурса у3=8 показывает, что добавление одной единицы третьего ресурса обеспечит прирост прибыли в 8 единицы.
ЗАДАЧА О "РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА"
При выполнении оптимальной производственной программы первый и третий ресурсы используются полностью, т.е. образуют ² узкие места производства ² . Будем их заказывать дополнительно. Пусть T(t1,t2,t3)- вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться услови
H + Q-1T 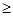 0.
0.
Задача состоит в том, чтобы найти вектор T (t1, 0, t3), максимизирующий суммарный прирост прибыли W = 5t1 + 8t3 (1) при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)
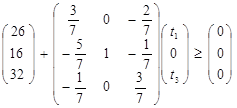 (2)
(2)
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида 
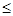
 (3)
(3)
причем по смыслу задачи t1 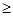 0, t3
0, t3 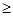 0. (4)
0. (4)
Переписав неравенства (2) и (3) в виде:
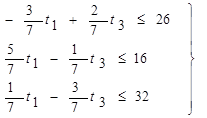 (5)
(5)
из условия (3) следует t1£142/3, t3£122/3 (6)
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
Эту задачу легко решить графически: см. рис. 2.
I.) -3/7t1+2/7t3= 26
II.) 5/7t1-1/7t3= 16
III.) 1/7t1-3/7t3 = 32
 M (458/15, 122/3)
M (458/15, 122/3)
Программа ²расшивки² имеет вид
t1=458/15, t2=0, t3=122/3 и прирост прибыли составит 5*458/15+8*122/3=478.
Сводка результатов приведена в таблице:
| Cj | 34 8 20 33 | b | x4+i | yi | ti |
| aij | 2 0 2 3 1 5 4 2 3 4 0 1 | 142 100 122 | 0 16 0 | 5 0 8 | 488/15 0 122/3 |
| Xj | 32 0 0 26 | 1686 | 478 | ||
| Dj | 0 12 2 0 |
Дата: 2019-12-22, просмотров: 356.