Устойчивость стенки балки должна быть обеспечена при любом напряжённом состоянии, т.е. условная гибкость стенки:

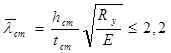
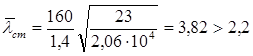 – условие не выполняется, следовательно, стенку балки необходимо укреплять парными поперечными рёбрами жёсткости.

Рёбра ставятся на равных расстояниях по длине всей балки. Расстояние между рёбрами не должно превышать amax=2*hcт=2*160=320 см, т.к. λст>3,2.

 В стенке, укреплённой только поперечными рёбрами, ширина каждого из парных симметричных рёбер жёсткости должна быть не менее:

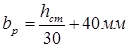и не менее 90мм,

bp=1600/30+40=93 мм, по [4 прил.2] принимаем bp=100 мм.

Толщина рёбра должна быть не менее

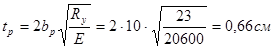
По [4 прил.2] принимаем tp=7 мм.

Проверка устойчивости стенки балки расчетом не требуется, если при наличии местных напряжений 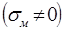 соблюдается неравенство:

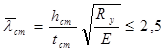
т.к. неравенство не соблюдается, то проверка устойчивости стенки балки должна производиться с учетом всех компонентов напряженного состояния.

Устойчивость стенки балки несимметричного сечения проверяется по формуле:

,

где   γст =0,9 – коэффициент для подкрановых балок

σ, τ, σм – нормальные, касательные, местные напряжения в рассчитываемом отсеке стенки от внешней нагрузки;

σкр, τкр, σкр – критические напряжения для отсека стенки.

Краевое сжимающее напряжение σ у расчетной границы отсека:

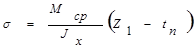
где  z₁=hcт/2+tn-z=80+1,6-5,491=76,12 см

М_ср, Q_ср – средние значения изгибающего момента и перерезывающей силы в пределах отсека.

Т.к. длина отсека a превосходит высоту h_ст, то σ и τ вычисляются по средним значениям момента М_ср и перерезывающей силы Q_ср для наиболее напряженного участка отсека длиной, равной расчетной высоте отсека h_ст.

Средний изгибающий момент отсека:

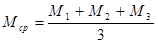
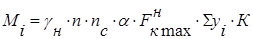
где α=1,05 – коэффициент, учитывающий собственный вес подкрановой балки, принимаемый по [4, табл. 2.1]

Σyi –  сумма ординат линии влияния

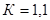 – коэффициент динамичности [3 п.4.9],

M1=0,95*1,1*0,85*1,05*540*(5,245+6,755)*4,4/12*1,1=243800 кНсм

M2=0,95*1,1*0,85*1,05*540*(5,245+6,755)*5,244/12*1,1=290500431970 кНсм

M3=0,95*1,1*0,85*1,05*504*2*5,245/21,1=290600 кНсм

Мср=(243800+290500+290600)/3=275000 кНсм

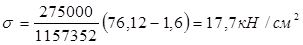
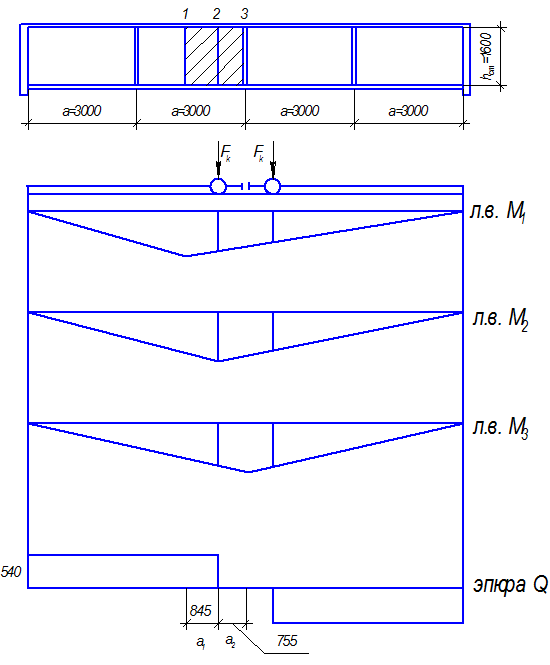
Среднее значение перерезывающей силы в пределах рассчитываемого отсека определяется по эпюре перерезывающих сил (см. рис.) по формуле:

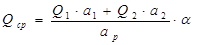
где  Q₁ – перерезывающая сила в пределах отсека, вычисленная только от действия подвижной крановой нагрузки F_к;

а_i – участок эпюры с постоянными ординатами в пределах отсека;

а_р=160 cм – расчетная ширина отсека стенки или участие отсека, равного h_ст.

Qcp=(540*84,5+0*75,5)*1,04/160=297 кН

Местные напряжения σм определены в пункте 5: σм=12,56 кН/см²

Касательные напряжения:

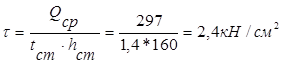
При отношении размеров отсека 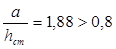 потеря устойчивости стенки балки асимметричного сечения может произойти как по одной, так и по двум полуволнам, поэтому проверка производится дважды:

I случай. Предполагая, что потеря устойчивости стенки происходит по одной полуволне, нормальные критические напряжения находятся по формуле:

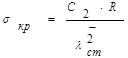
где  С₂ = 37,825 – коэффициент, принимаемый по [4 табл.2.4]

hb – расстояние от нейтральной оси до верхней границы отсека

hb=Z1-tn=76,12-1,6=74,52 см

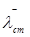 – условная гибкость стенки балки асимметричного сечения:

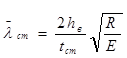
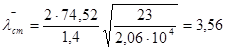
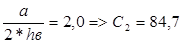
σкр=84,7*23/3,56²=153,7 кН/см²

Касательные критические напряжения:

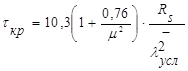
где  R_s=13,26 кН/см²

μ=1,875 – отношение большей сторон отсека a=300 cм к меньшей d=h_ст=160 см

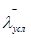– условная гибкость стенки по размеру d

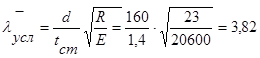
τкр=10,3*(1+0,76/1,875²)*13,26/3,82²=11,38 кН/см²

Критические местные напряжения:

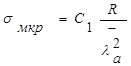
где  С₁ – коэффициент, принимаемый для сварных балок по [4, табл.2.3] в зависимости от степени упругого защемления стенки в поясах δ

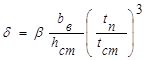
где  β – коэффициент, зависящий от условий работы сжатого пояса. При крановых рельсах, прикрепленных к поясу болтам, β=2.

δ=2*40*(1,6/1,4)³/160=0,75

Принимаем С₁ = 41,8

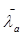– условная гибкость стенки по размеру а:

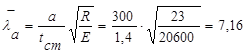
σмкр=41,8*23/7,16²=18,75 кН/см²

II случай. Предполагая, что потеря устойчивости стенки балки происходит по двум полуволнам, местные критические напряжения определяем по формуле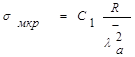

с подстановкой а/2 вместо а в [4, табл.2.3] и формулу :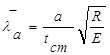

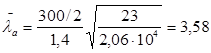
Принимаем С₁ = 17

σмкр=17*23/3,58²=30,51 кН/см²

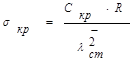
где  С₂ = 30 – коэффициент, принимаемый по [4 табл.2.4]

hb – расстояние от нейтральной оси до верхней границы отсека

hb=Z1-tn=76,12-1,6=74,52 см

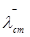 – условная гибкость стенки балки асимметричного сечения:

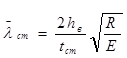
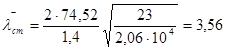
σкр=30*23/3,56²=54,44 кН/см²

Устойчивость стенки для полной длины волны:

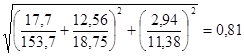0,81<0,9 – условие выполняется.

Устойчивость стенки для полуволны:

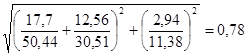, 0,78<0,9 –условие выполняется