Индивид принимает решения в долг периоде.

Величину дохода он определяеи сам, распределяя время (Т) на свободное (F) и рабочее (N). Размер дохода =w*N.

2 периода.

 Предпочтение индивида относительно потребления и свободного времени опр как 

U= (C0- a)^a(C1-a)^a(F0-b)^y

Потребление во 2ом периоде задано как C1 = (1 + i)(w(T0 – F0) – C0). При заданном доходе объемы C=C(i)- ; S=S(i)+

Увеличение дохода в любом из двух периодов сдвигает линию бюджетного ограничения вправо. Если потребление в первый период и потребление во второй период являются нормальными благами, то рост дохода, независимо от того, в какой период он происходит, увеличивает потребление в обоих периодах.

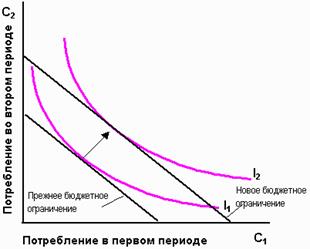
Комментарий: Если потребитель желает получить больше какого-либо блага по мере роста своего дохода, такое благо называется нормальным.

Таким образом, потребление зависит от текущей стоимости дохода в данном периоде и дисконтированной стоимости будущего дохода. Текущая стоимость дохода исчисляется как Y₁+[Y₂/(1+r)].

Модель Фишера утверждает, что потребление определяется тем, сколько потребитель ожидает получать доходов в течение всей своей жизни.

Предположения:

1. потребитель живет только в двух временных периодах;

2. к концу второго периода потребитель тратит весь накопленный доход

3. потребитель знает заранее размер своего дохода как в первом пе­риоде ( Y ₁ ), так и во втором ( Y ₂ );

4. потребитель может занимать средства или делать сбережения, то есть потребление в каждом периоде может быть как больше, так и меньше текущего дохода;

5. все переменные рассматриваются в реальном выражении;

6. потребление в обоих периодах является нормальным благом;

7. процентная ставка по займам совпадает с процентной ставкой по сбережениям и является const .

Обозначим потребление в первом периоде С₁, а во втором - C₂ , ре­альную ставку процента г. В первом периоде индивид потребляет C₁ и сберегает (Y₁-С₁).

Во втором периоде индивид потребляет С₂ и сбережения первого периода, увеличенные с учетом процента на сбережения: C₂= Y₂+(Y₁-С₁)(1+r).

Сбережения(Y₁-С₁)<0, если потребитель в первом периоде по­требляет больше текущего дохода, занимая под свой доход второго периода.

Необходимо решить задачу U(C1C2)—max при условии межвременного бюджетного ограничения C₁+C₂/(1+r)=Y₁+Y₂/(1+r) U-ф-ция полезности

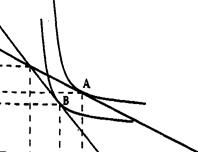
А – оптимум – т. касания кривой безразличия и линии бюджетного ограничения

В т. А MRS потребления первого пе­риода потреблением во втором периоде равна отношению цен рассматриваемых благ или тангенсу угла наклона бюджетного ограни­чения: MRS = 1+г.

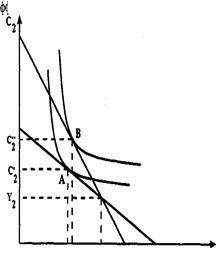Увеличение дохода в любом периоде увеличивает дисконтированный суммарный доход и на графике сдвигает линию б.о. параллельно вправо. Потребление в 1 периоде возрастает даже при текущем неизменном доходе, если в будущем ожидается увеличение дохода.

Увеличение r означает, что линия б.о. становится круче, т. к. меняется соотношение цен потребле­ния в 1 и 2 период. Потребитель может теперь больше, чем раньше, потребить в будущем, отказываясь от единицы потребления в настоящем.

В модели рассматриваются потребители 2х типов: сберегатели и заемщики

При росте r сберегатель получает больший доход на сбережения первого периода, поэтому его доход во втором периоде возрастает и он сможет потребить больше, чем раньше, в обоих периодах (эффект дохода). Таким образом, сберегатель будет потреблять во 2 периоде больше, чем раньше. Потребление 1 периода может как увеличиться (эффект дохода окажет большее влияние, чем эффект замещения), так и уменьшиться (эффект замещения перекроет эффект дохода).

Для "заемщика" увеличение ставки процента уменьшит потребление в первом периоде и может как увеличить, так и уменьшить потребление во 2периоде.

Если "заемщик" встречается с ограничением по заимствованию (не может получить кредит для увеличения своего текущего потребления), то он вынужден будет ограничить размеры потребления первого и второго периодов величиной текущего дохода соответствующего периода