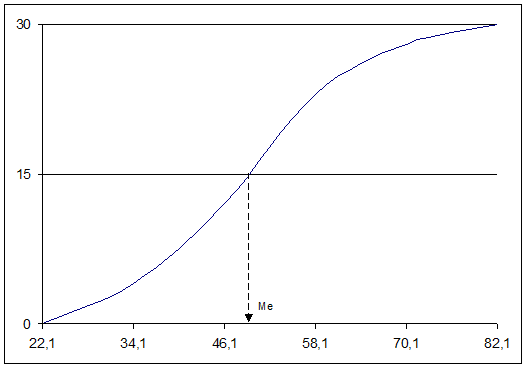
Ме ≈ 49 тыс.руб.
Вывод. 50% домохозяйств имеют валовой доход в среднем на одного члена домохозяйства менее 49 тыс.руб., а 50% более 49 тыс.руб.
3. Рассчитаем характеристики ряда распределения:
Среднее арифметическое:
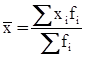
Таблица 2.4
Расчет характеристик ряда распределения
| xi | fi | xi . fi | xi - 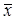
| (xi - 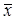 )2 )2
| (xi - 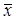 )2 fi )2 fi
|
| 28,1 | 4 | 112,4 | -21,2 | 449,44 | 1797,8 |
| 40,1 | 8 | 320,8 | -9,2 | 84,64 | 677,12 |
| 52,1 | 11 | 573,1 | 2,8 | 7,84 | 86,24 |
| 64,1 | 5 | 320,5 | 14,8 | 219,04 | 1095,2 |
| 76,1 | 2 | 152,2 | 26,8 | 718,24 | 1436,5 |
| ∑ | 30 | 1479 | 14 | 1479,2 | 5092,8 |
| Среднее | 49,3 | 169,76 |
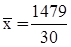 = 49,3 тыс.руб.
= 49,3 тыс.руб.
Среднеквадратическое отклонение:
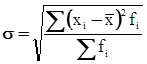
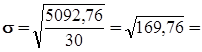 13,029 тыс.руб.
13,029 тыс.руб.
Коэффициент вариации
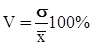
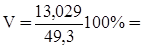 26,4%
26,4%
Так как V=26,4<33%, то можно сделать вывод, что совокупность однородная, средняя величина является типичной характеристикой.
4. Вычислим среднюю величину по исходным данным

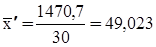
Сравним 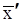 и
и 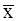
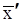 ≠
≠ 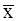
Значения 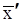 и
и 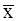 не совпадают, это объясняется тем, что при группировке возникают ошибки. Для большей точности следует увеличить число интервалов.
не совпадают, это объясняется тем, что при группировке возникают ошибки. Для большей точности следует увеличить число интервалов.
Выводы:
По полученной группировке можно сделать вывод, что наибольшее число домохозяйств (11 из 30) имеют валовой доход от 46,1 до 58,1 тыс.руб.
Наиболее часто встречающееся значение (мода) валового дохода в среднем на одного члена домохозяйства составляет 49 тыс.руб.
Медиана (значение признака у средней единицы ранжированного ряда) равна 49 тыс.руб., т.е. 50% домохозяйств имеют валовой доход в среднем на одного члена домохозяйства менее 49 тыс.руб., а 50% более 49 тыс.руб.
Среднее арифметическое равно 49,3 тыс.руб.
Среднеквадратическое отклонение составляет 13,029 тыс.руб.
Коэффициент вариации 26,4% показывает процентное отношение Среднего квадратического отклонения к средней арифметической. Вариация незначительная, т.е. домашние хозяйства однородны по валовому доходу на одного члена домохозяйства.
Задание 2
Связь между признаками – валовой доход и расходы на продукты питания в среднем на одного члена домохозяйства.
а) Метод аналитической группировки
Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Сопоставляя затем изменения результативного признака по мере изменения факторного можно выявить направление, характер и тесноту связи между ними.
Сгруппированные данные по величине валового дохода представлены в таблице 2.5:
Таблица 2.5
Рабочая аналитическая таблица
| № групп | Групп. Домохозяйств | № домохозяйства п/п | Валовой доход | Расходы на продукты питания | Кол-во домохозяйств в группе |
| I | 22,1 - 34,1 | 3 | 22,1 | 10,2 | 4 |
| 4 | 26,3 | 12,4 | |||
| 30 | 26,5 | 11,6 | |||
| 21 | 29,9 | 13,4 | |||
| Итого по группе | 104,8 | 47,6 | |||
| II | 34,1 - 46,1 | 25 | 34,5 | 14,8 | 8 |
| 1 | 35,8 | 14,9 | |||
| 19 | 37,9 | 17,7 | |||
| 5 | 39 | 16,1 | |||
| 6 | 40 | 16,6 | |||
| 13 | 41 | 17,1 | |||
| 8 | 42 | 17,4 | |||
| 26 | 45 | 18 | |||
| Итого по группе | 315,2 | 132,6 | |||
| III | 46,1 - 58,1 | 7 | 46,2 | 18,4 | 11 |
| 15 | 46,7 | 18,6 | |||
| 29 | 46,8 | 18,4 | |||
| 24 | 48 | 18,6 | |||
| 20 | 48,3 | 19,3 | |||
| 28 | 48,6 | 17,8 | |||
| 23 | 50,6 | 20,3 | |||
| 16 | 53,8 | 20,5 | |||
| 18 | 54,5 | 19,9 | |||
| 22 | 56 | 20 | |||
| 14 | 57 | 20,5 | |||
| Итого по группе | 556,5 | 212,3 | |||
| IV | 58,1 - 70,1 | 27 | 58,4 | 21 | 5 |
| 2 | 65,1 | 22,2 | |||
| 12 | 67 | 23 | |||
| 17 | 67,8 | 23,2 | |||
| 11 | 68,8 | 22,2 | |||
| Итого по группе | 327,1 | 111,6 | |||
| V | 70,1-82,1 | 10 | 75 | 24,3 | 2 |
| 9 | 82,1 | 25,2 | |||
| Итого по группе | 157,1 | 49,5 | |||
| Всего | 1470,7 | 553,6 | 30 |
В каждой выделенной группе определяем суммарную величину расходов на продукты питания по совокупности домохозяйств в группе и в расчете на одно домохозяйство.
Таблица 2.6
Аналитическая группировка домохозяйств по размеру валового дохода
Дата: 2019-12-22, просмотров: 317.