Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В статистике потребления используются различные коэффициенты и индексы.

Динамика общего потребления изучается с помощью агрегатного индекса объема потребления I_оп, который рассчитывается следующим образом:

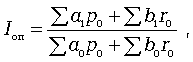                                         (7)

где a₁, a₀ - количество потребленных товаров в отчетном и базисном периодах; b₁, b₀ - количество потребленных услуг в отчетном и базисном периодах; p₀, r₀ - цена товара и тариф за определенную услугу в базисном периоде.

При статистическом исследовании зависимости объема потребления от дохода используется коэффициент эластичности К_э, который характеризует величину возрастания или снижения потребления товаров и услуг при росте дохода на 1% (в теории статистики это формула А. Маршалла):

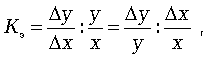                                      (8)

где х, у - начальные доход и потребление; 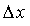, 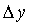- приращения начальных дохода и потребления за определенный период.

Если К_э > 1, то потребление растет быстрее, чем доходы.

Если К_э = 1, то между доходом и потреблением имеет место пропорциональная зависимость.

Если К_э < 1, то доход растет быстрее, чем потребление.[5]

 

Расчетная часть

 

Имеются следующие данные по домашним хозяйствам населения района (выборка 1%-ная механическая), тыс. руб.:

№ домохозяйства п/п

В среднем на одного члена домохозяйства

№ домохозяйства п/п

В среднем на одного члена домохозяйства

Валовой доход Расходы на продукты питания

Валовой доход

Расходы на продукты питания

1 35,8 14,9 16 53,8 20,5 2 65,1 22,2 17 67,8 23,2 3 22,1 10,2 18 54,5 19,9 4 26,3 12,4 19 37,9 17,7 5 39 16,1 20 48,3 19,3 6 40 16,6 21 29,9 13,4 7 46,2 18,4 22 56 20 8 42 17,4 23 50,6 20,3 9 82,1 25,2 24 48 18,6 10 75 24,3 25 34,5 14,8 11 68,8 22,2 26 45 18 12 67 23 27 58,4 21 13 41 17,1 28 48,6 17,8 14 57 20,5 29 46,8 18,4 15 46,7 18,6 30 26,5 11,6

Задание 1

По исходным данным:

1. Постройте статистический ряд распределения организа­ций по признаку валовой доход в среднем на одного члена домохозяйства, образовав пять группы с равными интервалами.

2. Постройте графики полученного ряда распределения. Графически определите значения моды и медианы.

3. Рассчитайте характеристики ряда распределения: сред­нюю арифметическую, среднее квадратическое отклоне­ние, коэффициент вариации.

4. Вычислите среднюю арифметическую по исходным дан­ным, сравните ее с аналогичным показателем, рассчитанным в п. 3 настоящего задания. Объясните при­чину их расхождения.

Сделайте выводы но результатам выполнения задания.

 

Решение

Обозначим: x - валовой доход в среднем на одного члена домохозяйства, тыс.руб.

n = 30, k = 5.

Найдем наименьшее и наибольшее значения

х_min = 22,1 тыс.руб.

х_max = 82,1 тыс.руб.

 

Определим размах выборки

R = х_max – х_min = 82,1 – 22,1 = 60 тыс.руб.

 

Ширина интервала

h = R/k = 60/5 = 12 тыс.руб.

Получаем следующие интервалы:

22,1 - 34,1; 34,1 - 46,1; 46,1 - 58,1; 58,1 - 70,1; 70,1-82,1

Таблица 2.2.

Рабочая группировочная таблица

№ групп	Групп. домохозяйств по валовому доходу в среднем на одного члена домохозяйства, тыс.руб.	№ домохозяйства п/п	Валовой доход	Расходы на продукты питания	Кол-во домохозяйств в группе
I	22,1-34,1	3	22,1	10,2	4
		4	26,3	12,4
		30	26,5	11,6
		21	29,9	13,4
II	34,1-46,1	25	34,5	14,8	8
		1	35,8	14,9
		19	37,9	17,7
		5	39	16,1
		6	40	16,6
		13	41	17,1
		8	42	17,4
		26	45	18
III	46,1-58,1	7	46,2	18,4	11
		15	46,7	18,6
		29	46,8	18,4
		24	48	18,6
		20	48,3	19,3
		28	48,6	17,8
		23	50,6	20,3
		16	53,8	20,5
		18	54,5	19,9
		22	56	20
		14	57	20,5
IV	58,1-70,1	27	58,4	21	5
		2	65,1	22,2
		12	67	23
		17	67,8	23,2
		11	68,8	22,2
V	70,1-82,1	10	75	24,3	2
		9	82,1	25,2

 

На основе рабочей получаем итоговую группировочную таблицу

 Таблица 2.3

Группировка домохозяйств по валовому доходу в среднем на одного члена домохозяйства

Групп. домохозяйств по валовому доходу в среднем на одного члена домохозяйства, тыс.руб.	Середина интервала xi	Число домохозяйств ni	накопленные частоты S
22,1 – 34,1	28,1	4	3
34,1 – 46,1	40,1	8	12
46,1 – 58,1	52,1	11	23
58,1 – 70,1	64,1	5	28
70,1 – 82,1	76,1	2	30
∑		30

По полученной группировке можно сделать вывод, что наибольшее число домохозяйств (11 из 30) имеют валовой доход от 46,1 до 58,1 тыс.руб.

 

2. Построим графики ряда распределения.

 

График частот ряда распределения

 

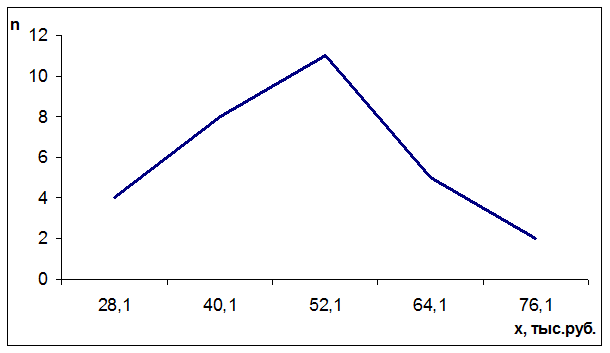
Графически определим значения моды и медианы

 

Мода (наиболее часто встречающееся значение)

Мода находится в интервале от 46,1 до 58,1

Графическое определение моды

Мо

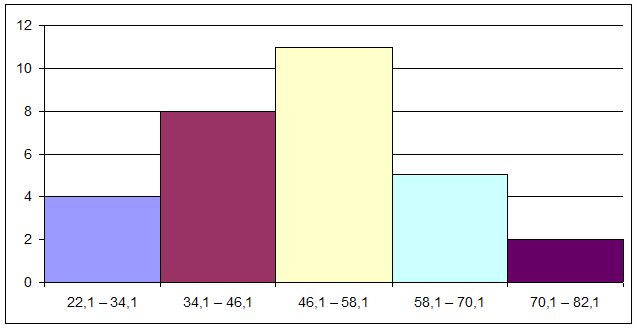
Мо ≈ 49 тыс.руб.

Вывод: наиболее часто встречающееся значение (мода) валового дохода в среднем на одного члена домохозяйства составляет 49 тыс.руб.

 

Медиана (значение признака у средней единицы ранжированного ряда)