Информационной базой для расчета страховых тарифов по страхованию жизни является таблица смертности, которая формируется на основании данных переписи населения.
Определим содержание информации и порядок построения таблицы смертности в табл. 3.
Таблица 3.
Таблица смертности
| Возраст | Число живущих по данным переписи населения | Число смертных случаев по данным переписи | Норма смертности | Живущие | Умершие | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||||||
| 0 | 632698 | 116490 | 0,18412 | 100000 | 18412 | |||||||
| 1 | 522777 | 34338 | 0,06568 | 81588 | 5359 | |||||||
| 2 | 490999 | 13564 | 0,02763 | 76229 | 2105 | |||||||
| И.т.д. |
|
|
|
|
| |||||||
Гр.2 и гр.3 – статистические данные.
Гр.4 = гр.3: гр.2, т.е. 116490: 632698 = 0,18412.
Таблица смертности показывает число умерших из года в год в каждом возрасте из данного числа рождений.
Гр.5 – произвольное число для возраста 0. Часто используется число 100000. Умножением данного произвольного числа (например, 100000) га число в гр. 4 для возраста 0, получаем число умерших до достижения одного года (гр.6). В нашем случае,
гр.6 = 100000 *0,18412 = 18412.
Гр.5 для следующего года определяется разницей значения гр. 5 предыдущего года и гр.6 предыдущего года.
Для расчета страховых тарифов используются общие для населения региона данные, как перепись населения, так и статистическая информация, собранная непосредственно в страховой компании за ряд лет.
При расчете страховых тарифов по страхованию жизни используется технический процент. Сущность технического процента заключается в том, что он представляет собой форму участия страхователя в инвестиционном доходе страховщика. Технический процент определяется с использованием формулы сложных процентов:
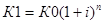, (22)
где i – годичный доход капитала (в страховой териминалогии – норма доходности);
К1, К0 - соответственно накопленный и вложенный капитал.
В страховании решается обратная задача, т.е. требуется определить, какую сумму необходимо вложить в настоящий момент, чтобы по истечении определенного времени (n) получить сумму, равную единице капитала. Таким образом, здесь требуется определить современную стоимость будущего капитала. В этом случае технический процент (дисконтирующий множитель) будет определяться по формуле (23):
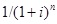(23)
Проиллюстрируем использование технического процента в расчетах.
Определим размер страхового платежа, обеспечивающего через 2 года страховую сумму в 10000 руб. при норме доходности в 9% годовых.
Страховой платеж (С) в этом случае будет определяться:
.
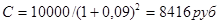Если платеж будет не разовым (единовременным), а ежегодным, т.е. в данном случае будет производиться 2 раза, тогда его можно определить по формуле (7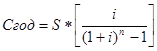.24):
(24)
В нашем случае, Сгод = 10000 * [ 0,09 / (1,09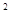 
- 1) ] = 4785 руб.
Страхование жизни обычно осуществляется в двух формах: страхование сумм (капитала) и страхование ренты (аннуитетов). Различия вызваны формой выплат. При страховании капитала выплата производится застрахованному в случае наступления страхового события единовременно в размере страховой суммы. При страховании ренты производятся периодические выплаты. Далее рассмотрим расчеты тарифных ставок по страхованию жизни капитала и страхованию ренты.
Брутто-ставка (Тб) по страхованию жизни определяется так же, как и по рисковым видам страхования по формуле (1).
Рассмотрим порядок расчета нетто-ставки по страхованию жизни (капитала) при помощи таблицы смертности и таблицы коммутационных чисел.
Определение нетто-ставки (Тн-с) осуществляется по формуле (25):
(25.)
где –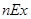 
единовременная ставка на дожитие для застрахованного возраста 
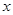х лет со сроком страхования 
лет;
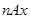- единовременная ставка на случай смерти для застрахованного возраста 
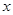х лет со сроком страхования 
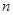лет.
Такая структура тарифной ставки объясняется наличием двух страховых случаев в классическом страховании жизни.
Определение нетто-ставки возможно двумя способами: при помощи таблицы смертности, а также при помощи таблицы коммутационных чисел.
А) Определим нетто-ставку при помощи таблицы смертности. Сначала рассчитаем единовременную ставку на дожитие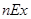 
. Для этого используется формула (26):
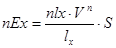, (26)
где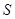 
– страховая сумма, которая традиционно в рассматриваемых расчетах принимается за 100 руб.;
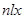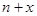– число доживающих до возраста 
;
- число доживающих до возраста ;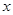
V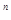 
- дисконтирующий множитель, размер которого зависит от нормы доходности по страхованию жизни, определяется по формуле 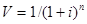(27).
(27)
Рассмотрим пример расчета. Используем следующие данные, занесенные в таблицу смертности (см. табл. 4.).
Таблица 4.
| Возраст х | Число доживающих
до возраста х
| Число умирающих при
переходе от возраста х
к возрасту х+1
|
| 0 | 100000,0 | 4060,0 |
| 1 | 95940,0 | 860,0 |
| … | …. | … |
| 20 | 92917,0 | 150,0 |
| … | … | … |
| 40 | 88565,0 | 319,0 |
| 41 | 82246,0 | 336,0 |
| 42 | 87910,0 | 352,0 |
| 43 | 87558,0 | 369,0 |
| 44 | 87189,0 | 384,0 |
| 45 | 86805,0 | 400,0 |
| … | … | … |
| 60 | 76693,0 | 1099,0 |
Для застрахованного возрастом 40 лет при сроке страхования 5 лет и норме доходности 3% годовых единовременная ставка на дожитие составит:
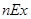= (86805,0 * 0,86261)/ 88565,0 * 100 = 84,55 руб. со 100 руб. страховой суммы.
Рассчитаем единовременную ставку на случай смерти ( 
) по формуле (28):
(28)
– число умирающих при переходе от возраста 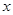к возрасту 
.
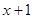В случае, если застрахованному 40 лет и срок страхования 5 лет, ставка на случай смерти составит:
40А5 = (319*0,97087 + 336*0,94260 + 352*0,91514 + 369*0,88849 + 384*0,86261)\88565,0*100 = 1,82 руб. со 100 руб. страховой суммы.
Таким образом, тарифная нетто-ставка (Тн-с) в рассматриваемом примере составит 86,37 руб. со 100 руб. страховой суммы или 86,37%.
В практике страхования единовременные ставки применяются достаточно редко. Чаще всего условия страхования предусматривают внесение страхователем периодических страховых взносов, скажем ежегодных. Чтобы получить годовые взносы, нельзя просто поделить единовременный взнос на соотвествующее количество лет страхования, т.к. необходимо учитывать потерю на доходах от инвестирования временно свободных средств, а также уменьшение числа застрахованных вследствие смертности, поэтому применяют так называемые коэффициенты рассрочки 
(29).
(29)
Для получения годичной тарифной ставки следует ее единовременное значение разделить на коэффициент рассрочки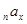 
.
Б) Рассчитаем нетто-ставку при помощи таблицы коммутационных чисел.
Сначала определим значения коммутационных чисел. Коммутационные числа представляют собой математическую комбинацию данных таблицы смертности и служат для упрощения, не имея при этом конкретного экономического смысла.
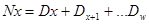
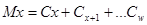
где 
– последнее значение таблицы коммутационных чисел.
В обозначениях коммутационных чисел формулы для определения нетто-ставок на дожитие и на случай смерти выглядят таким образом:
- единовременная ставка на дожитие (30)
- единовременная ставка на случай смерти (31)
При расчете тарифных ставок с использованием коммутационных чисел можно использовать специальные формулы (32), (33) для расчета годичных взносов:
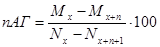(32)
где 
-годичный взнос на случай смерти страхователя возраста 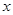лет на 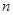лет.
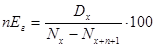(33)
где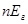 
годичный взнос на дожитие страхователя возраста х лет на n лет.
Рассмотрим порядок расчета нетто-ставки по страхованию жизни с условием выплаты ренты.
Для определения страховых тарифов с условием выплаты ренты используются формулы аннуитетов. Для расчета используют коммутационные числа. Методика расчета исходит их того, что страхование с условием выплаты ренты представляет собой своего рода последовательное повторяемое страхование на дожитие:
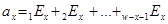(34)
Определим различные виды аннуитетов для застрахованного возрастом х при ежегодной выплате ренты в 1 руб. в табл.
Таблица 5.
Формулы для расчета страхового тарифа по страхованию жизни с условием выплаты ренты
| Вид аннуитета | Немедленные пожизненные | Отложенные на п лет пожизненные | Ограниченные на t лет немедленные | Ограниченные на t лет отложенные на n лет |
| Пренумрандо |  ,
Если выплаты
производятся
m раз в году:
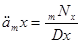m=12
|  ,
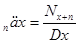Если выплаты
производятся
m раз в году:
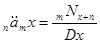m=12
| 
| 
|
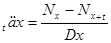
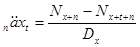
| Постнумерандо |  ,
Если выплаты
производятся
m раз в году:
m=12
|  ,
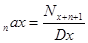Если выплаты
производятся
m раз в году:
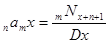m=12
| 
| 
|
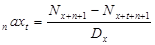
[1 стр. 45 - 67]
Заключение.
На всем протяжении расчётно – графической работы исследовались проблемы, связанные с такой экономической категорией как страхование, которые существовали, существуют и будут существовать, пока в нашей стране не появятся высококвалифицированные кадры, которые бы действительно улучшили сложившуюся экономическую ситуацию в стране, смогли бы информировать население о сущности страхования и о выгодности страховаться.
Сущность страхования в условиях рынка состоит в научной постановке целей и применении средств их реального достижения. На этот вопрос можно посмотреть с разных сторон. Со стороны страхователя главной целью является защита от экономических рисков, ну а цель любой коммерческой организации, каковыми являются, большинство страховщиков является получение прибыли.
Назначение страхования заключается в соглашении между страховщиком и страхователем на основе договора или закона о защите имущественных интересов застрахованного.
В настоящее время страховой рынок в России практически не развит.
Страхование способствует минимизации риска в экономике. Но страховой бизнес сам существует в условиях неопределенности. Страховщики должны быть готовы к тому, что как правило, добровольно себя страхует лицо, предполагающее наступление страхового события, и целью страхования для любого рационального страхователя является превышение суммы, полученной как возмещение ущерба, над страховыми взносами.
Важной проблемой является асимметрия информации между страхователями и страховщиками. Клиенты-страхователи знают значительно больше о состоянии объекта страхования (к примеру, о собственном стиле вождения автомобиля при страховании гражданской ответственности, о состоянии своего здоровья при медицинском страховании). Возникает ситуация неблагоприятного отбора (adverse selection), когда добровольно страхуется скорее водитель-лихач или человек со слабым здоровьем, который надеется за счет медицинской страховки покрыть дорогостоящее лечение.
Другой проблемой является возможность оппортунистического поведения, когда одна сторона сделки пытается извлечь выгоду из недостаточной формализации контракта, нанося ущерб интересам другой стороны. Например, если это не оговорено в договоре страхования, желающий получить страховое вознаграждение водитель будет выбирать более агрессивный (аварийноопасный) стиль вождения, поскольку сложно определить, является ли авария следствием лихачества водителя или неблагоприятных погодных условий. Аналогично, в случае с медицинской страховкой корыстный страхователь будет меньше беречься от простуды (например, ходить в холодную погоду без шапки), если данные обстоятельства, приведшие к наступлению страхового события, не прописаны в страховом контракте и наступление события выгодно страхователю. Страховщику сложно отделить, в каком случае возникновение страхового случая связано с объективными обстоятельствами (действиями сил природы и т.п.), а в каком связано с «коварством» страхователя.
Неопределенность, связанная с асимметрией информации перед заключением страхового соглашения и возможностью оппортунистического поведения после его заключения, сильно тормозит развитие страхования. Страхователи, реагируя на фактические и потенциальные потери, закладывают их в страховые тарифы. Это наиболее неэффективно для общества в ситуации обязательного страхования, поскольку выгоды «хитрых» страхователей должны оплачивать повышенными платежами «простодушные» клиенты.
По мере укрепления и роста рынка страховых услуг, конкуренция в страховом деле будет нарастать и обостряться. Компании вынуждены будут следовать главному принципу конкуренции на рынке: побеждает тот, кто предлагает клиенту наиболее выгодные условия страхования.
Система страхования должна быть простой, понятной и максимально выгодной как для страхователя, так и для страховщика. В этом, главный критерий экономических, юридических и организационных усилий страны, по формированию эффективного страхового механизма и страхового рынка, соответствующего лучшим мировым стандартам страхового дела.
Список использованной литературы.
1. Гвозденко А. А. «Основы страхования». Москва: «Финансы и статистика», 1995 г.
2. Клоченко Л. Н., Пылов К. И. «Основы страхового дела». Ярославль, 2002 г.
3. Колпакова Г. М. «Финансы, денежное обращение, кредит». Москва: «Финансы и статистика», 2004 г
4. Сплетухов Ю. А. , Дюжиков Е. Ф. «Страхование». Москва: ИНФРА-М, 2005.
5. «Финансы» по ред. В. В. Иванова, В. В. Ковалёва. Москва, 2004 г.
6. «Финансы» под ред. В. М. Родионовой. Москва: «Финансы и статистика», 1995 г.
7. Шахов В. В. «Введение в страхование». Москва: «Финансы и статистика», 1998 г.
Дата: 2019-12-22, просмотров: 216.
