Определим приведенный момент сил сопротивления, для всех по­ложений механизма

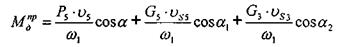
где Р₅ — силы сопротивления пуансона 5 определяем по диа­грамме приведенной в силовом расчете в зависимости от пути и мах си­лы сопротивления;

G - силы тяжести звеньев 3 и 5

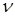— скорости точки приложения силы Р₅ и G;

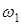 = 13,61 рад/с — угловая скорость входного звона;  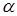  — угол между векторами Р₅ (G) и v;

Угол а и си на такте холостого хода равны 180°, а на рабочем ходу рав­ны 0°.

Таблица 3

Расчетная таблица определения приведенного момента сил сопротив­ления

№ положения	Сила со­противле­ния Р3/Рмах	Сила со­противле­ния Р5, Н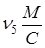
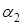
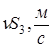
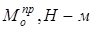
0	0	0	0	0	0	0
1	0	0	0,58	7,6	0,79	10,98
2	0	0	1,09	3,7	1,46	20,46
3	1	730	1,19	1,6	1,6	86,27
4	0,48	350,4	0,81	6,4	1,1	36,17
5	0	0	0	0	0	0
6	0	0	0,31	171,5	0,4	-5,62
7	0	0	0,66	173,7	0,88	-12,31
8	0	0	0,85	177,2	1,15	-16,1
9	0	0	0,88	178,8	1,19	-16,67
10	0	0	0,76	175	1,02	-14,28
11	0	0	0,45	171,2	0,63	-8,68

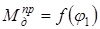По вычисленным значениям строим диаграмму в мас­штабе μ_М =0,5 Н-м/мм. Методом графического интегрирования строим диаграмму работ сил движущих. Для этого выбираем полюсное расстоя­ние Н=30 мм Через середины интервалов 0—1, 1—2 ... ... 23—24 прово­дим перпендикуляры к оси абсцисс (штриховые линии).

Точки пересечения этих перпендикуляров с диаграммой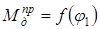

проецируем на ось ординат и соединяем найденные точки 1', 2'... 6' и т. д. с полюсом р (точки 1', 2 , 3', 4', 5' слились в одну). Из начала коорди­нат диаграммы 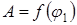проводим прямую, параллельную лучу р—1', получаем точку 1". Из точки 1" проводим прямую 1"—2", параллельную лу­чу р—2'... (8^м—9^м)" \\(р—9') и т. д. Масштаб диаграммы работ определяем по формуле:

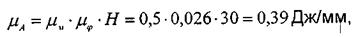
где

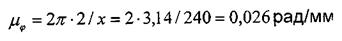
Так как 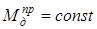то диаграмма работ 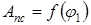есть прямая линия.
Кроме того, при установившемся движении за цикл, работа движущих
сил равна работе всех сопротивлений. На основании вышеизложенного
соединяем начало координат О диаграммы A(φ) с точкой 24" прямой линией, которая и является диаграммой 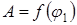.        Если графически про­
дифференцировать эту диаграмму, то получим прямую, параллельную
оси абсцисс. Эта прямая является диаграммой приведенных моментов
сил полезного сопротивления .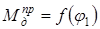

Для построения диаграммы приращения кинетической энергии машины 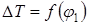следует вычесть алгебраически из ординат диаграммы
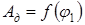ординаты диаграммы 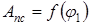т.е. ординаты 1—1*, 2—2*, ..., 10—10* ... 12—12*, 13—13* и т. д. Диаграммы  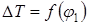равны соответственно ординатам 1^м—1° 2^м—2° .. 10"—10°... 12"—12°, 13"—13°, диаграммы .

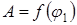3.2. Построение диаграмм кинетической энергии, приведенно­го момента инерции звеньев механизма и энергомасс. Опре­деление момента инерции маховика

Кинетическая энергия механизма равна сумме кинетических энер­гий его звеньев, т. е. Т = Т₁ + Т₃ + Т₅                                      |

где Т₁ = 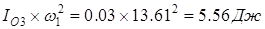— величина постоянная во
всех положениях механизма;

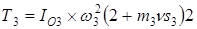Дж — кинетическая энергия кулисы 3;

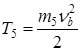— кинетическая энергия пуансона 5.

Приведенный момент инерции звеньев механизма вычисляем по формуле 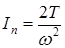 и полученные результаты сводим результаты в табл. 4.

Таблица 4

Значения кинетической энергии и приведенного момента инерции звеньев механизма

По­ложе­ние	Т3, Дж	Т5,Дж	Т,Дж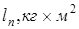
0	0	0	5,56	0,06
1	7,13	1	13,69	0,142
2	15,09	3,56	24,21	0,261
3	21,9	4,25	31,71	0,342
4	14,5	1,97	22,03	0,238
5	0	0	5,56	0,06
6	3,31	0,29	9,16	0,099
7	8,12	1,31	14,99	0,162
8	11,13	2,17	18,86	0,204
9	11,64	2,32	19,52	0,211
10	9,65	1,73	16,94	0,183
11	5,47	0,61	11,64	0,126

Строим диаграмму приведенного момента инерции 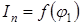построенной в масштабе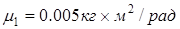

Строим диаграмму энергомасс, исключая параметр 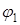 из диаграмм и 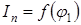. Для этого строив прямоугольную систему координат 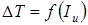. Из начала координат проводим прямую под углом 45° к оси I_n. Точки 1¹, 2', 3'... 23' диаграммы  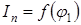проецируем на эту прямую и далее до пересечения с прямыми, проведенными из точек 1*, 2*, 3*... 23* диа­граммы 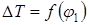. Соединяем точки пересечения О, 1, 2 ... 23 плавной кри­вой. По заданному коэффициенту неравномерности движения δ и средней угловой скорости  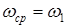определяем углы ψ_тахи ψ_min по формулам:

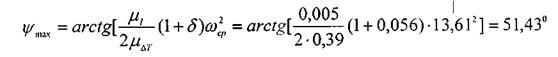
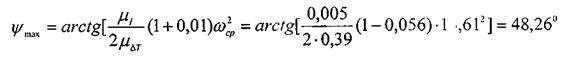
К диаграмме энергомасс  проводим две касательные под уг­лами ψ_тахи ψ_min . Эти касательные отсекут на оси ординат с отрезок KL, ко­торый определяет кинетическую энергию маховика в масштабе . Вычисляем момент инерции маховика по формуле:

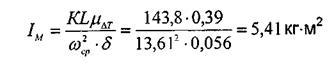
Определяем диаметр маховика, его массу и ширину.

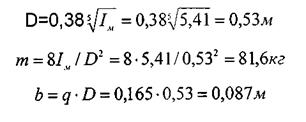
СПИСОК ЛИТЕРАТУРЫ

1. Артоболевский И .И. Теория машин и механизмов. М.: Наука, 1975.

2. Безвесельный К.С. Вопросы и задачи по теории механизмов и машин. Киев: Вища школа, 1977.

3. Методические указания по изучению дисциплины и выполнению курсового проекта. Москва 1989г.

4. Юдин В.А., Петрокас Л.В. Теория механизмов и машин. М.: Высшая школа, 1981.