Для определения степеней свободы плоских механизмов применяем формулу П. Л. Чебышева:
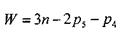 i
i
Для нашего механизма имеем:
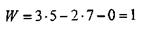
Произведем разбиение механизма на простейшие структурные формы. Произведем расчленение механизма на группы Асура. Механизм состоит из:
- одной группы Ассура II класса, 2-го вида (звенья 4-5);
- одной группы Ассура II класса, 3-го вида (звенья 2-3);
- одного механизма I класса состоящего из входного звена 1 и стойки 6.
 1.3. Построение схемы механизма
1.3. Построение схемы механизма
Построение проводим в масштабе длин 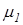 [м/мм]. Длина кривошипа на чертеже ОА=83,7 мм. Тогда масштаб длин определяем по формуле:
[м/мм]. Длина кривошипа на чертеже ОА=83,7 мм. Тогда масштаб длин определяем по формуле:
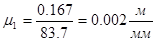
Вычерчиваем кинематическую схему механизма. Для построения 12 положений звеньев механизма разделив траекторию описываемую точкой А кривошипа ОА на 12 частей. Из точки О3 проводим линии длиной равной длине звена 3 через отмеченные на окружности точек А0, А1, ... А11, затем намечаем линию движения пуансона 5 точки В0 B1, B2 ...В11.
1.4. Построение планов скоростей механизма
Планом скоростей механизма называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек звеньев механизма в данный момент
Определим скорость точки А звена ОА:
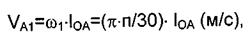
где 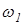 - угловая скорость кривошипа ОА, С1; IOA- длина кривошипа ОА, м
- угловая скорость кривошипа ОА, С1; IOA- длина кривошипа ОА, м
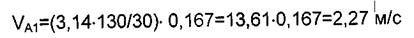
Построение плана скоростей начинаем от входного звена, т. е. кривошипа ОА. Из точки р, откладываем в направлении вращения кривошипа ОА вектор скорости точки А: ра=85,2 мм.
Масштаб плана скоростей находим по формуле:
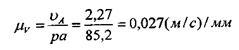
Построение плана скоростей группы Ассура II класса 3-го вида (звенья 2 и 3) производим по уравнению: VA3O3 = VA2 + VA2A3
 где vА3О3 - скорость точки А кулисы О3А;
где vА3О3 - скорость точки А кулисы О3А;
VA2 - скорость точки А звена 2 во вращательное движении относительно точки О направлена параллельно оси звона ОАVA2 = 0;
\/A2A3 - скорость точки А кулисы 3, направлена вдоль оси О3А.
Из точки а проводим линию, параллельную оси звена О3А, а из полюса р плана скоростей - линию, перпендикулярную ocи O3A. Точка а3 пересечения этих линий дает конец вектора искомой скорости VA3.
Скорости центра тяжести кулисы S3 и звена 4 определяем по правилу подобия. Найденные точки S3 и 4 соединяем с полюсом р.
Построение плана скоростей группы Ассура II класса 2-го вида (звенья 4 и 5) производим по уравнению:
VB = V4+V4B, где VB - скорость точки В пуансона 5.
V4 - скорость точки 4 расположенной на звене 3 во вращательном движении относительно точки О3 направлена параллельно оси звена О3А;
V4B - скорость звена 4В, направлена перпендикулярно оси 4В.
Из точки 4 проводим линию, перпендикулярно оси звена 4В, а из полюса р плана скоростей - линию, перпендикулярную оси 4В. Точка b пересечения этих линий дает конец вектора искомой скорости VB.
Истинное значение скорости каждой точки находим по формулам:
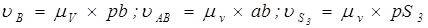
Определяем угловую скорость кулисы АО3 для 12 положений по формуле и сводим полученные данные в таблицу 2.
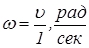
Таблица 2
 Значение скоростей точек кривошипно-ползунного механизма в м/с
Значение скоростей точек кривошипно-ползунного механизма в м/с
и угловых скоростей шатунов в рад/с
| Параметр
| Номер положения механизма
|
| ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 0 | |
| VB =VS5 | 0,58 | 1,09 | 1,19 | 0,81 | 0 | 0,31 | 0,66 | 0,85 | 0,88 | 0,76 | 0,45 | 0 |
| VB а4 | 0,08 | 0,07 | 0,03 | 0,09 | 0 | 0,05 | 0,07 | 0,04 | 0,02 | 0,07 | 0,06 | 0 |
| v ОА | 1,2 | 2,09 | 2,26 | 1,62 | 0 | 0,69 | 1,63 | 2,18 | 2,28 | 1,91 | 1,11 | 0 |
| VS3 | 0,79 | 1,46 | 1,6 | 1,1 | 0 | 0,4 | 0,88 | 1,15 | 1,19 | 1,02 | 0,63 | 0 |
| V3 2а3 | 1,97 | 0,97 | 0,42 | 1,63 | 2,3 | 2,19 | 1,62 | 0,71 | 0,31 | 1,28 | 2,01 | 2,3 |
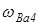
| 0,498 | 0,436 | 0,187 | 0,56 | 0 | 0,311 | 0,436 | 0,249 | 0,124 | 0,436 | 0,373 | 0 |
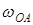
| 1,22 | 2,26 | 2,47 | 1,7 | 0 | 0,62 | 1,37 | 1,76 | 1,83 | 1,57 | 0,96 | 0 |
1.5. Построение планов ускорений механизма
Планом ускорений механизма называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению ускорениям различных точек звеньев механизма в данный момент, называют планом ускорений механизма.
Построение плана ускорений по следующей схеме: Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А звена ОА будет иметь только нормальное ускорение, величина которого равна
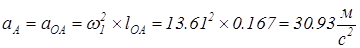
Определяем масштаб плана ускорений
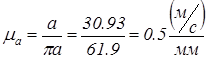
где 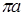 = 61,9 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки А кривошипа ОА
= 61,9 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки А кривошипа ОА
Из произвольной точки п — полюса плана ускорений проводим вектор па параллельно звену ОА от точки А к точке О.
Построение плана скоростей ускорений группы Ассура II класса 3-го вида (2-3 звено) проводим согласно уравнений:
 где
где 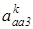 — кариолиосово ускорение;
— кариолиосово ускорение;
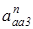 — нормальное ускорение точки А3 кулисы 3 в ее вращательном движении относительно точки О3;
— нормальное ускорение точки А3 кулисы 3 в ее вращательном движении относительно точки О3;
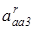 — относительное ускорение поступательного движения
— относительное ускорение поступательного движения
кулисы 3 относительно камня А2;
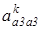 — тангенциальное ускорение точки А3 кулисы 3 в ее
— тангенциальное ускорение точки А3 кулисы 3 в ее
вращательном движении относительно точки О3;
Для определения направления кариолисова ускорения необходимо вектор относительной скорости Va3a2 повернуть на 90° в направлении угловой скорости кулисы 3.
Найдем величины ускорений 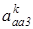 и
и 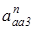
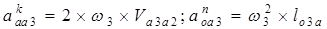
Построение плана ускорений группы Ассура II класса 2-го вида ( звено 4-5) проводим согласно уравнению: 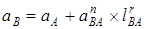
где ав— ускорение точки В, направлено вдоль оси АБ;
аВА - нормальное ускорение точки В при вращении его вокруг точки А, направлено вдоль оси звена АВ от точки В к точке А.
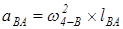
 — касательное ускорение точки В при вращении его вокруг точки А (величина неизвестна) направлено перпендикулярно к оси звена В0В5
— касательное ускорение точки В при вращении его вокруг точки А (величина неизвестна) направлено перпендикулярно к оси звена В0В5
Из точки 4 вектора 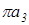 плана ускорений проводим прямую, параллельную оси звена ВА, и откладываем на ней в направлении от точки В к точке А отрезок аВА. Через конец вектора АВА проводим прямую, перпендикулярную к оси звена ВА произвольной длины. Из полюса
плана ускорений проводим прямую, параллельную оси звена ВА, и откладываем на ней в направлении от точки В к точке А отрезок аВА. Через конец вектора АВА проводим прямую, перпендикулярную к оси звена ВА произвольной длины. Из полюса 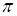 проводим прямую, параллельную оси В0В5.
проводим прямую, параллельную оси В0В5.
Точка b пересечения этих прямых определит концы векторов ab и 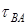 . Складывая векторы пвд |i tba. получаем полное ускорение звена АВ, для этого соединяем точки 4 и b прямой. Точки центра тяжести элементов на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков.
. Складывая векторы пвд |i tba. получаем полное ускорение звена АВ, для этого соединяем точки 4 и b прямой. Точки центра тяжести элементов на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков.
 Численные значения ускорений всех точек механизма, а также касательные ускорения для седьмого положения механизма найдем по формулам:
Численные значения ускорений всех точек механизма, а также касательные ускорения для седьмого положения механизма найдем по формулам:
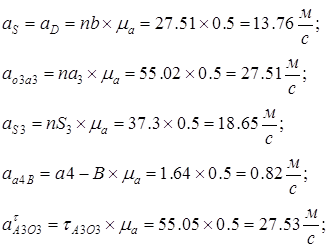
1.6. Построение годографа скорости центра масс кулисы 3 и кинематических диаграмм точки В пуансона 5
Для построения годографа скорости переносим векторы pS3 параллельно самим себе своими началами в одну точку p, называемую полюсом. Соединяем концы векторов плавной кривой.
Для построения диаграммы перемещения точки В пуансона откладываем по оси абсцисс отрезок длиной 288 мм, изображающий период Т одного оборота кривошипа, и делим его на 12 равных частей. От точек 1, 2... ...11 схемы положений механизма откладываем ординаты 1—1, 2—2..., 11—11, соответственно равные расстояниям В0—В1, В0—В2... В0— В12,-проходимые точкой В от начала
отсчета.
Вычисляем масштабы диаграммы перемещения:
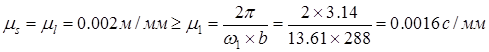
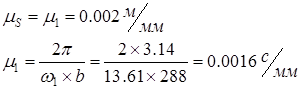
Диаграмма скорости точки В строится графическим дифференцированием графика перемещения по методу хорд. Криволинейные yучастки графика перемещения точки В заменяем прямыми 0—1, 1—2... 11 – 12.
 12. Под графиком перемещения проводим прямоугольные оси V и t. K оси t выбираем полюсное расстояние К=36 мм. Из полюса проводим наклонные прямые параллельные хордам 0—1, 1—2 .. .11—12. Из середины интервалов 0—1, 1—2 ... 11—12 проводим перпендикуляры к оси t (штриховые линии). Из точек 1, 2... 12 проводим прямые, параллельные оси t. Точки пересечения соединяем плавной кривой.
12. Под графиком перемещения проводим прямоугольные оси V и t. K оси t выбираем полюсное расстояние К=36 мм. Из полюса проводим наклонные прямые параллельные хордам 0—1, 1—2 .. .11—12. Из середины интервалов 0—1, 1—2 ... 11—12 проводим перпендикуляры к оси t (штриховые линии). Из точек 1, 2... 12 проводим прямые, параллельные оси t. Точки пересечения соединяем плавной кривой.
Масштаб диаграммы скорости вычисляем по формуле:
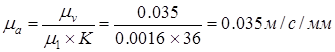 |
Диаграмма ускорения точки В строится графическиm дифференцированием диаграммы скоростей. Все построения аналогичны ранее описанным при графическом дифференцировании диаграммы перемещения.
Масштаб диаграммы ускорения равен:
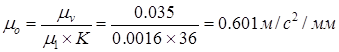 |
Дата: 2019-12-22, просмотров: 339.