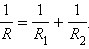Проводники в электрических цепях могут соединяться последовательно и параллельно.
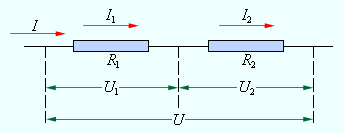
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
| I1 = I2 = I. |
|
| Рисунок 1.9.1. Последовательное соединение проводников |
По закону Ома, напряжения U1 и U2 на проводниках равны
| U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
| U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
|
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
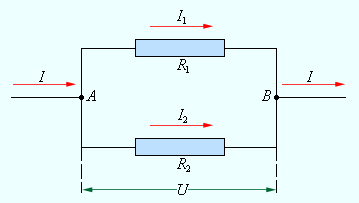
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
| U1 = U2 = U. |
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
| I = I1 + I2. |
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
|
| Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
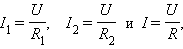
|
где R – электрическое сопротивление всей цепи, получим
|
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
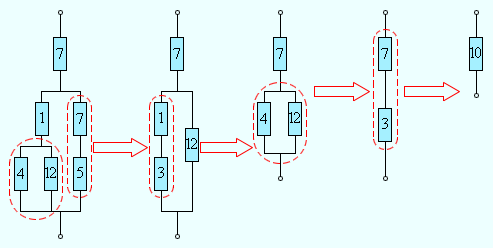
|
| Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом) |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
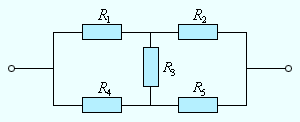
|
| Рисунок 1.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников |
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
Дата: 2019-12-10, просмотров: 376.