Математическая логика с развитием ВТ оказалась в тесной взаимосвязи с вопросами конструирования и программирования ВТ. Алгебра логики нашла широкое применение первоначально при разработке релейно-контактных схем. Первым фундаментальным исследованием, обратившим внимание инженеров, занимавшихся проектированием ЭВМ, на возможность анализа электрических цепей с помощью булевой алгебры была опубликованная в декабре 1938 года статья американца Клода Шенона «Символический анализ релейно-контактных схем» После этой статьи проектирование ЭВМ не обходилось без применения булевой алгебры. Роль ключа в схемах вначале играли электромеханическое реле, затем использовались электронные лампы и транзисторы.
Использование контактных элементов для построения логических схем ЭВМ не оправдало себя ввиду низкой надежности, больших габаритов, большого энергопотребления и низкого быстродействия.
Развитие технологии позволило объединить несколько логических элементов на одной интегральной схеме. Появление электронных приборов (вакуумных и полупроводниковых) создало возможность построения логических элементов с быстродействием от 1 миллиона переключений в секунду и выше.
Логическая схема строится на основе объединения электронных элементов. Эти элементы реализуют конкретные логические операции и носят название ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ. На вход каждого элемента подаются сигналы, называемые входными. На выходе получаем выходной сигнал. Если есть сигнал - значит 1, если нет сигнала – 0. каждая логическая схема реализует определенную логическую функцию, а при подаче на её вход строго определенной комбинации входных сигналов мы должны получить на выходе вполне определенный результат – 0 или 1.
Логический элемент - это схема реализующая логические операции И, ИЛИ, НЕ.
Рассмотрим логические элементы, реализующие основные логические операции.
ИНВЕРТОР – реализует операцию отрицания, или инверсию. В схемах изображается следующим образом:



 Х Х
Х Х
У инвертора один вход и один выход. Сигнал на выходе появляется тогда, когда на входе его нет, и наоборот.
КОНЬЮНКТОР – реализует операцию коньюнкции. В схемах изображается следующим образом:
|
 |


 Х2 Х1 ^ X2 ^ X3…
Х2 Х1 ^ X2 ^ X3…
Х3
У коньюнктора один выход и не менее двух входов. Сигнал на выходе появляется тогда и только тогда, когда на все входы поданы сигналы.
ДИЗЬЮНКТОР – реализует операцию дизьюнкции. В схемах изображается следующим образом:

|


 Х2 Х1 \/ Х2 \/ Х3 ….
Х2 Х1 \/ Х2 \/ Х3 ….
Х3
У дизьюнктора один выход и не менее двух входов. Сигнал на выходе не появляется тогда и только тогда, когда на все входы не поданы сигналы.
Логические элементы, реализующие операции И, ИЛИ, НЕ, называются основными логическими элементами, та как с их помощью можно реализовать в виде логической схемы любую логическую функцию.
 F(X,Y,Z) = X ^(Y \/Z)
F(X,Y,Z) = X ^(Y \/Z)

 Х У Z
Х У Z






|





|
 Х Х
Х Х
 F
F
У Y \/ Z
Z
Итак, процесс построения функциональных схем для разработки устройств ПК можно описать следующим образом:
1. На основе анализа функции, которое реализует устройство, составляется таблица истинности.
2. По этой таблице при помощи описанного ниже метода находят логическую функцию.
3. Производится минимизация логической функции.
4. По упрощенной логической функции строится функциональная логическая схема устройства.
Упражнение 1. Постройте схему на логических полупроводниковых элементах, соответствующих логической формуле F(X,Y,Z) = (X и Y) или Z.
Решение.




|


|
 Х
Х
X и У S= (X и У) или Z = F(X,Y,Z)
 У
У
Z
Входные сигналы Х, У, Z. Сигналы Х, У поступают на вход элемента и, с выхода и сигнал поступает совместно с сигналом Z на вход элемента или.
Выходной сигнал S =(Х и У) или Z соответствует заданной логической функции.
Упражнение 2. Постройте схему, работа которой описывается логической формулой F(X,Y,Z) = (X и У и Z) или неZ.
Решение.
|
|









 уХ X и Y и Z S = (X и Y и Z) или неZ = F(X,Y,Z)
уХ X и Y и Z S = (X и Y и Z) или неZ = F(X,Y,Z)
 |
z неZ
Входные сигналы Х,У,Z подаются на вход схемы и. Сигнал Z поступает на вход инвертора, на выходе неZ. Сигналы с выхода схем и и не подаются на схему или. Выходной сигнал S = (X и У и Z) или неZ.
Задача
1. Запишите логическую формулу, описывающую состояние схемы:
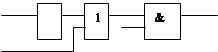 |
Х
 |
У
 Z
Z
2. Постройте схемы, работа которых описывается логическими формулами:
а) F(A,B,C) = (A и В) или (В и С);
б) F(Х,У) = (X или У) и неУ;
Задания
1. Запишите логическую формулу описывающую состояние схем:
а) б)

|
|

|
 А
А





 Х В
Х В








|

|

 Z D
Z D
2. Постройте схемы работа которых описывается логическими формулами.
а) F(A,B,C,F) = (A или В) и С и (В или F);
б) F(A,B,C,F) = (A или В) или (С и (В или F));
Задачи 1. В предложенных схемах запишите формулы выходных сигналов каждого логического элемента:
| ||||
 | ||||

















|
|
|
|
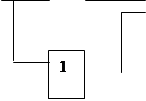 |  | ||||
 | |||||

 У
У
У
Z
|
|



|
|
 Х г) У
Х г) У












 в)
в)




У
Z
 Z
Z
|
|
|






 ж) Х
ж) Х

 У
У
 Z
Z
Задача 2. Постройте схему работа которой описывается логической формулой
F(A,B,C,D,F) = (C и D и А) или (В и F);
|
|
 Задачи 3. Запишите логическую формулу, описывающую состояние схемы, составьте таблицы истинности: Х
Задачи 3. Запишите логическую формулу, описывающую состояние схемы, составьте таблицы истинности: Х



|
|
 Х б)
Х б)












 А)
А)
 | ||
 | ||
 У У
У У
 Z Z
Z Z


|
|









|

|



 У
У
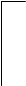
 У
У
 |  |
 Z
Z
Z











|
|
| |
Используя законы логики, упростите ее. Правильность преобразования проверьте таблицей истинности.


















 Задача 5. Два друга собрали схему. В результате тестирования (проверки выходного сигнала от всевозможных комбинаций входных) оказалось, что выходной сигнал D в точности повторяет один из трех входных. Укажите какой.
Задача 5. Два друга собрали схему. В результате тестирования (проверки выходного сигнала от всевозможных комбинаций входных) оказалось, что выходной сигнал D в точности повторяет один из трех входных. Укажите какой.
|


|
 B
B
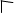 |


|

|

Составление логических схем по заданным таблицам.
Правило составления остается таким же, как при работе с контактными схемами.
Упражнение 1. По заданным таблицам истинности запишите функцию, составьте логические схемы.
а) б)
| а | в | F(а, в) |
| А | В | F(А,В) |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 |
Решение.
А) Берем строки, в которых F(A, B) = 1. Это вторая и третьи строки.
F(A,B) = (A и не В) или (не А и В)
Упростить формулу нельзя. Проверим правильность полученной формулы по таблице истинности, в которую записываются значения промежуточных сигналов.
| А | В | неА | неВ | А и неВ | неА и В | F(A, B) |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Значения F(A, B) в полученной и исходной таблицах совпадают при одних и тех же значениях входных сигналов, следовательно, формула верна. Строим схему:








|









|

|
 А неА неА и В
А неА неА и В
А и неВ
В неВ
Б) Для записи формулы выходной функции f(A,B) берем первую, вторую, четвертую строки таблицы, в которой F(A,B) = 1. F(A, B) =(А и В) или (неА и В) или (неА и неВ). Используя законы логики, упростим выражение: F(А,В) = (А и В) или (неА и (В или неВ) = (А и В) или неА и 1 = (А и в) или неА = (А или неА) и (В или неА) = 1 и (В или неА) В или неА. Формула выходной функции по заданной таблице F(А,В) = В или неА. Проверим её таблицей истинности:
| А | В | неА | F(А,В) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 |
Полученная таблица совпадает с исходной по значениям входных сигналов А, В и соответствующим им выходных. Строим схему:



|
 А неА В или неА
А неА В или неА
 |
Задача 1.В комнате три выключателя - А, В, С:
А – при входе
В – над письменным столом;
С – над диваном.
Постройте схемы, которые позволяют включать свет следующим образом:
любым из следующих включателей
одновременно включением А и В или только С;
одновременно включением всех трех.


































 Задача 2. В формуле, описывающей схему, допущены ошибки, исправьте их, упростите схему:
Задача 2. В формуле, описывающей схему, допущены ошибки, исправьте их, упростите схему:
Х Z
У неХ
Z неZ
неУ
F(X,Y,Z) = ((X или У) или (Z или неХ)) и (У и (неZ и неУ)).
Задача 4 Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):
 |  |
 А В С А
А В С А







 1 0 0 В
1 0 0 В
 0 1 0 С
0 1 0 С

 1 1 1
1 1 1
Задание
а) б)
|
| ||||||||
 |  |  | |||||||
X
















|
 x ch
x ch
|
У Y


 Z Z
Z Z
в)
 | |||
|
X





 Y
Y
Задача 2. Судейская коллегия состоящая из трех членов, выносит решение большинством голосов при тайном голосовании. Постройте такую схему, чтобы голосование каждого члена «за» производилось нажатием кнопки (включением выключателя) и в случае принятия решения загоралась сигнальная лампа.
Задача 3. Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):



 А неА В С
А неА В С
1 0 1 0
0 1 0 0
1 0 1 1
Законы логики
Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной короткой и понятной форме.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания.
Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.
Законы логики
| № п/п | Закон логики | Математическая запись | Название закона |
| 1 | А = А(А=А) | Закон тождества | |
| 2 | __ А & А = 0 | __ А * А = 0 | Закон непротиворечия |
| 3 | __ А v A = 1 | __ A + A = 1 | Закон исключающего третьего |
| 4 | == А = А | Закон двойного отрицания | |
| 5 | А & 0 = 0; A v 0 = A | А * 0 = 0; А + 1 = А | |
| 6 | A & 1 =A; A v 1 = 1 | A * 1 = A; A + 1 = 1 | |
| 7 | A & A = A; A v A =A | A * A =A; A + A =A | |
| 8 | __ A v A =1 | __ A + A =1 | Законы Моргана |
| 9 | ________ __
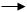 (A B) =A & B (A B) =A & B
| ||
| 10 | __
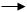 A B = A v B A B = A v B
| ||
| 11 | A & (A v B) = A | A * (A + B) = A | Закон поглощения |
| 12 | A v A & B =A | A + A * B =A | Закон поглощения |
| 13 | __ __ A & (A v B) = A & B | __ __ A * (A +B) = A * B | |
| 14 | __ A v A & = A v B | __ A + A * B = A + B | |
| 15 | (A v B) v C = A v (B v C) (A & B) & C = A & (B & C) | (A + B) + C = A + (B + C) (A * B) * C = A * (B * C) | Правило ассоциативности |
| 16 | (A & B) v (A & C) = A & (B v C) (A v B) & (A v C) = A v (B & C) | (A*B) + (A*C) = A*(B+C) (A+B)*(A+C) = A+(B*C) | Правило дистрибутивности |
| 17 | A v A = A A & A = A | A + A = A A * A = A | Правило иденпотентности |
| 18 | A v B = B v A A & B = B & A | A + B = B + A A * B = B * A | Правило коммутативности |
| 19 | ____ __ __ A = B=A&BvA&B = (A+B)&(A+B) |
Пример:
________________
Упростите логическое выражение _____
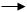 F = (A v B) (B v C)
F = (A v B) (B v C)
Это логическое выражение необходимо привести к нормальной форме, т.к. в нём присутствует импликация и отрицание логической операции.
1. Избавимся от импликации и отрицания.
Воспользуемся формулой (9). Получится:
_________________
______ ========
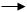 (A v B) (B v C) = (A v B) & (B v C))
(A v B) (B v C) = (A v B) & (B v C))
2. Применим закон двойного отрицания (4). Получим:
=======
(A v B) & (B v C) = (A v B) & (B v C)
3. Применим правило дистрибутивности (16). Получим:
(A v B) & (B v C) = (A v B) & B v (A v B) & C
4. Применим закон коммутативности (18) и дистрибутивности (16). Получим:
(A v B) & B v (A v B) & C = A & B v B & B v A & C v B v C
5. Применим (7). Получим:
A & B v B & B v A & C v B & C = A & B v B v A & C v B & C
6.Применим (16), т.е. вынесем за скобки В. Получим:
A & B v B v A & C v B & C = B &(A v 1) v A & C v B & C
7. Применим (6). Получим:
B &(A v 1) v A & C v B & C =B v A & C v B & C
8. Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:
B v A & C v B & C = B & (1 v C) v A & C
9. Применим (6). и получим ответ:
B & (1 v C) v A & C = B v A & C.
Ответ: F = B v A & C
Закрепление изученного материала:
Упростите выражения:
_____ _____
1. F = A & B v B v C;
2. 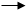
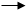 F = (A B) v (B A);
F = (A B) v (B A);
__
3. F = A & C v A & C;
Ответы:
_____ _____ __ _ _ __ __ __ _ _ _
1) F = A & B v B v C = A v B v B & C = B( 1v C) v A = A v B;
2) 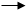
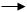 F = ((A B) v (B A) = A v B v B v A = (A v A) v (B v B) = 1 v 1 =1;
F = ((A B) v (B A) = A v B v B v A = (A v A) v (B v B) = 1 v 1 =1;
3) F = A & C v A & C = C &(A v A) = C;
Задание
Упростите логические выражения:
1) F = A v ( не A & B );
2) F = A & ( не A v B );
Дата: 2019-12-10, просмотров: 813.