Логика – как наука. История развития логики.
Высказывания в логике. Простые и сложные высказывания.
Логическая операция ИПЛИКАЦИЯ (от латинского implication – тесно связывать) – Логическое следование
 Обозначается так: А В,
Обозначается так: А В,
А – условие. В – следствие.
Если А, то В:
Таблица истинности
| А | В |  А В А В
|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Вывод: результат будет ложным тогда и только тогда, когда из истинного высказывания (А) следует ложное следствие (В)
Логическая операция ЭКВИВАЛЕНТНОСТЬ (от лат. Aequivalens – равноценное) – Логическое равенство.
 Обозначается так: А В
Обозначается так: А В
Таблица истинности
| А | В |   А В А В
|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Вывод: результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
В алгебре высказываний любую логическую функцию можно выразить через основные логические операции, записать её в виде логического выражения и упростить, применяя законы логики и свойства логических операций. По формуле логической функции легко рассчитать её таблицу истинности. Необходимо только учитывать порядок выполнения логических операций (приоритет) и скобки. Операции в логическом выражении выполняются слева направо с учетом скобок.
Приоритет логических операций:
СКОБКИ,
ИНВЕРСИЯ,
КОНЬЮНКЦИЯ,
ДИЗЬЮНКЦИЯ.
ИМПЛИКАЦИЯ
ЭКВИВАЛЕНТНОСТЬ
Вопросы:
1. Какие бывают высказывания? Привести примеры различных высказываний.
2. Дать понятие логическим переменным и логическим функциям. Придумать примеры.
3. Выучить таблицы истинности и привести примеры.
Использование логики высказывания в технике.
Задачи
3.1. Определите вид и число элементарных цепочек в электрических цепях.






















 А) Х У б) В a d
А) Х У б) В a d









 неХ c e
неХ c e




















 в) с d f г) a
в) с d f г) a










 a b b
a b b
c




 b d
b d



















 д) c x
д) c x
a неХ
Чтение электрических схем
Важно уметь читать электрические схемы, т.е. определять их состояние (есть ток или нет тока) в зависимости от состояния контактов при подключенном источнике тока.
 Упражнение 2. Дана схема: х
Упражнение 2. Дана схема: х










 z
z
У
Состояние контактов задаются таблицей, в которой используются введенные ранее обозначения: 0 – контакт разомкнут, 1 – контакт замкнут. Требуется заполнить колонку состояния схемы.
| х | у | z | Состояние схемы |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Решение. Первый случай (0; 1; 1). Замкнуты контакты У и Z, т.е. цепь для прохождения тока создана, состояние схемы –1. второй случай (1; 0; 1) аналогичен первому – ток будет проходить через замкнутые контакты Х и Z, состояние схемы –1. Третий случай (1; 1; 0), незамкнутый контакт Z создает обрыв в цепи, следовательно, ток проходить не будет, состояние схемы – 0.
Упражнение 3. В таблице задано состояние контактов схемы:








 B a c
B a c
 |  | ||||
 | |||||
неВ
| а | в | неВ | с | Состояние схемы |
| 1 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 |
Требуется заполнить последний столбец таблицы
Решение. Первый случай (1; 1; 0; 1). Цепочка замкнутых контактов А, В, С создает путь для тока, состояние схемы – 1. Второй случай (1; 0; 1; 1). Верхняя цепочка параллельного соединения разорвана, но цепь для тока создается через замкнутый контакт неВ, в цепи будет ток, состояние схемы – 1. Третий случай (1; 1; 0; 0). Независимо от состояния контактов А, В, при разомкнутых контактах С и неВ тока в цепи не будет, состояние схемы – 0.
Задачи
3.2. Представьте, себе что к приведенным ниже схемам подключили источник питания и прибор для измерения тока., состояние контактов задается таблицей, определите показания прибора (есть ток или нет).
А)
| А | В | С | D | ток |
| 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 0 |











 А В С
А В С
D 










Б)
| А | В | С | ток |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 1 | 1 |




 А
А


 В
В
 С
С
 |  |
| А | неА | В | С |  ток ток
|
| 1 | 0 | 1 | 0 |               
|
| 0 | 1 | 0 | 0 |   
|
| 1 | 0 | 1 | 1 |
В)
В
А
Не А
г)
| А | неА | В | С | D | ток |
| 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 1 |

























 А В
А В
D C
неА
Задачи
3.3. Составьте формулы логических функций к схемам:


 В неВ неВ
В неВ неВ



























 а) б) А В
а) б) А В

 А С неС
А С неС





























 В) А неD Г) а b c
В) А неD Г) а b c


 D f
D f



 Z
Z
F









 d) a b
d) a b



 c неC
c неC
 z
z




 x
x






















 ж) неУ
ж) неУ
неZ
У неХ
Вопросы:
1.Дать определение логическому элементу.
2. Параллельные и последовательные соединения. Таблицы истинности.
3. Научится читать электрические схемы.
4. научится составлять формулы логических функций.
Задача
1. Запишите логическую формулу, описывающую состояние схемы:
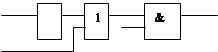 |
Х
 |
У
 Z
Z
2. Постройте схемы, работа которых описывается логическими формулами:
а) F(A,B,C) = (A и В) или (В и С);
б) F(Х,У) = (X или У) и неУ;
Задания
1. Запишите логическую формулу описывающую состояние схем:
а) б)

|
|

|
 А
А





 Х В
Х В








|

|

 Z D
Z D
2. Постройте схемы работа которых описывается логическими формулами.
а) F(A,B,C,F) = (A или В) и С и (В или F);
б) F(A,B,C,F) = (A или В) или (С и (В или F));
Задачи 1. В предложенных схемах запишите формулы выходных сигналов каждого логического элемента:
| ||||
 | ||||

















|
|
|
|
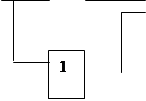 |  | ||||
 | |||||

 У
У
У
Z
|
|



|
|
 Х г) У
Х г) У












 в)
в)




У
Z
 Z
Z
|
|
|






 ж) Х
ж) Х

 У
У
 Z
Z
Задача 2. Постройте схему работа которой описывается логической формулой
F(A,B,C,D,F) = (C и D и А) или (В и F);
|
|
 Задачи 3. Запишите логическую формулу, описывающую состояние схемы, составьте таблицы истинности: Х
Задачи 3. Запишите логическую формулу, описывающую состояние схемы, составьте таблицы истинности: Х



|
|
 Х б)
Х б)












 А)
А)
 | ||
 | ||
 У У
У У
 Z Z
Z Z


|
|









|

|



 У
У
 У
У
 |  |
 Z
Z
Z











|
|
| |
Используя законы логики, упростите ее. Правильность преобразования проверьте таблицей истинности.


















 Задача 5. Два друга собрали схему. В результате тестирования (проверки выходного сигнала от всевозможных комбинаций входных) оказалось, что выходной сигнал D в точности повторяет один из трех входных. Укажите какой.
Задача 5. Два друга собрали схему. В результате тестирования (проверки выходного сигнала от всевозможных комбинаций входных) оказалось, что выходной сигнал D в точности повторяет один из трех входных. Укажите какой.
|


|
 B
B
 |


|

|

Составление логических схем по заданным таблицам.
Правило составления остается таким же, как при работе с контактными схемами.
Упражнение 1. По заданным таблицам истинности запишите функцию, составьте логические схемы.
а) б)
| а | в | F(а, в) |
| А | В | F(А,В) |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 |
Решение.
А) Берем строки, в которых F(A, B) = 1. Это вторая и третьи строки.
F(A,B) = (A и не В) или (не А и В)
Упростить формулу нельзя. Проверим правильность полученной формулы по таблице истинности, в которую записываются значения промежуточных сигналов.
| А | В | неА | неВ | А и неВ | неА и В | F(A, B) |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Значения F(A, B) в полученной и исходной таблицах совпадают при одних и тех же значениях входных сигналов, следовательно, формула верна. Строим схему:








|









|

|
 А неА неА и В
А неА неА и В
А и неВ
В неВ
Б) Для записи формулы выходной функции f(A,B) берем первую, вторую, четвертую строки таблицы, в которой F(A,B) = 1. F(A, B) =(А и В) или (неА и В) или (неА и неВ). Используя законы логики, упростим выражение: F(А,В) = (А и В) или (неА и (В или неВ) = (А и В) или неА и 1 = (А и в) или неА = (А или неА) и (В или неА) = 1 и (В или неА) В или неА. Формула выходной функции по заданной таблице F(А,В) = В или неА. Проверим её таблицей истинности:
| А | В | неА | F(А,В) |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 |
Полученная таблица совпадает с исходной по значениям входных сигналов А, В и соответствующим им выходных. Строим схему:



|
 А неА В или неА
А неА В или неА
 |
Задача 1.В комнате три выключателя - А, В, С:
А – при входе
В – над письменным столом;
С – над диваном.
Постройте схемы, которые позволяют включать свет следующим образом:
любым из следующих включателей
одновременно включением А и В или только С;
одновременно включением всех трех.


































 Задача 2. В формуле, описывающей схему, допущены ошибки, исправьте их, упростите схему:
Задача 2. В формуле, описывающей схему, допущены ошибки, исправьте их, упростите схему:
Х Z
У неХ
Z неZ
неУ
F(X,Y,Z) = ((X или У) или (Z или неХ)) и (У и (неZ и неУ)).
Задача 4 Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):
 |  |
 А В С А
А В С А







 1 0 0 В
1 0 0 В
 0 1 0 С
0 1 0 С

 1 1 1
1 1 1
Задание
а) б)
|
| ||||||||
 |  |  | |||||||
X
















|
 x ch
x ch
|
У Y


 Z Z
Z Z
в)
 | |||
|
X





 Y
Y
Задача 2. Судейская коллегия состоящая из трех членов, выносит решение большинством голосов при тайном голосовании. Постройте такую схему, чтобы голосование каждого члена «за» производилось нажатием кнопки (включением выключателя) и в случае принятия решения загоралась сигнальная лампа.
Задача 3. Представьте, что к приведенной схеме подключили источник питания и прибор для измерения тока, состояние контактов задается таблицей, определите показания прибора (есть ток или нет):



 А неА В С
А неА В С
1 0 1 0
0 1 0 0
1 0 1 1
Законы логики
Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной короткой и понятной форме.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания.
Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований.
Законы логики
| № п/п | Закон логики | Математическая запись | Название закона |
| 1 | А = А(А=А) | Закон тождества | |
| 2 | __ А & А = 0 | __ А * А = 0 | Закон непротиворечия |
| 3 | __ А v A = 1 | __ A + A = 1 | Закон исключающего третьего |
| 4 | == А = А | Закон двойного отрицания | |
| 5 | А & 0 = 0; A v 0 = A | А * 0 = 0; А + 1 = А | |
| 6 | A & 1 =A; A v 1 = 1 | A * 1 = A; A + 1 = 1 | |
| 7 | A & A = A; A v A =A | A * A =A; A + A =A | |
| 8 | __ A v A =1 | __ A + A =1 | Законы Моргана |
| 9 | ________ __
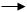 (A B) =A & B (A B) =A & B
| ||
| 10 | __
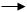 A B = A v B A B = A v B
| ||
| 11 | A & (A v B) = A | A * (A + B) = A | Закон поглощения |
| 12 | A v A & B =A | A + A * B =A | Закон поглощения |
| 13 | __ __ A & (A v B) = A & B | __ __ A * (A +B) = A * B | |
| 14 | __ A v A & = A v B | __ A + A * B = A + B | |
| 15 | (A v B) v C = A v (B v C) (A & B) & C = A & (B & C) | (A + B) + C = A + (B + C) (A * B) * C = A * (B * C) | Правило ассоциативности |
| 16 | (A & B) v (A & C) = A & (B v C) (A v B) & (A v C) = A v (B & C) | (A*B) + (A*C) = A*(B+C) (A+B)*(A+C) = A+(B*C) | Правило дистрибутивности |
| 17 | A v A = A A & A = A | A + A = A A * A = A | Правило иденпотентности |
| 18 | A v B = B v A A & B = B & A | A + B = B + A A * B = B * A | Правило коммутативности |
| 19 | ____ __ __ A = B=A&BvA&B = (A+B)&(A+B) |
Пример:
________________
Упростите логическое выражение _____
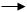 F = (A v B) (B v C)
F = (A v B) (B v C)
Это логическое выражение необходимо привести к нормальной форме, т.к. в нём присутствует импликация и отрицание логической операции.
1. Избавимся от импликации и отрицания.
Воспользуемся формулой (9). Получится:
_________________
______ ========
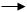 (A v B) (B v C) = (A v B) & (B v C))
(A v B) (B v C) = (A v B) & (B v C))
2. Применим закон двойного отрицания (4). Получим:
=======
(A v B) & (B v C) = (A v B) & (B v C)
3. Применим правило дистрибутивности (16). Получим:
(A v B) & (B v C) = (A v B) & B v (A v B) & C
4. Применим закон коммутативности (18) и дистрибутивности (16). Получим:
(A v B) & B v (A v B) & C = A & B v B & B v A & C v B v C
5. Применим (7). Получим:
A & B v B & B v A & C v B & C = A & B v B v A & C v B & C
6.Применим (16), т.е. вынесем за скобки В. Получим:
A & B v B v A & C v B & C = B &(A v 1) v A & C v B & C
7. Применим (6). Получим:
B &(A v 1) v A & C v B & C =B v A & C v B & C
8. Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:
B v A & C v B & C = B & (1 v C) v A & C
9. Применим (6). и получим ответ:
B & (1 v C) v A & C = B v A & C.
Ответ: F = B v A & C
Закрепление изученного материала:
Упростите выражения:
_____ _____
1. F = A & B v B v C;
2. 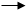
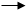 F = (A B) v (B A);
F = (A B) v (B A);
__
3. F = A & C v A & C;
Ответы:
_____ _____ __ _ _ __ __ __ _ _ _
1) F = A & B v B v C = A v B v B & C = B( 1v C) v A = A v B;
2) 
 F = ((A B) v (B A) = A v B v B v A = (A v A) v (B v B) = 1 v 1 =1;
F = ((A B) v (B A) = A v B v B v A = (A v A) v (B v B) = 1 v 1 =1;
3) F = A & C v A & C = C &(A v A) = C;
Задание
Упростите логические выражения:
1) F = A v ( не A & B );
2) F = A & ( не A v B );
Логика – как наука. История развития логики.
Дата: 2019-12-10, просмотров: 520.