Оборудование: Карточки с заданиями (класс разбивается на 3 группы и выбираются капитаны экипажей).
Ход урока
1. Организационный момент (проверяется наличие необходимого к уроку, наличие карточек).
2. Вступительное слово учителя о необходимости отправиться в путешествие по стране десятичных дробей), а всякое путешествие требует закалки, подготовки и тренировки. Проверим как мы к этому готовы.
а)Проверка домашнего задания, выполненного с преднамеренными ошибками: Заранее на лоске записывается учителем 1) (644,4+75,6):7,2=100; 3)(12,48-8,64):2,4=16 (1,6);
2) (3,9+13):1,3=1,3 (13) 4) (47-9,4): 4,7= 0,818
Необходимо пояснить ошибки.
б) Чтобы нас пропустили в эту страну, вы должны ответить на вопросы и выполнить устные задания (на магнитной доске на плакате изображены рисунки:
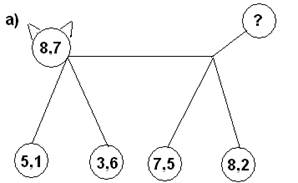 | 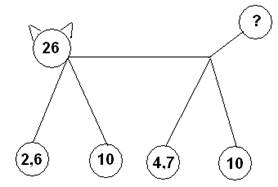 | ||

в) Дополнить каждое из чисел до 2,5 если числа даны : 1,5; 0,8; 1; 0,4 (команда, ответившая быстрее и верно, получает 1 очко).
3. Первый этап путешествия будет проходить на катере и чтобы оно прошло успешно, нужно решить задачу на определение скорости по течению и против течения ( Капитанам выдают карточки с заданиями а) Vm= 3,5 км/ч б) Vm = 3,7 км/ч
Vпр.т. =11,3 км/ч V по т = 15,7 км/ч
Vс- - ? V с - ?
V по т - ? V пр.т. - ?
в) Vпо т - 19,8 км/ч
Vc = 18 км/ч
Vm - ?
Vпр.т - ?
Пока капитаны решают задачи, все учащиеся должны приобрести билеты, а для этого выполнить задания (проверяются на обратной стороне доски)
Сравнить:
72,03 72,18 37,24 37,05
10,72 10,79 1,3 1,237
0,37 0,368 5,603 5,6
14,2 14,20 13,8 13,80
Решить уравнение
Х – 0 = 0,12 2,3 – Х = 1,5
7Х + 2,4 = 34,6 9Х + 3,9 = 31,8
Округлить до единиц (десятых)
13,87;403,524; 0,17; 38,52; 60,399; 0,52
(каждый ученик выполняет ее на месте)
4. Итак, все заняли свои места на катере, плывем против течения реки. Чтобы помочь катеру члены команд должны подбросить горючего, а для этого нужно каждому выполнить задание
(Проводится эстафета. Запись на доске).
1,4 + 1,6 = □ 3,6 + 0,4 = □ 2,8 + 1,2 = □
□ – 1,7 = □ □ – 2,4 = □ □ – 1,5 = □
□ • 1,3 = □ □ • 1,6 = □ □ • 2,5 = □
□ + 0,3 = □ □ + 0,44 = □ □ – 0,25= □
□ : 2 = □ □ : 3 = □ □ : 3 = □
□ – 0,2 = □ □ – 0,1 = □ □ – 0,4 = □
□ : 0,2 = □ □ : 0,2 = □ □ : 0,4 = □
5. Ребята, наш катер сел на мель, чтобы снять его с мели нужно решить задачу с комментированием.
а) В прямоугольнике одна из сторон равна 5,45 м, а вторая в 5 р больше. Найти площадь и периметр прямоугольника.
б) Второе задание размыло водой. Необходимо верно поставить запятую:
3 + 108 = 408 42 +7 = 112
63 – 27 =603 736 – 336 = 4
52 + 18 = 5
1. Дидактическая игра с числами (запятая перебегает с места на место, а ребята должны прочитать получившееся число). (Участвуют ребята, у которых на голове шапочка с цифрой).
2. Ребята, для завершения нашего путешествия вы должны выполнить самостоятельно задание. Найти значение буквенного выражения, записать ответ в строке «результат» и закрасить рисунок цветом, соответствующим данному результату.
(Каждый получает картинку)
1( а + в) х с : d
2 а х b : ( c + d)
3. Заключительное слово учителя:
Подведение итогов, оценки: Команда, набравшая 15 очков – 5, 10 очков – 4, меньше 10 очков – 3.
4. Стихотворение 0,3.
5. Д/з «Сочинить сказку о стране десятичных дробей».
Весь урок построен так, что ученики должны думать, анализировать, находить аналоги и делать соответствующие выводы. Кроме того идет работа в группах, где можно получить помощь товарища, что не запрещается, т.к. при этом идет более успешное осмысление материала. Групповая работа имеет место на многих уроках в различных вариантах: будь то пары постоянного или сменного состава или экипажи-группы. Групповая работа обязывает учащихся ответственно относиться к результатам учебного труда.
В работе с учащимися 9 класса уделяется большое внимание развитию речи учащихся. Учащиеся учатся описывать рисунок, т.е. рассказывать все, что они знают о фигуре, изображенной на рисунке. Большая роль уделяется теоретическим работам, которые способствуют более глубокому осмыслению изученного, а также лабораторным работам по геометрии.
Конспект урока по геометрии в 9 классе.
Тема урока: Прямоугольники (первый урок из обобщающего повторения за 9 кл).
Цели урока:
Обобщающие:
1) Повторить основные вопросы, связанные с понятием равнобедренного треугольника и его свойствами.
2) Вспомнить формулы для вычисления площадей треугольников.
3) Вспомнить соотношение между сторонами и углами треугольника.
4) Систематизировать знания учащихся по данной теме.
Развивающие: Способствовать развитию речи учащихся.
Учить учащихся обосновывать свои ответы.
Воспитывающие: Воспитание активного внимания;
Воспитание аккуратности при выполнении чертежей;
Формирование самостоятельности;
Развитие познавательной активности.
Тип урока: Обобщающе-повторительный.
Оборудование: Карточки с номерами 1, 2, 3
Карточки 2-х цветов с темной и светлой стороной;
Чертежи к задачам.
План урока:
1. Геометрическая перестрелка ( 5 мин.)
2. Описать рисунок (70 минут)
3. Задачи-картинки (80 минут)
4. Верно-неверно (13 минут)
5. Решение задач (20 минут)
6. Подведение итогов, задание на дом (2 м).
ХОД УРОКА:
1. Организационный момент
2. Повторение изученного и проверка домашнего задания.
а) Геометрическая перестрелка между учащимися 1 и 2 ряда. Проверка знаний основных определений и свойств.
Вопросы могут быть такими:
1. Какую геометрическую фигуру называют треугольником.
2. Какие треугольники называются равнобедренными.
3. Свойства равнобедренного треугольника.
4. Признак равнобедренного треугольника.
5. Какой треугольник называется прямоугольным.
6. Свойства прямоугольного треугольника.
7. Признаки равенства треугольников.
8. Медиана, биссектриса и высота треугольника.
9. Соответствие между сторонами и углами в треугольнике.
10. Равносторонний треугольник и его свойства.
б) Описать рисунок по чертежу (чертеж выполняется на пленке графпроектора).
Необходимо назвать как можно больше свойств фигуры, изображенной на рисунке)
(Можно назвать следующие свойства)
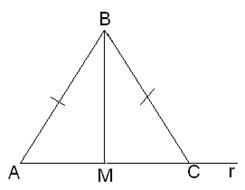 |
Рис.1.
1. Определение равнобедренного треугольника.
2. Теорема о свойстве углов равнобедренного треугольника.
3. Теорема о свойстве медианы равнобедренного треугольника, проведенной к основанию.
4. Теорема о свойстве внешнего угла треугольника
5. Теорема о сумме углов треугольника.
6. Определение внешнего угла.
7. Свойство биссектрисы угла.
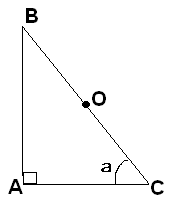
Рис. 2.
(Можно назвать следующие свойства
1. Определение прямоугольного треугольника, название его сторон.
2. Признаки равенства прямоугольных треугольников.
3. Свойства прямоугольного треугольника (их 2)
4. Определение sin, cos,tg.
5. Теорема Пифагора.
6. Решения прямоугольного треугольника.
7. Теорема о центре окружности, описанной около треугольника.
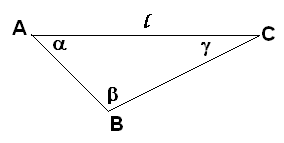
Рис.3.
Можно сформулировать следующие свойства:
1. Определение тупоугольного треугольника.
2. Соотношение между сторонами и углами треугольника.
3. Теорема Синусов.
4. Теорема Косинусов.
5. Неравенство треугольников.
В) Задачи на готовых чертежах с выбором ответов (Задачи-картинки).
Выбрать верный ответ доказать истинность
 |  | ||
1) 2)
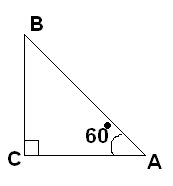
< DBA=20° AC=10
< DBA=55° АС=100см
 |
< DBA=35° АС=20см
 |
3)
г) Верно-неверно!(Задачи на доказательство)
1. Верно ли, что теорему Пифагора можно доказать из теоремы косинусов? (Доказать)
Верно ли, что в любом треугольнике либо все углы острые, либо 2 острых , а один прямой или тупой?
III Решить на закрепление
а) с взаимопроверкой и последующей проверкой ответов
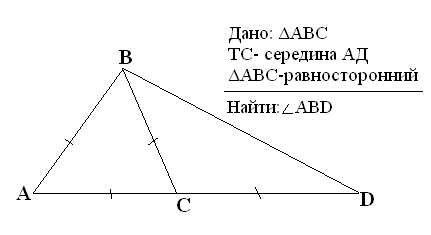
Решение:
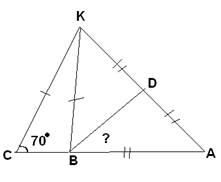
1) Так как Δ АВС - равносторонний,=> < А=<АВС=<АСВ=60°
2) Так как Δ СВD - равнобедренный,=> < СBD=<D
3) <BCA - внешний угол Δ, <CBD=<D=60°:2=30°; <ABD=<ABC+<CBD=60°+30°=90°
б) На доске:
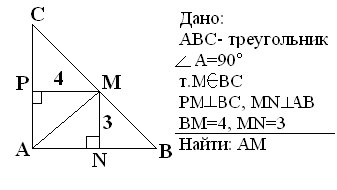
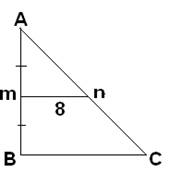
Решение: так как РМ ┴ АС, МN ┴ AB и АС ┴ АВ => PMNA- прямоугольник, АМ- диагональ, ∆AMN- прямоугольный, найдем АМ по теореме, обратной теореме Пифагора: AN² + NM²=5(см).
В работе с учащимися 10-11 классов я использую лекционно-семинарскую систему. Урок-лекция, как правило, позволяет дать материал крупными блоками. Поэтому эта система нашла свое применение при изучении тем: «Прогрессия, уравнения и неравенства», «Способы преобразования многочленов, логарифмическая, показательная функция, тригонометрические функции, тригонометрические уравнения и неравенства и др.
Дата: 2019-12-10, просмотров: 345.