R,t диаграмма движения вещества в камере реактора приведена на Рис. 14. Как показал расчет, процесс разлета мишени (фаербола) и испарения защитной пленки первой стенки завершается столкновением двух фронтов примерно через 12 мкс после микровзрыва.

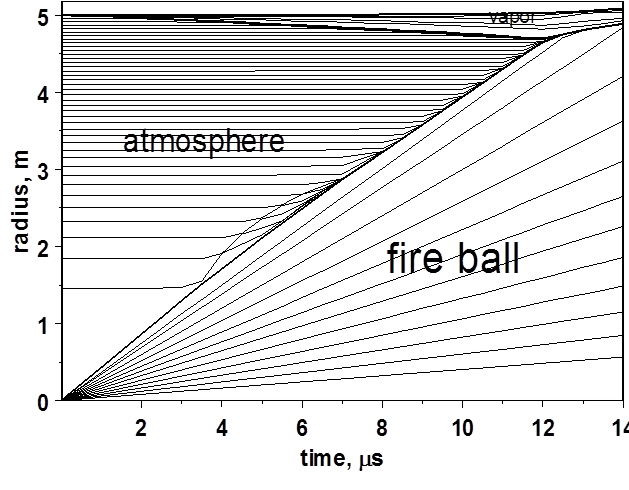
Рис. 14. R,t диаграмма движения вещества в камере реактора.

Диаграмма Рис. 14 предсталяет результат совместного расчета процессов разлета мишени, распространения ударной волны по атмосфере камеры и испарения внутрь камеры защитной жидкой пленки первой стенки. Видно, что столкновение двух встречных фронтов – фаербола и ионизованного пара – происходит приблизительно через 12 мкс после взрыва мишени на расстоянии около 40 см от стенки. После столкновения паровой слой нагревается до 10⁶ К, что вызывает доиспарение защитной пленки. Ионизованный пар теплоносителя продолжает расширяться внутрь камеры. Масса испаренного вещества перед столкновением двух фронтов составляет 1,5 кг. После доиспарения в камере единовременно находится около 10 кг испаренного вещества.

Распределение скорости в фаерболе практически линейное, его граница движется с почти постоянной скоростью порядка 400 км/с. В результате по атмосфере камеры распространяется ударная волна (Рис. 15). Поскольку масса атмосферы существенно меньше массы фаербола, траектории частиц атмосферы практически сливаются с линией фронта скачка давления.

Радиальные распределения давления, скорости течения и плотности среды (фаербола, атмосферы камеры, пара), в различные моменты времени показаны на Рис. 15-17.

На Рис. 18-20 показано радиальное распределение температуры в фаерболе, атмосфере камеры и в испаренном слое защитной пленки в различные моменты времени.

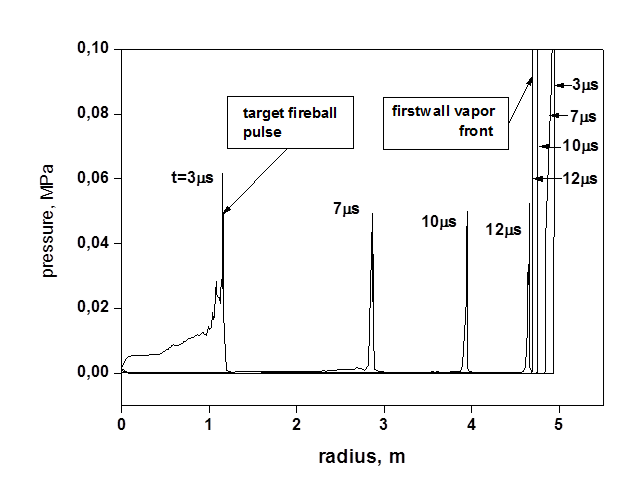
Рис. 15. Распределение давления в фаерболе, атмосфере камеры и паре

График Рис. 15 показывает встречное движение двух ударных волн. Слева направо по атмосфере камеры распространяется импульс давления от фаербола. Положение импульса показано через 3 мкс, 7 мкс, 10 мкс и 12 мкс (последнее – перед моментом столкновения фронтов). Эта ударная волна имеет высокую скорость движения (400 км/с, см. ниже Рис. 16), но вследствие интенсивного расширения вещества давление на фронте невелико – около 50 кПа (0,5 бар).

Справа налево движется фронт испаренного вещества. Скорость его движения 30 км/с примерно на порядок ниже скорости движения фронта фаербола, но плотность вещества в ионизованном паре высокая. В результате давление в паре на два порядка превосходит давление в фаерболе и составляет перед столкновением 5 МПа. На Рис. 15 для удобства восприятия линии фронтов давления в паровом слое «обрезаны» в их верхней части.

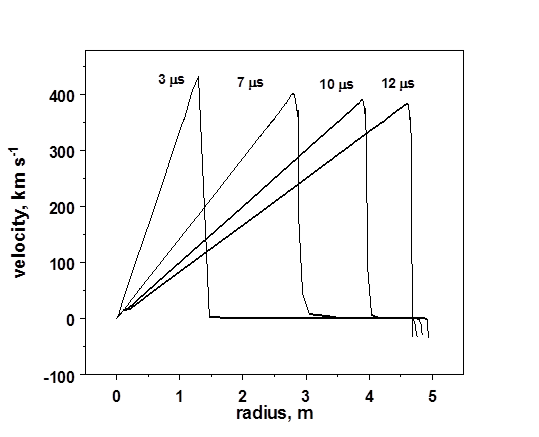
Рис. 16. Радиальное распределение скорости вещества в фаерболе и атмосфере.

Радиальные распределения скорости и плотности вещества фаербола в различные моменты времени представлены на графиках Рис. 16 и 17. Распределение скорости в файерболе практически линейно. Вещество атмосферы ускоряется в ударных волнах, возникающих в результате расширения фаербола и испаряющейся пленки. Максимальная плотность в импульсе, распространяющемся от центра камеры, падает от 10⁵ кг/м³ в момент выхода ударной волны на поверхность мишени до 10^-4 кг/м³ в момент столкновения встречных ударных волн вблизи стенки камеры.

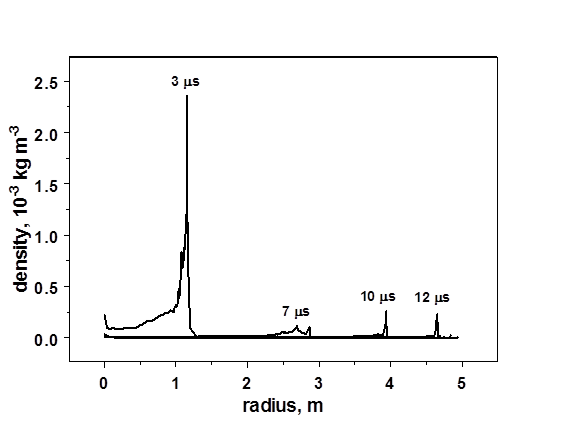
Рис. 17. Распределение плотности вещества в фаерболе и атмосфере

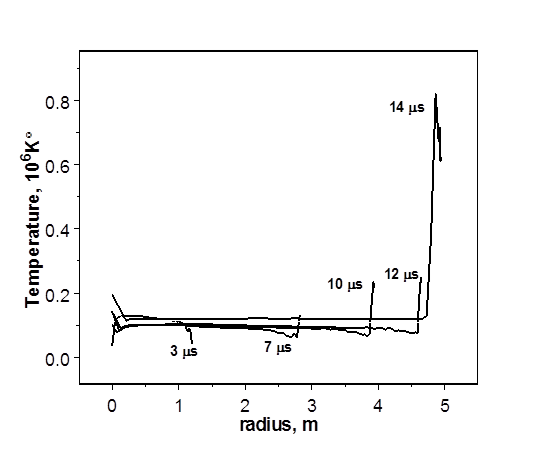
Рис. 18. Распределение температуры в фаерболе

Графики распределения температуры в системе «фаербол-атмосфера-пар» показывают, что динамика изменения температуры в указанных составляющих различна. Фаербол (Рис. 18) при разлете расширяется и равномерно остывает. Некоторый рост температуры в последней расчетной ячейке фаербола, граничащей с атмосферой камеры, обусловлен сжатием в ней вещества и высоким давлением; эта ячейка отвечает положению фронта ударной волны, распространяющейся по атмосфере камеры.

Атмосфера (Рис. 19), в свою очередь, прогревается излучением, выходящим из фаербола и из примыкающих к нему слоев, которые сжимаются и имеют высокую температуру. Наблюдается отрыв температуры от фронта ударной волны за счет эффектов лучистой и электронной теплопроводности (см. [16, стр. 401, 410]). На прогрев области атмосферы перед фронтом ударной волны указывают характерные «брюшки» спадающих профилей температуры.

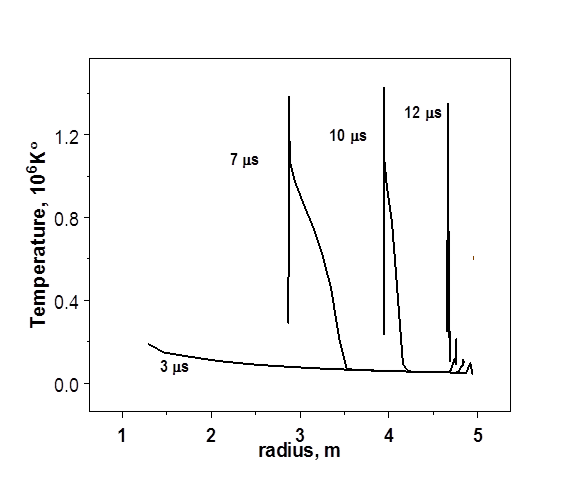
Рис. 19. Распределение температуры в атмосфере камеры

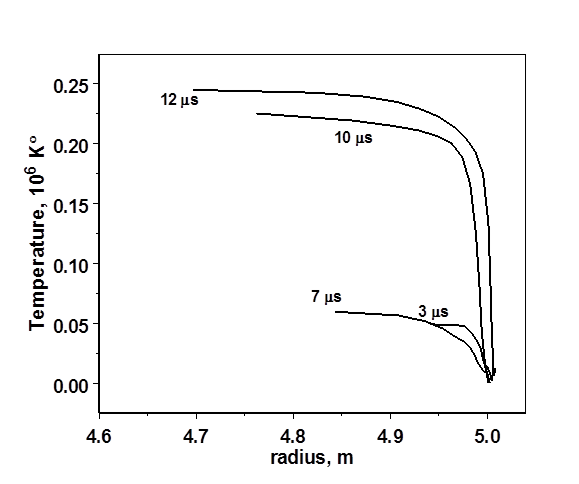
Рис. 20. Распределение температуры в испаренном слое жидкой пленки в различные моменты времени

Испаренный слой защитной жидкой пленки расширяется внутрь камеры, одновременно нагреваясь излучением, идущим из фаербола. На Рис. 20 видно, что с ростом времени «хвосты» ионизованного пара удаляются от первой стенки, одновременно с этим нагреваясь.

После столкновения двух фронтов температура и давление в соответствующей расчетной ячейке камеры резко возрастают. Важно, однако, что процесс релаксации, стимулированный доиспарением вещества жидкой пленки, приводит к весьма быстрому снижению температуры в этой ячейке в течение первых трех микросекунд после столкновения – примерно с темпом 100 тысяч градусов за микросекунду или 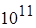 К/с. В результате температура и давление в зоне столкновения снижаются, движение вещества к стенке камеры прекращается и начинается его равномерное размешивание по объему камеры.

Модель последующей релаксации атмосферы камеры была рассмотрена в работах [4-6]. В них было показано, что в течение приблизительно 0,02 с температура и плотность вещества в камере приходят к равновесному состоянию до взрыва.

Заключение

Моделирование полного сценария микровзрыва мишени и отклика камеры реактора на микровзрыв требует создания, по меньшей мере, двух различных гидродинамических кодов – одного для описания сжатия мишени, ее поджига и горения, и второго для описания разлета мишени, абляции первой стенки и взаимодействия встречных потоков вещества в камере. Это обусловлено принципиальным отличием физики процессов, протекающих на этих двух этапах, а также громадным отличием в них характерных масштабов времени, размеров, гидродинамических параметров и плотностей потоков массы импульса и энергии.

В данной работе моделирование микровзрыва мишени выполнено посредством последней версии кода DEIRA-4, а моделирование разлета мишени и отклика камеры реактора – с помощью вновь созданного кода радиационной гидродинамики. Сконструирована процедура сопряжения решений двух кодов с различной геометрией течения.

На основе кода DEIRA-4 осуществлен подбор энергетически эффективной мишени и режимных параметров тяжелоионных пучков, обеспечивающих требуемый уровень генерации термоядерной энергии в концепции ИТИС. Полностью определены временные профили потоков энергии, переносимых нейтронами, заряженными частицами и излучением в процессе микровзрыва, а также поля гидродинамических переменных в момент выхода ударной волны на свободную поверхность мишени.

В данной работе представлена модель и результаты численного сопряженного расчета разлета мишени в камере и воздействия продуктов термоядерного микровзрыва на первую стенку камеры реактора. Важность этой части работы заключается в том, что в ней впервые проведены численные расчеты отклика камеры реактора на микровзрыв в рамках одной программной реализации, позволяющей решать систему уравнений гидродинамики и переноса излучения не только для аномально высоких плотностей энергии (как непосредственно в фаерболе), но и для экстремальных условий (абляция жидкой пленки), а также в разреженной атмосфере камеры.

Благодарности

Авторы отмечают решающее влияние на эту работу академика В.И. Субботину, инициировавшему в Научном Совете РАН по физико-техническому анализу энергетических систем разработку концепции ИТИС. Авторы также глубоко благодарны члену-корреспонденту А.В. Забродину, руководившему работами по концепции ИТИС в ИПМ РАН, за поддержку и постоянное внимание к проводимым исследованиям.

Мы выражаем признательность академику В.П. Смирнову и члену-корреспонденту Б.Ю. Шаркову за многочисленные плодотворные обсуждения затрагиваемых вопросов. Мы также благодарим докторов физико-математических наук М.В. Масленникова и С.Л. Недосеева за критические замечания, полезные советы и ценные замечания по работе в ходе дискуссий на научных семинарах по проблемам ИТС.

Особую благодарность авторы выражают доктору физико-математических наук В.Г. Новикову за проведение расчетов коэффициента поглощения излучения в плазме свинца и релаксационного члена в однотемпературном приближении.

Литература

1. Medin S.A., Churazov M.D., Koshkarev D.G. et al. Evaluation of a power plant concept for fast ignition heavy ion fusion // Laser and Particle Beams, 2002. V.20, p.419–423.

2. Basko M. M., Churazov M. D., Aksenov A. G. Prospects of heavy ion fusion in cylindrical geometry. // Laser and Particle Beams, 2002. V.20, p.411–414.

3. Medin S.A., Churazov M.D., Koshkarev D.G., et al. Reactor Chamber and Balance-of-Plant Characteristics for Fast-Ignition Heavy-Ion Fusion Power Plant // Fusion Science and Technology, 2003. V.43, No.3, p.437–446.

4. Медин С.А., Орлов Ю.Н., Суслин В.М., Паршиков А.Н. Моделирование отклика первой стенки камеры и бланкета реактора ИТС на микровзрыв. / Препринт ИПМ им. М.В. Келдыша РАН, № 41, 2004.

5. Медин С.А., Орлов Ю.Н. Концепция камеры реактора ИТС на тяжелых ионах // ВАНТ, сер. Термоядерный синтез, 2005. Вып. 2. С. 3-14.

6. Medin S.A., Basko M.M., Koshkarev D.G., Orlov Yu.N., Parshikov A.N., Sharkov B.Yu., Suslin V.M. Power Plant Design and Accelerator Technology for Heavy Ion Inertial Fusion Energy // Nuclear Fusion, 2005. V. 45. S291-S297.

7. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, 1993. Vol.106 A, No.11, p.1567–1571.

8. Кошкарев Д.Г., Чуразов М.Д., Баско М.М. и др. Мощный тяжелоионный драйвер для зажигания термоядерной ДТ мишени. / Препринт ИТЭФ, 4-01, 2001.

9. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, 2001. Вып. 1, №.20, с.1–13.

10. Долголева Г.В., Забродин А.В. Кумуляция энергии в слоистых системах и реализация безударного сжатия. М.: Физматлит, 2004, 70 с.

11. Basko M.M. DEIRA 1D-3T hydrodynamic code for simulating ICF targets driven by fast ion beams. / Moscow: ITEP, 2001.

12. Медведев А.Б. Модификация модели Ван-дер-Ваальса для плотных состояний. / В сб.: Ударные волны и экстремальные состояния вещества. Под ред. В.Е. Фортова, Л.В. Альтшулера, Р.Ф. Трунина и А.И. Фунтикова. М.: Наука, 2000.

13. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971.

14. Никифоров А.Ф., Новиков В.Г., Уваров В.Б. Квантово-статистические модели высокотемпературной плазмы и методы расчета росселандовых пробегов и уравнений состояния. М.: Физматлит, 2000.

15. Hubbell J.H., Seltzer S.M. Tables of X-Ray Mass Attenuation Coefficients. NIST, 1996.

16. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966.

17. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика VI. Гидродинамика. М.: Наука, 1988.

18. dai Kai Sze, Ralph Moir, Steve Zinkle. Data Base for Liquid Breeders and Coolants. / APEX Interim Report, November, 1999.

19. Драгалов В.В., Никифоров А.Ф., Новиков В.Г., Уваров В.Б., Статистический метод расчета поглощения фотонов в плотной высокотемпературной плазме, Физика плазмы, 1990, т.16, № 1, с.77-85.

20. Новиков В.Г., Никифоров А.Ф., Уваров В.Б., Драгалов В.В. Поглощение фотонов в высокотемпературной плазме. / Препринт ИПМ им. М.В. Келдыша РАН, № 17, 1992. – 22 с.

21. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1980.

22. Медин С.А., Орлов Ю.Н., Суслин В.М. Расчет динамики испарения защитной пленки первой стенки камеры реактора ИТС / Препринт ИПМ им. М.В. Келдыша РАН, № 62, 2004. – 28 с.

23. S.A. Medin, M.M. Basko, Yu.N. Orlov and V.M. Suslin. X-ray and Ion Debris Impact on the First Wetted Wall of IFE Reactor. / 33-d European Physical Society Conference on Plasma Physics. Roma, Italy, June 19-23, 2006. Collected abstracts, p.32.