При расчете динамики испарения защитной пленки под воздействием излучений, идущих из мишени, следует опираться на сценарий последовательности воздействий продуктов микровзрыва на стенку камеры. Важно учитывать, что продукты реакции достигают первой стенки за различное время.

Согласно результатам расчетов горения мишени, полученных по программе DEIRA-4 [11] в параграфе 3, первая стенка камеры реактора последовательно подвергается импульсным воздействиям различной физической природы и мощности.

Первым воздействием на жидкую пленку является короткий (0,5 нс) и мощный (240 ТВт) пред-импульс рентгеновского излучения, образующийся при выходе ударной волны на поверхность мишени (это происходит примерно через 9 нс после начала DT-реакции, см. Рис. 9 и 10). Через 13 нс после излучения пред-импульса с поверхности мишени он достигает первой стенки камеры, что происходит, таким образом, через 22 нс после микровзрыва. Следом за пред-импульсом через 77 нс после микровзрыва на стенку приходит поток нейтронов 14 МэВ, длительность которого равна времени эффективного горения мишени и составляет примерно 0,1 нс. Поток нейтронов 2,5 МэВ от DD-реакции приходит на стенку камеры через 182 нс после микровзрыва, но их доля в нагреве теплоносителя сравнительно мала, поэтому далее этим вкладом пренебрегаем. Основной рентгеновский импульс начинает воздействовать на жидкую пленку через 220 нс после микровзрыва.

Наибольший вклад в энерговыделение при горении DT-топлива вносят нейтроны с энергией 14 МэВ, для которых мишень практически прозрачна. Нагрев жидкой пленки нейтронами невелик вследствие большого пробега в свинце ~16см. Рентгеновское излучение, выходящее впоследствии с поверхности мишени, характеризуется планковским спектром, дилютированным за счет радиального распространения от взорвавшейся мишени. Собственно энергия, заключенная в мишени, определяется главным образом энергией альфа-частиц, возникших в ходе DT-реакции. Разлет мишени описывается системой уравнений гидродинамики с учетом энергии излучения. Это система уравнений двухтемпературной гидродинамики – с температурой вещества 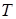 и температурой излучения .

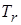Мишень на стадии разлета предполагается сферической и состоящей из свинца, для которого используется широкодиапазонное уравнение состояния А.Б. Медведева [12]. В камере в начальный момент времени находится пар теплоносителя с температурой первой стенки 823 K, создавая давление 0,01 Па. Начальным моментом для задачи о разлете является момент выхода ударной волны на поверхность мишени, которому отвечает момент времени 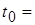104,3 нс (см. Рис. 5-8).

Отклик первой стенки камеры на микровзрыв определяется разогревом защитной пленки проходящим потоком нейтронов и ее абляцией под воздействием теплового излучения разлетающейся мишени.

При описании теплопроводности в жидкой пленке учитывается также электронная теплопроводность, согласно [13]. Для упрощения модели переноса тепла за счет нейтралов и электронов в работе применяется взвешенный коэффициент теплопроводности с весами, пропорциональными плотностям соответствующих компонент.

В разлетающейся мишени перенос теплового излучения описывается в диффузионном приближении с использованием данных [14] о росселандовых пробегах в плазме свинца с заданной температурой и плотностью.

Перенос рентгеновского излучения в атмосфере камеры моделируется на основе расчетных данных о его мощности и температуре на поверхности мишени, представленных на Рис. 10. Эти данные «переносятся» на первую стенку камеры с учетом дилютирования излучения в сферической геометрии и частичным его поглощением в атмосфере камеры. Для этого в уравнение энергии вещества вводится дополнительный источниковый член, определяющий плотность мощности поглощения излучения. Расчет глубины поглощения рентгеновского излучения в свинце основывается на спектральных данных лаборатории NIST [15].

Камера для простоты моделирования считается сферической. На границе жидкой пленки с первой стенкой камеры поддерживаются равновесные параметры. Считается также, что в начальный момент возмущения в атмосфере камеры и в защитной жидкой пленке отсутствуют, а все теплофизические параметры в пленке отвечают равновесному состоянию.

Таким образом, в данном разделе работы мишень в процессе своего разлета, атмосфера камеры и защитная пленка первой стенки описываются сквозным образом одной и той же системой уравнений. Это является новым шагом по сравнению с работами [4, 5].

Разлет мишени и перенос излучения в камере рассчитываются по самостоятельной программе, отличной от описанной выше модели DEIRA-4, которая поставляет данные начальных условий для задачи разлета. Мишень в гидродинамических расчетах считается сферической, как и камера, в которой происходит микровзрыв. Эти упрощения не принципиальны, поскольку характерный размер мишени (1 см) много меньше размера камеры (5 м), а излучение нейтронов и рентгеновских лучей можно считать изотропным.

Выпишем систему уравнений, описывающих поведение вещества в камере после микровзрыва. Они аналогичны системе уравнений (2.6)-(2.14), но отличаются от нее более упрощенной структурой. В этой системе, в частности, все вещество имеет одну температуру, так что электронные и ионные температуры совпадают.

Уравнения гидродинамики

Для описания процессов разлета мишени в камере и испарения защитной пленки первой стенки законы сохранения массы, импульса и энергии имеют вид [16, 17]

,      

,

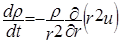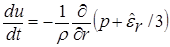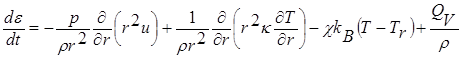,                    (4.1)

,

.

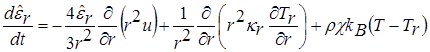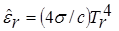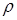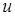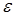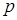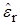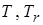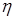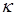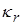Здесь  – плотность,  – скорость,  – удельная внутренняя энергия вещества [Дж/кг],  – давление,  – плотность энергии излучения [Дж/м³],  – температуры соответственно вещества и излучения,  – коэффициент вязкости,  и  – коэффициенты теплопроводности,  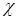– коэффициент температурной релаксации излучения и вещества,  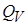– плотность энергии поглощения излучения в свинце. Обозначения универсальных постоянных:  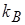– постоянная Больцмана,  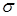– постоянная Стефана-Больцмана,  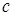– скорость света в вакууме.

4.3. Коэффициенты вязкости и теплопроводности

Коэффициент вязкости свинца в диапазоне 500-1000 К определяется по эмпирической зависимости [18]:

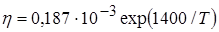.                                                                           (4.2)

При 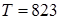 К его значение равно 0,001 Па∙с. В отсутствие достоверных опытных данных при больших температурах вязкость положена равной нулю.

Коэффициент теплопроводности в веществе представляется в виде взвешенной суммы электронной и нейтральной компонент

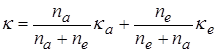,                                                                           (4.3)

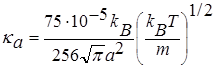, a = 1,8∙10^-10 [м],

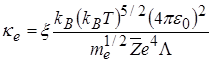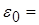,  8,85∙10^-12 [СИ],

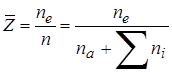, i=1,2,…,82,

где суммирование ведется по зарядовым состояниям иона свинца 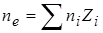, а параметр  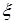слабо зависит от  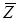(например, 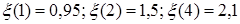). Кулоновский логарифм вычисляется по формул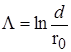е , где

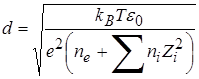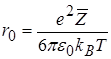, .                                                   (4.4)

Коэффициент радиационной теплопроводности определяется по формуле [13]:

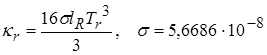 [СИ].                                                       (4.5)

Здесь 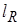 есть средняя длина пробега по Росселанду:

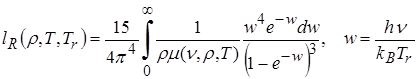,                                (4.6)

где 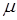 – массовый коэффициент поглощения излучения в среде [см²/г], так что величина  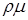имеет размерность обратной длины.

4.4. Коэффициенты поглощения и температурной релаксации

Релаксация между температурой электронов и температурой излучения описывается коэффициентом 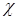 в правой части (4.1). Этот коэффициент определяется в [11] по формуле

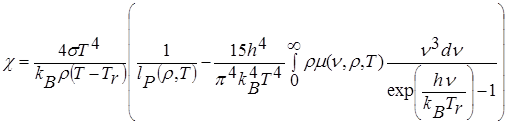,            (4.7)

где средний планковский пробег 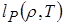 определяется интегралом

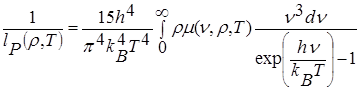.                                            (4.8)

Таким образом,

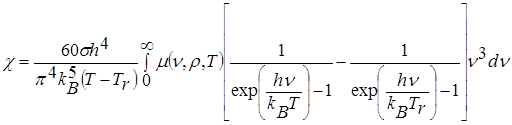.           (4.9)

Формула (4.9) определяет 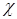 как функцию плотности и двух температур – вещества и излучения. Однако двухтемпературная зависимость сильно усложняет процесс расчетов, поскольку для их проведения требуется табуляция  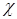путем численного интегрирования функционала (4.9) от эмпирической величины массового поглощения 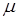. Будучи разложена в ряд по степеням 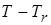, формула (4.9) в первом приближении дает независимость  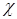от температуры излучения:

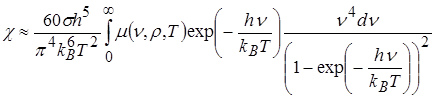.                          (4.10)

Таким образом, коэффициент релаксации приближенно можно записать в виде, аналогичном коэффициенту радиационной теплопроводности (4.5):

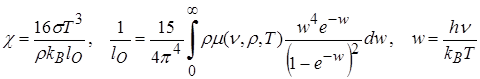.                 (4.11)

Нахождение величин 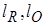 связано с вычислением интегралов (4.6), (4.11), в которых спектральный коэффициент поглощения фотонов  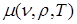в широкой области температур и плотностей для плазмы свинца был определен расчетным путем на основе программы THERMOS [14]. Указанные расчеты были проведены на основе релятивистской самосогласованной модели Хартри-Фока-Слэтера. В этой модели уровни энергий ионов и положения спектральных линий вычисляются в одноконфигурационном приближении Хартри-Фока. Вероятности различных состояний ионов определяются с использованием распределения Гиббса. В качестве профиля линий используется профиль Фойгта с учетом естественного уширения, уширения электронами, эффекта Штарка и эффекта Доплера, а также эффектов спин-орбитального расщепления методом Мошковского [19]. Расчет сечений фотоионизации проводится с использованием численных волновых функций электронов дискретного и непрерывного спектра, вычисленных в самосогласованном потенциале. При вычислении сечения тормозного поглощения используется модифицированная формула Борна-Эльверта с учетом эффектов вырождения. Комптоновское рассеяние вычисляется по уточненной формуле Клейна-Нишины.

Верификация программы THERMOS была проведена путем сопоставления с результатами расчетов по программам ведущих зарубежных центров – Ливерморской национальной лаборатории США (программы OPAL и HOPE), Лос-Аламосской национальной лаборатории США (программа LEDCOP), лаборатории Бер Шева из Израиля (программа STA). Проведены также сравнения с известными экспериментальными данными по измерению коэффициента прохождения (трансмиссии) для плазмы алюминия, железа, германия и гольмия [20]. Показано, что точность программы THERMOS при расчете детальных спектров достаточно высока. При расчете как детальных спектров, так и средних характеристик (в частности, усредненных по Плакнку и по Росселанду коэффициентов поглощения), получено хорошее согласие с наиболее продвинутыми зарубежными программами.

Пример расчетного коэффициента поглощения для плазмы свинца приведен на Рис. 11. Расчет проведен для температуры T=250 эВ и плотности ρ=10^-2 г/см³. Весовая функция Планка соответствует штриховой линии, а весовая функция для вычисления величины 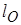 обозначена пунктирной линией. Как видно из Рис. 11, использование весовой функции (4.11) смещает область влияния спектра поглощения в сторону больших энергий фотонов по сравнению с планковской весовой функцией (4.8).

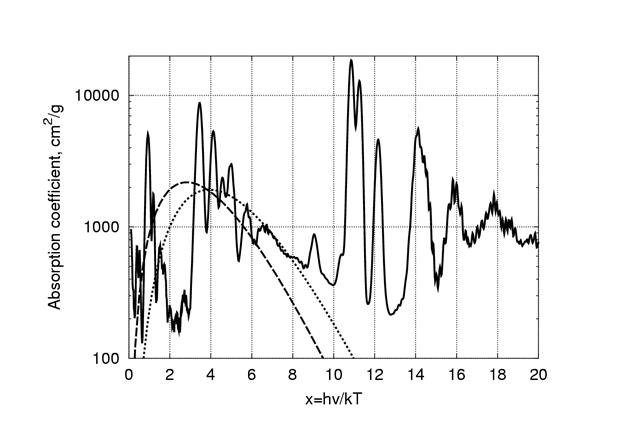
Рис. 11. Коэффициент поглощения в плазме свинца 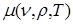при температуре T = 250 эВ и плотности ρ = 10^-2 г/см³ (сплошная линия)

Усредненные с помощью весовой функции (4.11) величины 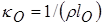 в широкой области температур и плотностей представлены ниже на Рис. 12. Для удобства визуализации на графике представлены величины 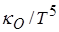. Характерная скейлинговая зависимость коэффициента  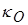от температуры и плотности среды в рассматриваемом диапазоне параметров приближенно может быть описана формулой  ~ .

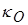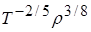Источниковый член в уравнении энергии (4.1) имеет вид 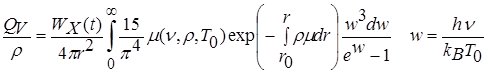.               (4.12)

Здесь индексом 0 отмечены значения переменных на контактной поверхности между мишенью и атмосферой камеры. Контактная поверхность движется по траектории r₀(t). Значения параметров W_X(t) и Т₀(t) берутся из расчетов по программе DEIRA-4 (см. графики на Рис. 10).

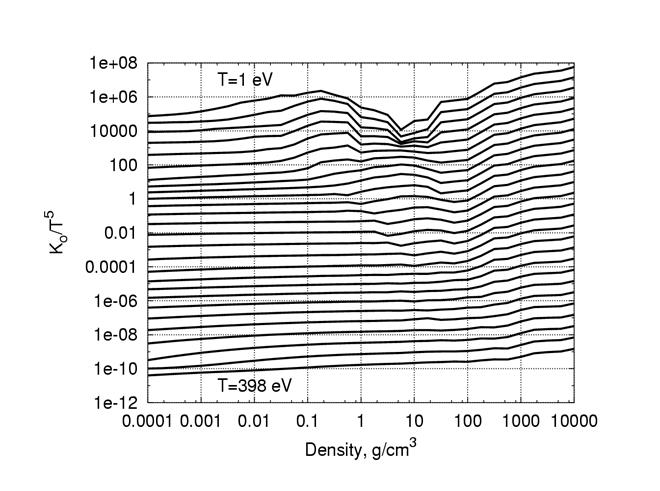
Рис. 12. Изотермы коэффициента 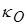 в плазме свинца. Изотермы приведены с равномерным шагом по логарифму Т от 1 эВ до 398 эВ

Уравнение состояния

Широкодиапазонное уравнение состояния А.Б. Медведева [12] определяет зависимость 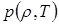 неявным образом через подгоночный параметр – т.н. «объем коволюма» 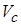. Само давление представляется в виде двух слагаемых – давления отталкивания  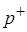и давления притяжения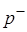

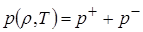                                           ,                                         (4.13)

зависящих от 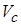. Ведем безразмерные величины 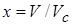, , 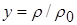где 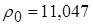г/см³ – некоторая постоянная, имеющая размерность плотности, своя для каждого вещества (в данном случае – для свинца). В модели [12] для свинца предложены следующие зависимости для определения  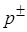[ГПа]:

- во всей области давлений ;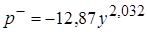

- при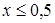  

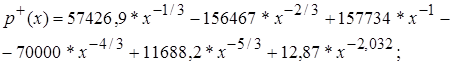
- в диапазоне 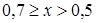 применяется формула

;

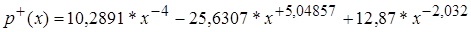- при .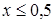

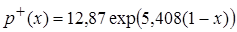Уравнение, которым определяется 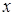, а, следовательно, по формулам, определенным выше, и давление 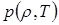, имеет вид:

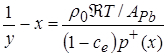.                                                                                    (4.14)

Здесь 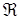 – газовая постоянная, а 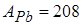– молярная масса свинца.

Система уравнений (4.13-4.14) показывает, что давление в модели в отсутствие ионизации определяется как функция температуры и плотности. По заданным значениям 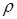 и 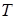 из неявной зависимости (4.14) численно определяется значение виртуальной переменной 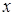, после чего по формуле (4.13) находится давление .

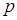С учетом ионизации в модель добавляется расчет концентрации ионов i-кратной ионизации 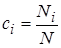, который проводится в предположении равновесия по формуле Саха:

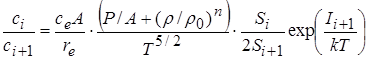,                                        (4.15)

где 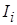 – соответствующий потенциал ионизации свинца [13], 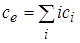,  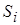– т.н. внутренняя статистическая сумма (в расчетах полагаем ), .

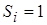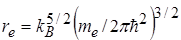Термическое уравнение состояния включает в себя энергию взаимодействия между частицами неидеальной среды, тепловую энергию и энергию ионизации:

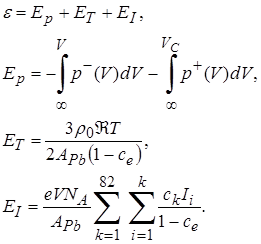                                                                (4.16)