Содержание
1. Введение ……………………………………………………………………...4
1.1. Концепция тяжелоионного DT-синтеза с быстрым поджигом ………....4
1.2. Базовые пераметры ЯЭУ на основе тяжелоионного DT-синтеза …….…5
2. Физико-математическая модель сжатия и горения мишени …....................7
2.1. Взамодействие тяжелоионного пучка с оболочкой мишени ………….…7
2.2. Уравнения сохранения трехтемпературной гидродинамической
модели ……………………………………………………………………….8
2.3. Уравнения диффузии заряженных частиц и кинетики
термоядерного горения …………………………………………….……...10
3. Результаты расчетов сжатия и горения мишени …………………………...11
3.1. Динамика сжатия мишени цилиндрическим пучком ……………………11
3.2. Выход ударной волны на поверхность мишени, генерация
импульсов энергии нейтронов и рентгеновского излучения …………...13
4. Физико-математическая модель разлета мишени и испарения
защитной жидкой пленки первой стенки камеры …………………………….16
4.1. Сценарий разлета мишени и испарения защитной пленки .…………......16
4.2. Уравнения гидродинамики ………………………………………………...18
4.3. Коэффициенты вязкости и теплопроводности ……………………………19
4.4. Коэффициенты поглощения и температурной релаксации ………………20
4.5. Уравнение состояния ………………………………………………………..23
4.6. Начальные и граничные условия для расчета разлета мишени
и абляции жидкой пленки …………………………………………………..24
4.7. Алгоритм расчета и численная схема ……………………………………...25
5. Результаты расчетов разлета мишени и абляции жидкой пленки ….............26
5.1. Отклик жидкой пленки на воздействие рентгеновского
пред-импульса и нейтронного потока ……………………………………...26
5.2. Разлет облака мишени и абляция жидкой пленки …………………………27
6. Заключение …………………………………………………………………….34
Благодарности ……………………………………………………………………34
Литература………………………………………………………………………...35
ВВЕДЕНИЕ
Физико-м атематическая модель сжатия и горения мишени
Уравнения диффузии заряженных частиц и кинетики термоядерного горения
Диффузионные уравнения для плотности энергии заряженных частиц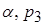 
и 
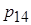записываются в нижеследующем виде (в левых частях уравнений стоят полные, т.е. лагранжевы, производные по времени):
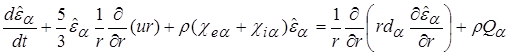, (2.12)
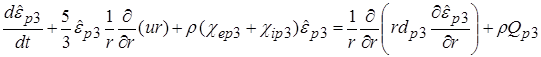, (2.13)
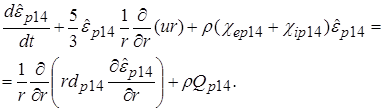(2.14)
Коэффициенты диффузии заряженных продуктов синтеза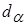 
, 
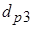и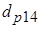 
выражаются через начальную энергию и суммарный коэффициент релаксации энергии соответствующих частиц. Источники 
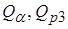и 
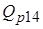определяются с помощью решения уравнений кинетики ядерного синтеза.
Горение термоядерного DT топлива описывается четырьмя основными ядерными реакциями:
D + T → 4He (3.52 MeV) + n (14.07 MeV), (2.15)
D + D → 3He (0.82 MeV) + n (2.45 MeV), (2.16)
D + D → T (1.01 MeV) + p (3.02 MeV), (2.17)
D + 3He → 4He (3.67 MeV) + p (14.68 MeV). (2.18)
Кинетика термоядерного горения для ядерных реакций (2.15) – (2.18) описывается уравнениями
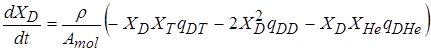, (2.19)
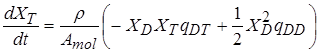, (2.20)
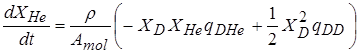, (2.21)
где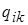 
– скорость соответствующей реакции. Скорости обеих реакций (2.16) и (2.17) считаются одинаковыми и равными 
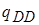. Величина 
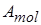определяется как 
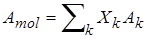, где индекс k относится к соответствующим атомам (ядрам) смеси.
Граничные условия задаются в следующем виде:
на оси симметрии, при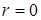 
ставятся условия нулевых градиентов
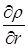u = 0, 
= 0,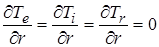 
, 
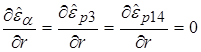; (2.22)
на внешней границе мишени, при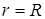 
ставятся условия
, 
, 
, 
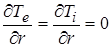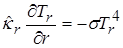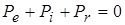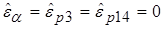. (2.23)
Результаты расчетов сжатия и горения мишени
Уравнения гидродинамики
Для описания процессов разлета мишени в камере и испарения защитной пленки первой стенки законы сохранения массы, импульса и энергии имеют вид [16, 17]
,
,
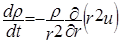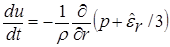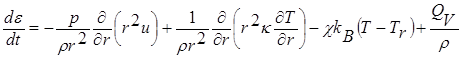, (4.1)
,
.
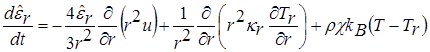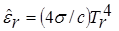Здесь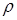 
– плотность, 
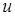– скорость, 
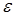– удельная внутренняя энергия вещества [Дж/кг], 
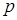– давление, 
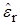– плотность энергии излучения [Дж/м3], 
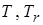– температуры соответственно вещества и излучения, 
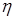– коэффициент вязкост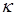и, 
и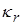 
– коэффициенты теплопроводности, 
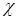– коэффициент температурной релаксации излучения и вещества, 
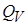– плотность энергии поглощения излучения в свинце. Обозначения универсальных постоянных: 
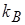– постоянная Больцмана, 
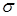– постоянная Стефана-Больцмана, 
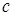– скорость света в вакууме.
4.3. Коэффициенты вязкости и теплопроводности
Коэффициент вязкости свинца в диапазоне 500-1000 К определяется по эмпирической зависимости [18]:
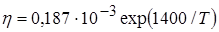. (4.2)
При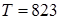 
К его значение равно 0,001 Па∙с. В отсутствие достоверных опытных данных при больших температурах вязкость положена равной нулю.
Коэффициент теплопроводности в веществе представляется в виде взвешенной суммы электронной и нейтральной компонент
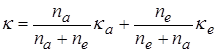, (4.3)
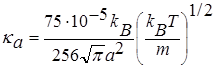, a = 1,8∙10-10 [м],
, 
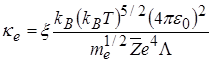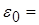8,85∙10-12 [СИ],
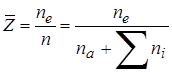, i=1,2,…,82,
где суммирование ведется по зарядовым состояниям иона свинца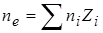 
, а параметр 
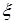слабо зависит от 
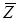(например, 
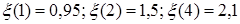). Кулоновский логарифм вычисляется по формуле 
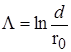, где
, 
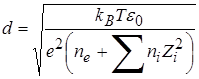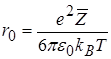. (4.4)
Коэффициент радиационной теплопроводности определяется по формуле [13]:
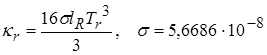[СИ]. (4.5)
Здесь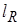 
есть средняя длина пробега по Росселанду:
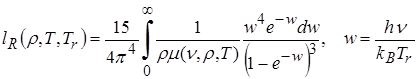, (4.6)
где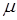 
– массовый коэффициент поглощения излучения в среде [см2/г], так что величина 
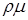имеет размерность обратной длины.
4.4. Коэффициенты поглощения и температурной релаксации
Релаксация между температурой электронов и температурой излучения описывается коэффициентом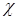 
в правой части (4.1). Этот коэффициент определяется в [11] по формуле
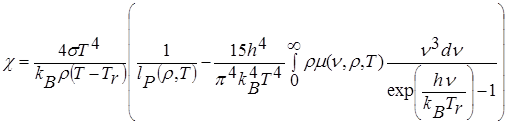, (4.7)
где средний планковский пробег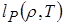 
определяется интегралом
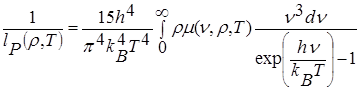. (4.8)
Таким образом,
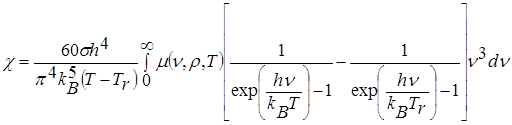. (4.9)
Формула (4.9) определяет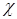 
как функцию плотности и двух температур – вещества и излучения. Однако двухтемпературная зависимость сильно усложняет процесс расчетов, поскольку для их проведения требуется табуляция 
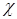путем численного интегрирования функционала (4.9) от эмпирической величины массового поглощения 
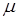. Будучи разложена в ряд по степеням 
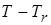, формула (4.9) в первом приближении дает независимость 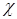от температуры излучения:
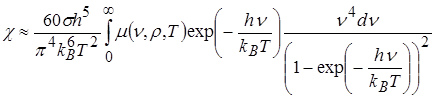. (4.10)
Таким образом, коэффициент релаксации приближенно можно записать в виде, аналогичном коэффициенту радиационной теплопроводности (4.5):
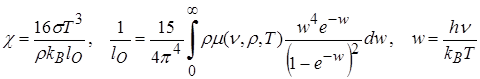. (4.11)
Нахождение величин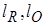 
связано с вычислением интегралов (4.6), (4.11), в которых спектральный коэффициент поглощения фотонов 
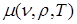в широкой области температур и плотностей для плазмы свинца был определен расчетным путем на основе программы THERMOS [14]. Указанные расчеты были проведены на основе релятивистской самосогласованной модели Хартри-Фока-Слэтера. В этой модели уровни энергий ионов и положения спектральных линий вычисляются в одноконфигурационном приближении Хартри-Фока. Вероятности различных состояний ионов определяются с использованием распределения Гиббса. В качестве профиля линий используется профиль Фойгта с учетом естественного уширения, уширения электронами, эффекта Штарка и эффекта Доплера, а также эффектов спин-орбитального расщепления методом Мошковского [19]. Расчет сечений фотоионизации проводится с использованием численных волновых функций электронов дискретного и непрерывного спектра, вычисленных в самосогласованном потенциале. При вычислении сечения тормозного поглощения используется модифицированная формула Борна-Эльверта с учетом эффектов вырождения. Комптоновское рассеяние вычисляется по уточненной формуле Клейна-Нишины.
Верификация программы THERMOS была проведена путем сопоставления с результатами расчетов по программам ведущих зарубежных центров – Ливерморской национальной лаборатории США (программы OPAL и HOPE), Лос-Аламосской национальной лаборатории США (программа LEDCOP), лаборатории Бер Шева из Израиля (программа STA). Проведены также сравнения с известными экспериментальными данными по измерению коэффициента прохождения (трансмиссии) для плазмы алюминия, железа, германия и гольмия [20]. Показано, что точность программы THERMOS при расчете детальных спектров достаточно высока. При расчете как детальных спектров, так и средних характеристик (в частности, усредненных по Плакнку и по Росселанду коэффициентов поглощения), получено хорошее согласие с наиболее продвинутыми зарубежными программами.
Пример расчетного коэффициента поглощения для плазмы свинца приведен на Рис. 11. Расчет проведен для температуры T=250 эВ и плотности ρ=10-2 г/см3. Весовая функция Планка соответствует штриховой линии, а весовая функция для вычисления величины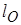 
обозначена пунктирной линией. Как видно из Рис. 11, использование весовой функции (4.11) смещает область влияния спектра поглощения в сторону больших энергий фотонов по сравнению с планковской весовой функцией (4.8).
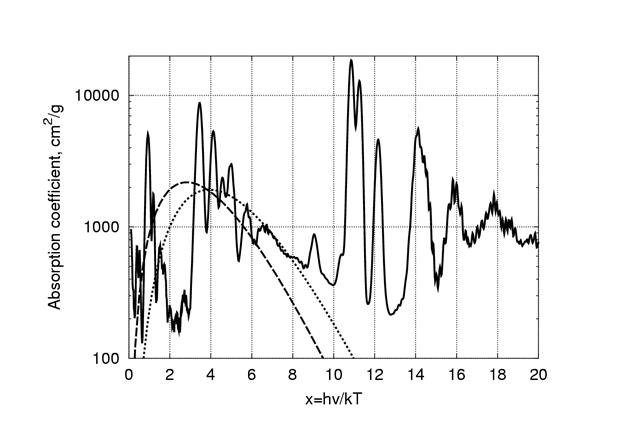
Рис. 11. Коэффициент поглощения в плазме свинца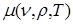 
при температуре T = 250 эВ и плотности ρ = 10-2 г/см3 (сплошная линия)
Усредненные с помощью весовой функции (4.11) величины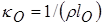 
в широкой области температур и плотностей представлены ниже на Рис. 12. Для удобства визуализации на графике представлены величины 
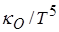. Характерная скейлинговая зависимость коэффициента 
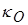от температуры и плотности среды в рассматриваемом диапазоне параметров приближенно может быть описана формулой ~ 
.
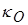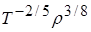Источниковый член в уравнении энергии (4.1) имеет вид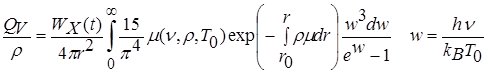 
. (4.12)
Здесь индексом 0 отмечены значения переменных на контактной поверхности между мишенью и атмосферой камеры. Контактная поверхность движется по траектории r0(t). Значения параметров WX(t) и Т0(t) берутся из расчетов по программе DEIRA-4 (см. графики на Рис. 10).
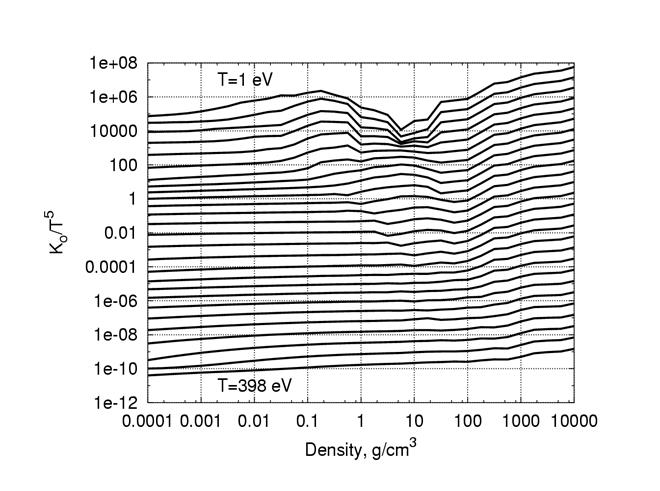
Рис. 12. Изотермы коэффициента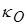 
в плазме свинца. Изотермы приведены с равномерным шагом по логарифму Т от 1 эВ до 398 эВ
Уравнение состояния
Широкодиапазонное уравнение состояния А.Б. Медведева [12] определяет зависимость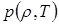 
неявным образом через подгоночный параметр – т.н. «объем коволюма» 
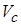. Само давление представляется в виде двух слагаемых – давления отталкивания 
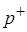и давления притяжения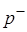 
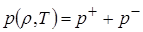, (4.13)
зависящих от 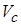. Ведем безразмерные величины 
, 
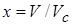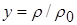, где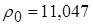 
г/см3 – некоторая постоянная, имеющая размерность плотности, своя для каждого вещества (в данном случае – для свинца). В модели [12] для свинца предложены следующие зависимости для определения 
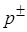[ГПа]:
- во всей области давлений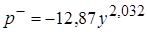 
;
- при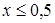 
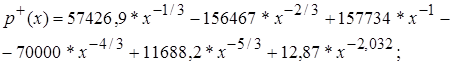
- в диапазоне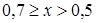 
применяется формула
;
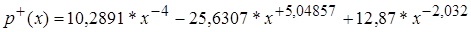- при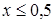 
.
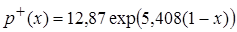Уравнение, которым определяется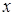 
, а, следовательно, по формулам, определенным выше, и давление 
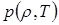, имеет вид:
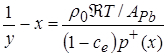. (4.14)
Здесь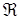 
– газовая постоянная, а 
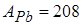– молярная масса свинца.
Система уравнений (4.13-4.14) показывает, что давление в модели в отсутствие ионизации определяется как функция температуры и плотности. По заданным значениям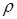 
и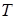 
из неявной зависимости (4.14) численно определяется значение виртуальной переменной 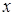, после чего по формуле (4.13) находится давление 
.
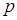С учетом ионизации в модель добавляется расчет концентрации ионов i-кратной ионизации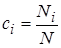 
, который проводится в предположении равновесия по формуле Саха:
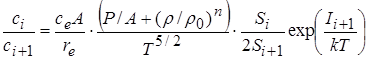, (4.15)
где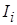 
– соответствующий потенциал ионизации свинца [13], 
, 
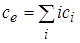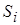– т.н. внутренняя статистическая сумма (в расчетах полагаем 
), 
.
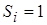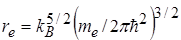Термическое уравнение состояния включает в себя энергию взаимодействия между частицами неидеальной среды, тепловую энергию и энергию ионизации:
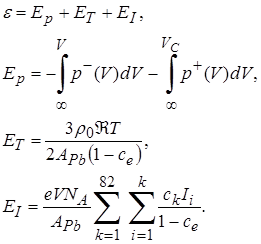(4.16)
Заключение
Моделирование полного сценария микровзрыва мишени и отклика камеры реактора на микровзрыв требует создания, по меньшей мере, двух различных гидродинамических кодов – одного для описания сжатия мишени, ее поджига и горения, и второго для описания разлета мишени, абляции первой стенки и взаимодействия встречных потоков вещества в камере. Это обусловлено принципиальным отличием физики процессов, протекающих на этих двух этапах, а также громадным отличием в них характерных масштабов времени, размеров, гидродинамических параметров и плотностей потоков массы импульса и энергии.
В данной работе моделирование микровзрыва мишени выполнено посредством последней версии кода DEIRA-4, а моделирование разлета мишени и отклика камеры реактора – с помощью вновь созданного кода радиационной гидродинамики. Сконструирована процедура сопряжения решений двух кодов с различной геометрией течения.
На основе кода DEIRA-4 осуществлен подбор энергетически эффективной мишени и режимных параметров тяжелоионных пучков, обеспечивающих требуемый уровень генерации термоядерной энергии в концепции ИТИС. Полностью определены временные профили потоков энергии, переносимых нейтронами, заряженными частицами и излучением в процессе микровзрыва, а также поля гидродинамических переменных в момент выхода ударной волны на свободную поверхность мишени.
В данной работе представлена модель и результаты численного сопряженного расчета разлета мишени в камере и воздействия продуктов термоядерного микровзрыва на первую стенку камеры реактора. Важность этой части работы заключается в том, что в ней впервые проведены численные расчеты отклика камеры реактора на микровзрыв в рамках одной программной реализации, позволяющей решать систему уравнений гидродинамики и переноса излучения не только для аномально высоких плотностей энергии (как непосредственно в фаерболе), но и для экстремальных условий (абляция жидкой пленки), а также в разреженной атмосфере камеры.
Благодарности
Авторы отмечают решающее влияние на эту работу академика В.И. Субботину, инициировавшему в Научном Совете РАН по физико-техническому анализу энергетических систем разработку концепции ИТИС. Авторы также глубоко благодарны члену-корреспонденту А.В. Забродину, руководившему работами по концепции ИТИС в ИПМ РАН, за поддержку и постоянное внимание к проводимым исследованиям.
Мы выражаем признательность академику В.П. Смирнову и члену-корреспонденту Б.Ю. Шаркову за многочисленные плодотворные обсуждения затрагиваемых вопросов. Мы также благодарим докторов физико-математических наук М.В. Масленникова и С.Л. Недосеева за критические замечания, полезные советы и ценные замечания по работе в ходе дискуссий на научных семинарах по проблемам ИТС.
Особую благодарность авторы выражают доктору физико-математических наук В.Г. Новикову за проведение расчетов коэффициента поглощения излучения в плазме свинца и релаксационного члена в однотемпературном приближении.
Литература
1. Medin S.A., Churazov M.D., Koshkarev D.G. et al. Evaluation of a power plant concept for fast ignition heavy ion fusion // Laser and Particle Beams, 2002. V.20, p.419–423.
2. Basko M. M., Churazov M. D., Aksenov A. G. Prospects of heavy ion fusion in cylindrical geometry. // Laser and Particle Beams, 2002. V.20, p.411–414.
3. Medin S.A., Churazov M.D., Koshkarev D.G., et al. Reactor Chamber and Balance-of-Plant Characteristics for Fast-Ignition Heavy-Ion Fusion Power Plant // Fusion Science and Technology, 2003. V.43, No.3, p.437–446.
4. Медин С.А., Орлов Ю.Н., Суслин В.М., Паршиков А.Н. Моделирование отклика первой стенки камеры и бланкета реактора ИТС на микровзрыв. / Препринт ИПМ им. М.В. Келдыша РАН, № 41, 2004.
5. Медин С.А., Орлов Ю.Н. Концепция камеры реактора ИТС на тяжелых ионах // ВАНТ, сер. Термоядерный синтез, 2005. Вып. 2. С. 3-14.
6. Medin S.A., Basko M.M., Koshkarev D.G., Orlov Yu.N., Parshikov A.N., Sharkov B.Yu., Suslin V.M. Power Plant Design and Accelerator Technology for Heavy Ion Inertial Fusion Energy // Nuclear Fusion, 2005. V. 45. S291-S297.
7. Koshkarev D.G. Charge-Symmetric Driver for Heavy-Ion Fusion. // IL Nuovo Chimento, 1993. Vol.106 A, No.11, p.1567–1571.
8. Кошкарев Д.Г., Чуразов М.Д., Баско М.М. и др. Мощный тяжелоионный драйвер для зажигания термоядерной ДТ мишени. / Препринт ИТЭФ, 4-01, 2001.
9. Чуразов M.Д., Аксенов A.Г., Забродина E.A. Зажигание термоядерных мишеней пучком тяжелых ионов. // ВАНТ, Сер. Математические модели физических процессов, 2001. Вып. 1, №.20, с.1–13.
10. Долголева Г.В., Забродин А.В. Кумуляция энергии в слоистых системах и реализация безударного сжатия. М.: Физматлит, 2004, 70 с.
11. Basko M.M. DEIRA 1D-3T hydrodynamic code for simulating ICF targets driven by fast ion beams. / Moscow: ITEP, 2001.
12. Медведев А.Б. Модификация модели Ван-дер-Ваальса для плотных состояний. / В сб.: Ударные волны и экстремальные состояния вещества. Под ред. В.Е. Фортова, Л.В. Альтшулера, Р.Ф. Трунина и А.И. Фунтикова. М.: Наука, 2000.
13. Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971.
14. Никифоров А.Ф., Новиков В.Г., Уваров В.Б. Квантово-статистические модели высокотемпературной плазмы и методы расчета росселандовых пробегов и уравнений состояния. М.: Физматлит, 2000.
15. Hubbell J.H., Seltzer S.M. Tables of X-Ray Mass Attenuation Coefficients. NIST, 1996.
16. Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных гидродинамических явлений. М.: Наука, 1966.
17. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика VI. Гидродинамика. М.: Наука, 1988.
18. dai Kai Sze, Ralph Moir, Steve Zinkle. Data Base for Liquid Breeders and Coolants. / APEX Interim Report, November, 1999.
19. Драгалов В.В., Никифоров А.Ф., Новиков В.Г., Уваров В.Б., Статистический метод расчета поглощения фотонов в плотной высокотемпературной плазме, Физика плазмы, 1990, т.16, № 1, с.77-85.
20. Новиков В.Г., Никифоров А.Ф., Уваров В.Б., Драгалов В.В. Поглощение фотонов в высокотемпературной плазме. / Препринт ИПМ им. М.В. Келдыша РАН, № 17, 1992. – 22 с.
21. Самарский А.А., Попов Ю.П. Разностные методы решения задач газовой динамики. М.: Наука, 1980.
22. Медин С.А., Орлов Ю.Н., Суслин В.М. Расчет динамики испарения защитной пленки первой стенки камеры реактора ИТС / Препринт ИПМ им. М.В. Келдыша РАН, № 62, 2004. – 28 с.
23. S.A. Medin, M.M. Basko, Yu.N. Orlov and V.M. Suslin. X-ray and Ion Debris Impact on the First Wetted Wall of IFE Reactor. / 33-d European Physical Society Conference on Plasma Physics. Roma, Italy, June 19-23, 2006. Collected abstracts, p.32.
Содержание
1. Введение ……………………………………………………………………...4
1.1. Концепция тяжелоионного DT-синтеза с быстрым поджигом ………....4
1.2. Базовые пераметры ЯЭУ на основе тяжелоионного DT-синтеза …….…5
2. Физико-математическая модель сжатия и горения мишени …....................7
2.1. Взамодействие тяжелоионного пучка с оболочкой мишени ………….…7
2.2. Уравнения сохранения трехтемпературной гидродинамической
модели ……………………………………………………………………….8
2.3. Уравнения диффузии заряженных частиц и кинетики
термоядерного горения …………………………………………….……...10
3. Результаты расчетов сжатия и горения мишени …………………………...11
3.1. Динамика сжатия мишени цилиндрическим пучком ……………………11
3.2. Выход ударной волны на поверхность мишени, генерация
импульсов энергии нейтронов и рентгеновского излучения …………...13
4. Физико-математическая модель разлета мишени и испарения
защитной жидкой пленки первой стенки камеры …………………………….16
4.1. Сценарий разлета мишени и испарения защитной пленки .…………......16
4.2. Уравнения гидродинамики ………………………………………………...18
4.3. Коэффициенты вязкости и теплопроводности ……………………………19
4.4. Коэффициенты поглощения и температурной релаксации ………………20
4.5. Уравнение состояния ………………………………………………………..23
4.6. Начальные и граничные условия для расчета разлета мишени
и абляции жидкой пленки …………………………………………………..24
4.7. Алгоритм расчета и численная схема ……………………………………...25
5. Результаты расчетов разлета мишени и абляции жидкой пленки ….............26
5.1. Отклик жидкой пленки на воздействие рентгеновского
пред-импульса и нейтронного потока ……………………………………...26
5.2. Разлет облака мишени и абляция жидкой пленки …………………………27
6. Заключение …………………………………………………………………….34
Благодарности ……………………………………………………………………34
Литература………………………………………………………………………...35
ВВЕДЕНИЕ
Концепция тяжелоионного DT-синтеза с быстрым поджигом
Настоящая работа является продолжением исследований [1-6], в ходе которых была предложена концепция энергетической установки на основе тяжелоионного DT-синтеза, а также были проведены численные расчеты, показывающие согласованность физических параметров, определяющих технологическую схему такой установки.
Кратко опишем содержание концепции ИТИС (FIHIF), следуя [1, 5, 6].
В работах [2, 7, 8] предполагается, что можно построить мощный тяжелоионный ускоритель, позволяющий ускорять однозарядные ионы тяжелых металлов до энергии ~500 МэВ/на нуклон (~100 ГэВ/на ядро). Пучок ионов облучает с торца цилиндрическую мишень [2, 9], на оси которой находится термоядерное топливо (эквимолярная смесь DT), окруженное свинцовой оболочкой (Рис. 1). Пятно пучка перемещается по торцу мишени по окружности с частотой ~109 Гц, обеспечивая практически однородное по азимуту выделение энергии в кольцевом слое (абсорбере) оболочки. Мощность пучка профилируется по времени так, чтобы энерговыделение в абсорбере обеспечило безударное сжатие топлива [10]. При достижении максимального сжатия DT-топливо поджигается сверхмощным пучком, сфокусированным на торец DT-шнура (режим быстрого поджига). Мишени инжектируются в камеру, где происходит микровзрыв, с частотой 2 Гц.
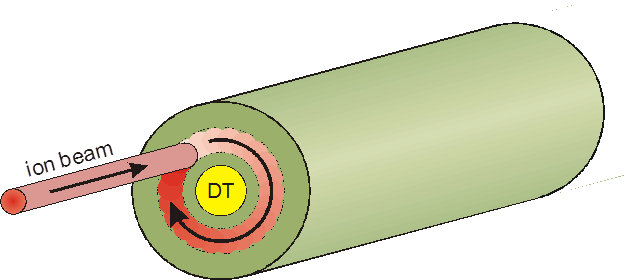
Рис. 1. Цилиндрическая мишень в концепции ИТИС и ее облучение
ионным пучком на стадии сжатия
Для предложенного сочетания драйвера и мишени в работах [1, 5, 6] представлены общая схема реакторной камеры (включая первую стенку и бланкет) и тепловая схема электростанции. Первая стенка камеры выполнена из пористого карбида кремния. Через поры в камеру просачивается жидкометаллический теплоноситель (эвтектика свинец-литий), образующий защитную пленку. В нижней части камеры сделана конденсационная полость, в которую тот же теплоноситель инжектируется в виде спрэя для ускорения процесса конденсации вещества, испаренного в результате микровзрыва.
Одномерные расчеты сжатия цилиндрической мишени и двумерные расчеты ее последующего воспламенения были выполнены в работе [2]. Моделирование воздействия продуктов термоядерного микровзрыва на первую стенку камеры и конструкционные материалы бланкета реактора ИТИС было проведено в работах [4, 5] в одномерной плоской геометрии и без учета переноса излучения. В настоящей работе мы представляем результаты согласованных расчетов сжатия и горения мишени в цилиндрической постановке, а также разлет мишени - с учетом переноса нейтронов и излучения, а также отклика первой стенки камеры реактора на микровзрыв в сферически-симметричной постановке задачи.
Следует подчеркнуть, что представляемые в данной работе расчеты носят теоретический характер и не имеют верификации в части горения термоядерной мишени и, соответственно, отклика камеры на микровзрыв, поскольку требуемые параметры драйвера в настоящее время не достижимы. Кроме того, численный расчет горения и разлета носит качественный характер и не является инженерным, учитывающим реальную геометрию объекта. Целью работы было проведение сквозного расчета горения мишени, ее разлета и взаимодействия продуктов микровзрыва с материалом первой стенки камеры в идеальной математической постановке задачи, но с возможно более полной физической системой уравнений. Полученные результаты показывают, что такой расчет может быть корректно проведен. Это позволяет надеяться и на возможность проведения таких расчетов в реальной геометрии.
Дата: 2019-12-10, просмотров: 216.
