В настоящем разделе приведен вывод выражения для мощности сигнала на выходе приёмной антенны при зондировании отражателя – модулятора передатчиком. Расстояние между антенной передатчика и модулятора полагается равным R1, между модулятором и антенной приёмника – R2. В качестве сигнала рассматривается колебание, создаваемое в точке приёма за счёт переизлучения части энергии, наводимой в полуволновом вибраторе первичным полем. Кроме указанной составляющей в точке приёма существует ещё колебание, создаваемое непосредственным прохождением излучённой волны в точку приёма.
Однако в отличие от первой, эта составляющая не может быть модулирована сигналом, поступающим на отражатель – модулятор. Поскольку помехоустойчивость обработки по отношению к аддитивным помехам определяется суммарной мощностью боковых колебаний РБОК= m 2 × РС (где m - полный индекс амплитудно-фазовой модуляции, РС – мощность несущего колебания), то, найдя индекс модуляции m и мощность сигнала РС, поступающего от диполя при отсутствии модуляции, параметр РБОК определяется полностью, и мощность сигнала прямого прохождения сигнала не имеет значения.
Как показано выше (4.4), амплитуда ЭДС, наведённой полем зондирующего сигнала, равна:
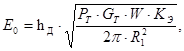(4.4)
Амплитуда тока первой гармоники, вызванной действием ЭДС Е0, определяется равенством:
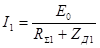, (6.1)
где ZД1 – сопротивление диода по первой гармонике тока вибратора;
R S 1 - сопротивление излучения вибратора на первой гармонике.
Мощность сигнала переизлучаемая вибратором на k – ой гармонике определяется выражением:
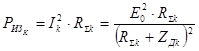, (6.2)
Подставляя в (6.2) выражение (4.4) для амплитуды ЭДС Е0 , можно получить:
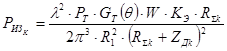, (6.3)
где
PИЗк – мощность, излучённая отражателем модулятором на k - ой гармонике;
PT,GT( q) – мощность передатчика и коэффициент направленного действия его антенны;
W=120 p - волновое сопротивление свободного пространства;
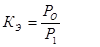- отношение потоков мощности поступающего на экран сигнала и сигнала, прошедшего через экран – коэффициент экранировки.
Мощность сигнала на выходе приёмной антенны при условии идеального её согласования с приёмником на k – ой гармоники равна:
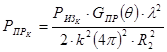, (6.4)
где GПР( q) – коэффициент направленного действия антенны для k – гармоники;
k – номер гармоники.
Подставляя в (6.4) соотношение (6.3), можно получить окончательное выражение для мощности сигнала на входе приёмника:
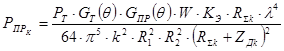, (6.5)
Полученное соотношение позволяет оценить мощность сигнала на входе приёмника в зависимости от расстояния меду антенной передатчика и отражателем- модулятором, от расстояния между отражателем – модулятором и антенной приёмника, с учётом диаграмм направленности передающей и приёмной антенны, для различных гармоник зондирующего сигнала. С использованием соотношений раздела 4 можно получить мощность для полезного сигнала на входе приёмника.
ЗАКЛЮЧЕНИЕ
1) В данной дипломной работе был разработан приближённый метод для моделирования отражателя – модулятора, который может быть использован для получения количественных и качественных характеристик модуляции, полученной в данном устройстве. Метод позволяет найти коэффициенты модуляции на трёх гармониках зондирующего сигнала, коэффициенты относительной нелинейной модуляции и токи в симметричном вибраторе отражателя-модулятора также на всех трёх гармониках.
2) В дипломной работе разработана методика моделирования симметричного вибратора эквивалентной схемной функцией электрической цепи. Были выведены формулы для получения коэффициентов схемной функции, которые приведены в ПРИЛОЖЕНИИ 1. Эти формулы были проверены и показали свою полную состоятельность. Подобный метод моделирования симметричного вибратора не встречался ещё ни в одной литературе, которая была бы посвящена вопросам моделирования. С использованием этой модели открываются большие возможности моделирования антенн при помощи специализированных пакетов расчёта электрических цепей. Кроме того, эта модель помогла понять суть процессов, протекающих в вибраторе, которые до этого во времени излагались не совсем корректно.
3) В этой работе была совершена попытка некого эвристического синтеза электрических схем по заданной схемной функции. Пока ещё трудно сказать, действительно ли этот способ синтеза справедлив во всех случаях для положительной вещественной функции двухполюсника, однако ясно пока одно, что с его помощью можно получить простые и изящные реализации RLC-двухполюсников, чем, например, используя метод Бруне, который требует значительных вычислительных затрат.
4) Проведён упрощённый теоретический анализ модулятора на диоде, с использованием аппроксимации его вольтамперной характеристики полиномом четвёртой степени. В ходе этого анализа была обнаружена ошибка в выводах дипломной работы предыдущего года, посвящённой этой же теме. Согласно выводам, полученным в данной дипломной работе, использование отражателя-модулятора на диоде ничуть не дороже, с энергетической точки зрения источника напряжения смещения, чем использование в отражателе-модуляторе варикапа. Были получены формулы для вывода требуемых напряжений источников сигнала, исходя из заданных коэффициентов модуляции, которые говорят, что можно получить сравнительно большие коэффициенты модуляции (10%) при сравнительно не больших нелинейных искажениях (10%). Более того, эти формулы были подтверждены моделированием отражателя-модулятора на ПЭВМ, потому что максимальная разница в расчётах составила порядка 25%, что является хорошим приближением.
5) Был уточнён расчёт энергетических характеристик системы перехвата в целом. С учётом расстояний до зондирующего передатчика и приёмника, возможным экранированием пространства, различными диаграммами направленности симметричного вибратора на разных гармониках зондирующего сигнала.
6) Была разработана мощная программа для моделирования трёх реализаций отражателя-модулятора (одна для диода, две для варикапа). Программа позволяет моделировать симметричный вибратор по заданным его характеристикам на трёх кратных частотах, синтезирует его эквивалентную электрическую схему, позволяет менять различные параметры остальных элементов устройства, позволяет задавать все сигналы в аналитическом в виде, что делает её не заменимым инструментом при исследовании отражателя-модулятора. Программа показала результаты, которые полностью отвечают теоретическим исследованиям, и явилась их наглядным пособием.
7) В работе были описаны меры для предотвращения неблагоприятного воздействия на человека вредных факторов, связанных с работой на персональных электронно-вычислительных машинах, определены санитарно-гигиенические требования, предъявляемые к условиям работы на компьютере.
8) Моделирование устройства на ПЭВМ позволило сэкономить значительные денежные средства и сделало работу по исследованию более гибкой и не долгой по времени, что явилось причиной её сравнительно дешевизны.
Дальнейшее использование выводов и моделей, разработанных в этой работе позволить получить более качественные отражатели-модуляторы с оптимальными характеристиками, кроме того, появиться возможность реального моделирования на ПЭВМ процессов обработки сигналов, полученных в модели отражателя-модулятора.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Харкевич А.А. Основы радиотехники М.: «Связьиздат», 1962г. – 560с.
2. Моделирование в радиолокации/ А.И. Леонов, В.Н. Васенёв, Ю.И. Гайдуков и т.д.; Под ред. А.И. Леонова. – М.:Сов. Радио, 1979г., 264с.
3. Громаков Ю.А. Стандарты и системы подвижной радиосвязи М.: 1996г. 239с.
4. Попереченко Б.А. Антенно-фидерные устройства: Часть I. Теория излучения и приёма радиоволн. М.: 1961г. МЭИ. 135с.
5. Астрецов Д.В., Болотов Ю.Н. Методы анализа нелинейных и цифровых следящих систем. Учебное пособие. Екатеринбург: УГТУ-УПИ. 1993г.
6. Цифровая обработка сигналов: Учебное пособие для вузов/ Гольденберг Л.М., Матюшкин Б.Д., Поляк М.Н. – 2 изд., перераб. и доп. – М.: Радио и связь. 1990г. 256с.
7. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. – 4-е изд., перераб. и доп.- М.: Радио и связь, 1986г. 512с.
8. Радиоэлектронные системы: Методические указания к дипломному проектированию/ Астрецов Д.В., Лысенко Т.М. Екатеринбург: УГТУ-УПИ, 1995г. 36с.
9. Моделирование линейного инерционного звена второго порядка. Методические указания к лабораторным работам по курсу «Цифровое моделирование радиоэлектронных систем»./ Дмитриев С.Н. Свердловск: УПИ, 1990г. 19с.
ПРИЛОЖЕНИЕ 1. Основные расчётные формулы для вычисления коэффициентов.
 |
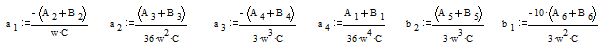ПРИЛОЖЕНИЕ 2.
Дата: 2019-12-10, просмотров: 263.
