Из курса «Теория радиотехнических сигналов и цепей» известно, что RLC – двухполюсник имеет схемную функцию в виде рациональной дроби, степень знаменателя и числителя которой отличаются, не более чем на единицу, иначе импульсная характеристика цепи будет стремиться в бесконечность при конечной мощности входного воздействия. Кроме того, функция входного сопротивления или проводимости RLC – цепи имеет в числителе и знаменателе все степени. В некоторых случаях, когда полное сопротивление в нуле стремиться к нулю или бесконечности, может отсутствовать нулевая степень, т.е. нулевой коэффициент равен нулю.

Ниже на рис. 3.4 приведены экспериментальные графики для входного сопротивления вибратора [4]. На верхнем графике рисунка приведены зависимости активной части входного сопротивления от отношения длины вибратора к длине волны. Эта зависимость пропорциональна зависимости сопротивления от частоты при постоянной длине вибратора (частота обратно пропорциональна длине волны). На нижнем графике рисунка видим зависимость реактивной части сопротивления от частоты. Заметим, что на нулевой частоте (l=¥) значение реактивной составляющей стремится в “минус” бесконечность, значит, у нас в знаменателе полного сопротивления отсутствует нулевая степень.

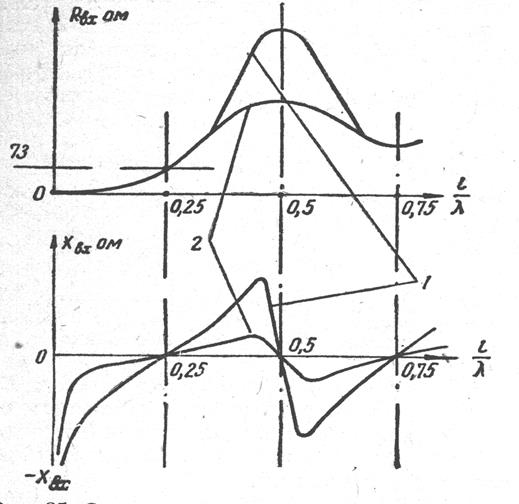
Рис 3.4. Зависимость входного сопротивления симметричного вибратора от его длины при различном волновом сопротивлении вибратора (см. главу 2.2): кривая 1 – для W_B1; кривая 2 – для W_B2 , где W_B1 > W_B2 .

Видим, что первым на оси часто стоит последовательный резонанс, затем параллельный и т.д., т.е. вибратор обладает таким свойством RLC – цепи, как чередование нулей и полюсов. Понятие «полюс», в данном случае, подразумевает наличие параллельного резонанса, хотя реактивная составляющая и равна нулю на этой частоте (это связано с наличием потерь в вибраторе на излучение). Так как вибратор обладает свойством чередования нулей и полюсов, то мы можем записать схемную функцию RLC – цепи и, подбором коэффициентов её полиномов числителя и знаменателя, добиться приближения её параметров на частотах кратных частоте зондирующего сигнал к параметрам вибратора.

В дипломной работе рассматривается работа вибратора до третей гармоники зондирующего сигнала. По условию задачи, для частоты зондирующего сигнала вибратор является полуволновым, т.е. на частоте зондирующего сигнала работа вибратора аналогична работе последовательного контура, отсюда работа вибратора на второй и третей гармонике облучающего сигнала аналогична работе параллельного и последовательного контура соответственно.

Исходя из выше сказанного, делаем вывод, что наша схемная функция имеет два «нуля» на комплексной плоскости (плюс ещё два из-за комплексной сопряжённости, причём каждый нуль имеет вид: ((p-a)²+b²)), один «полюс» на комплексной плоскости и один «полюс» в нуле. Под «полюсом» на комплексной плоскости понимается наличие параллельного резонанса (системная функция в этой точке имеет конечное значение), под «нулём» - наличие последовательного резонанса.

Следовательно, требуемая схемная функция будет иметь в числителе полином четвёртого порядка, а в знаменателе полином третьего порядка, у которого будет отсутствовать свободный член.

Построение схемной функции

В предыдущем подразделе мы выяснили, какой вид должна иметь схемная функция RLC – двухполюсника, имеющей два последовательных резонанса, один параллельный, и в нуле эквивалентна ёмкости:

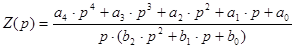,            (3.1)

Получили восемь неизвестных коэффициентов, которые необходимо найти. Кроме того, можно показать, что любой RLC – двухполюсник, не имеющий перекрёстных связей, имеет функцию сопротивления или проводимости вида (3.1), у которой коэффициенты a₀=b₀=1. Отсюда, имеем шесть неизвестных коэффициентов, для нахождения которых нам потребуется шесть уравнений. Предложим следующий вариант системы уравнений, из которой можно найти коэффициенты (3.1).

Найдём активные и реактивные составляющие сопротивления (3.1) на трёх гармониках и при равняем их составляющим сопротивления вибратора на этих же гармониках. Получается, что мы провели кривую, заданную выражением (3.1), через три точки полного сопротивления вибратора. Эти точки возьмём на частотах кратных частоте облучающего сигнала. Таким образом, мы гарантировано имеем те же значения сопротивления (3.1) на требуемых частотах.