Excel также позволяет, кроме численное решение уравнения от одной неизвестной, еще и решать более сложные задачи оптимизации. Решения задачи, удовлетворяющие всем ограничениям и граничным условиям, называются допустимыми. Оптимальное решение - (optimus от лат. наилучший) это наилучшее решение, но наилучшего решения во всех смыслах быть не может. Может быть лучшим только в одном, строго установленном смысле. Принимающий решение должен абсолютно точно представлять, в чем заключается оптимальность решения, т.е. по какому критерию (kriterio - мерило, оценка) принимаемое решение должно быть оптимальным. Например, необходимо найти экстремум (минимум или максимум) функции от нескольких переменных, на которые могут быть наложены условия ограничения (например, только целочисленные значения). При этом критерий называют целевой функцией (ЦФ). С помощью критерия можно оценивать качества как желательные (например прибыль, производительность, надежность), так и нежелательные (затраты, расходы, простои и т.д.). Тогда в первом случае стремятся к максимизации критерия, во втором - к минимизации.
Итак, задача имеет оптимальное решение, если она удовлетворяет двум требованиям:
§ есть реальная возможность иметь более одного решения, т.е. существуют допустимые решения;
§ имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т.е. наилучшим из допустимых.
В качестве примера, решим следующую задачу:
Задача. Завод производит электронные приборы трех видов (прибор А, прибор В и прибор С), используя при их сборке микросхемы трех видов (тип 1, тип 2 и тип 3). Расход микросхем задается следующей таблицей:
| Прибор А | Прибор В | Прибор С | |
| Тип-1 | 2 | 5 | 1 |
| Тип 2 | 2 | 0 | 4 |
| ТипЗ | 2 | 1 | 1 |
Стоимость изготовленных приборов одинакова.
Ежедневно на склад завода поступает 500 микросхем типа 1 и по 400 микросхем типов 2 и 3. Каково оптимальное соотношение дневного производства приборов различного типа, если производственные мощности завода позволяют использовать запас поступивших микросхем полностью?
1. Запустите программу Excel (Пуск > Программы > Microsoft Excel) и откройте рабочую книгу book.xis, созданную ранее.
2. Создайте новый рабочий лист (Вставка > Лист), дважды щелкните на его ярлычке и присвойте ему имя Организация производства.
3. В ячейки А2, A3 и А4 занесите дневной запас комплектующих числа 500,400 и 400, соответственно.
4. В ячейки С1, D1 и Е1 занесите нули. В этих ячейках будут находиться величины дневного производства для данных трех приборов. Нули мы заносим в качестве первоначального приближения к решению. В дальнейшем значения этих ячеек будут подобраны автоматически.
5. В ячейках диапазона С2:Е4 разместите таблицу расхода комплектующих.
6. В ячейках В2:В4 нужно указать формулы для расчета расхода комплектующих по типам. В ячейке В2 формула будет иметь вид =$С$1*C2+$D$1*D2+$E$1*E2, а остальные формулы можно получить методом автозаполнения (обратите внимание на использование абсолютных и относительных ссылок).
7. В ячейку F1 (целевую ячейку) занесите формулу, вычисляющую общее число произведенных приборов: для этого выделите диапазон С1 :Е1 и щелкните на кнопке Автосумма на стандартной панели инструментов. Мы будем искать экстремальное значение (максимум) для данной ячейки при всех ограничениях задачи.
8. Дайте команду Сервис > Поиск решения. Откроется диалоговое окно Поиск решения
Примечание. Если вы не увидите данной команды, вам необходимо еще раз войти в меню Сервис и , далее, в Надстройки. Далее необходимо поставить галочку напротив Поиск решения, см. рис.:
 9. В поле Установить целевую укажите ячейку, содержащую оптимизируемое значение (F1). Установите переключатель Равной максимальному значению (требуется максимальный объем производства).
9. В поле Установить целевую укажите ячейку, содержащую оптимизируемое значение (F1). Установите переключатель Равной максимальному значению (требуется максимальный объем производства).
10. В поле Изменяя ячейки задайте диапазон подбираемых параметров С1:Е1.
11. Чтобы определить набор ограничений, щелкните на кнопке Добавить. В диалоговом окне Добавление ограничения в поле Ссылка на ячейку укажите диапазон В2:В4. В качестве условия задайте <=. В поле Ограничение задайте диапазон А2:А4. Это условие указывает, что дневной расход комплектующих не должен превосходить запасов. Щелкните на кнопке ОК.
12. Снова щелкните на кнопке Добавить. В поле Ссылка на ячейку укажите диапазон С1:Е1. В качестве условия задайте >=. В поле Ограничение задайте число 0. Это условие указывает, что число производимых приборов неотрицательно. Щелкните на кнопке ОК.
13. Снова щелкните на кнопке Добавить. В поле Ссылка на ячейку укажите диапазон С1:Е1. В качестве условия выберите пункт цел. Это условие не позволяет производить доли приборов. Щелкните на кнопке ОК.
14. Щелкните на кнопке Выполнить. По завершении оптимизации откроется диалоговое окно Результаты поиска решения.
15. Установите переключатель Сохранить найденное решение, после чего щелкните на кнопке ОК.
16. Проанализируйте полученное решение. Кажется ли оно очевидным? Проверьте его оптимальность, экспериментируя со значениями ячеек С1:Е1. Чтобы восстановить оптимальные значения, можно в любой момент повторить операцию поиска решения.
17. Сохраните рабочую книгу.
V. Индивидуальное Задание:
Общие требования к заданию:
Все задание выполняется в одной рабочей книге Excel. Имя книги включает фамилию студента и номер группы - например, "Иванов_С_04.xls". Каждый пункт задания выполняется на отдельном рабочем листе.
Все части документа должны быть созданы в Excel. Ячейки таблиц, предполагающие вычисления, должны быть заполнены вычисляемыми полями формул. Форматирование рабочих листов должно соответствовать образцу.
Защита работы может включать в себя дополнительные задания, касающиеся изученных возможностей Microsoft Excel.
Номер варианта определяется по последней цифре студ. билета (зачетки). Цифре 0 соответствует 1й вариант, 1-2й вариант и т.д.
Задание 1. Базовые возможности Excel.
1) Первый лист рабочей книги назвать "Таблица значений функции". Используя копирование, автозаполнение и расчет по формуле, создать таблицу значений функции, указанной в Вашем варианте задания. Таблица должна иметь заголовок следующего вида:
| Таблица значений функции F(x,y)=x2+y2 | ||
| X | Y | F(x,y) |
| 1 | 1 | 2 |
| … | … | … |
Y в таблице меняется быстрее, чем X. На этом же листе построить график функции f(x1,y) по табличным данным, где x1 - начальное значение x.
Для этой же функции представить таблицу значений в виде
| x1 | … | xm | |
| y1 | f(x1, y1) | … | f(x1, ym) |
| … | … | … | … |
| yn | f(xn, y1) | … | f(xn, ym) |
При копировании формул использовать смешанные ссылки. По данным этой таблицы построить график поверхности f(x,y)
Таблица вариантов
| № варианта | функция f(x,y) | значения x | значения y |
| 1. | sin x2 + xy | 0, 0.1, …., 0.5 | 1,2,3,4,5 |
| 2. | 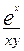
| 1,2,3 | 0.5, 1, …, 2.5 |
| 3. | 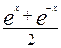
| -2,-1,…,2 | -2,-1,…,2 |
| 4. | 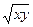
| 0.1, 0.2,…,0.4 | 0.1, 0.2,…,0.4 |
| 5. | 2x2-4y3 | 1,2,…,5 | 1,2,…,5 |
| 6. | 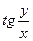
| 0.1, 0.3, …, 0.7 | 1,2,3,4 |
| 7. | 2e2x - sin y4 | 1,2,3,4,5 | 0, 0.1, …., 0.5 |
| 8. | 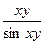
| -1, -0.5, …, 1 | -1, -0.5, …, 1 |
| 9. | 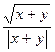
| -2, -1, …, 2 | -2, -1, …, 2 |
| 10. | cos 4x + sin 2y | 0, 0.2, …, 1 | 0, 0.2, …, 1 |
2) Второй лист рабочей книги назвать "Зарплата". Подготовить таблицу данных с заголовком вида
| ФИО | Начислено | Ставка налога, % | Налог в пенсионный фонд, 1% | К выдаче |
Ширину поля ФИО задать вдвое большей, чем остальных полей.
Три последних столбца - вычисляемые.
Ставка налога вычисляется по формуле:
12%, если зарплата менее 6000 руб.;
15%, в противном случае.
Сумма к выдаче рассчитывается как "Начислено" - "Ставка налога" - "Налог в пенсиононный фонд".
Ввести в таблицу 5-6 записей о студентах группы.
 |
3) Создать третий лист с именем "Прайс-лист" по образцу:
Поля "Цена, у.е." и "Сумма" - вычисляемые. В поле "Сегодня" автоматически подставляется текущая дата.
Заполнить прайс на 6-7 товаров.
Задание 2. Работа с функциями и формулами.
1) Создать рабочий лист с названием "Расчеты по формулам". Используя математические, логические и статистические функции Excel, вычислить таблицу значений функции, указанной в Вашем варианте.
С помощью формул подсчитать сумму и количество положительных и отрицательных значений Вашей функции, найти ее минимальное и максимальное значения на области определения.
Таблица вариантов
| № варианта | функция | значения аргументов и величин |
| 1. | 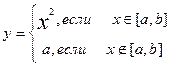
| a=0, b=1 x=-1,0.5,…,2 |
| 2. | 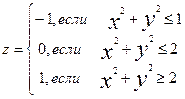
| x=0,0.5,..,2 y=0,0.5,..,2 |
| 3. | 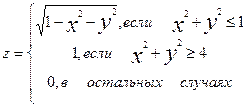
| 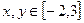 , шаг по x и по y = 0,5 , шаг по x и по y = 0,5
|
| 4. | 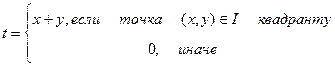
| x=-1,0,1, y=-2,-1,…,2 |
| 5. | z=max2(x,y)+min(|x|,|y|,0) | x,y меняются от -3 до 3 с шагом 0,5 |
| 6. | z=x, если x и y - четные, z=y, если x и y - нечетные, z=0, в остальных случаях | x,y меняются от 1 до 6 с шагом 1 |
| 7. | 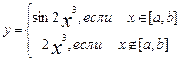
| a=-1, b=1 x=-3,-2,…,3 |
| 8. | 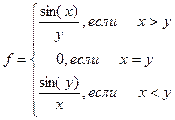
| 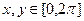 , шаг по x,y= , шаг по x,y= 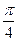
|
| 9. | 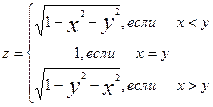
|  , шаг по x,y=0.2 , шаг по x,y=0.2
|
| 10. | Z=10-(x2+y2), если точка (x,y) принадлежит кругу радиуса 3 с центром в н начале координат; z=0, в противном случае | x,y меняются от -4 до 4 с шагом 1 |
Задание 3. Работа с матрицами и векторами.
1) Подготовить рабочий лист "Решение системы уравнений", на котором решить систему линейных уравнений вида Ax=b. Матрицу A и вектор b сформировать из произвольных чисел. Размерность матрицы указана в Вашем варианте задания. Решение x* находится по формуле x*=A-1b. Проверить решение, то есть оценить величину |Ax*-b|
Найти произведения матриц A*A и A*A-1.
Найти скалярное произведение векторов x и b, то есть, величину 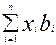
Оценить обусловленность матрицы A, то есть, найти величину 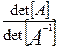 , где det[*] - определитель матрицы.
, где det[*] - определитель матрицы.
Оформить рабочий лист - то есть, выделить области ввода данных и результатов, добавить соответствующие подписи.
Таблица вариантов
| № варианта | размерность матрицы А |
| 1,3,5,7,9 | 3 строки, 3 столбца |
| 2,4,6,8,10 | 4 строки, 4 столбца |
Задание 4. Нахождение корней функции одной переменной.
Создать рабочий лист с названием " Нахождение корней ".
По аналогии с Упражнением 4 необходимо вычислить корень функции (т.е. значение х, при котором значение функции =0), указанной в Вашем варианте. Для предварительной локализации корня вначале построить график функции, по аналогии с Упражнением 3. Если вы нашли корень х=0, необходимо найти еще один корень.
Таблица вариантов
| № варианта | функция | интервал изменения аргумента х |
| 1 | y=sin3(x3+3*x) | x=-1, …1 с шагом 0.05 |
| 2 | y=sin(x)*2+1-x | x=-4, …4 с шагом 0.1 |
| 3 | y=exp(cos2(x))-2 | x=-3, …3 с шагом 0.0.5 |
| 4 | y=cos2(x)/( sin2(x+x2+2)-0.2 | x=-3, …3 с шагом 0.0.5 |
| 5 | y=sin(exp(x-1)) | x=-3, …3 с шагом 0.0.5 |
| 6 | y=tanh(sin(x)) | x=-4, …4 с шагом 0.1 |
| 7 | y=cos(1./(0.1+tanh(x))) | x=-2, …2 с шагом 0.0.5 |
| 8 | y=sin(x)-x-x.^3-x.^5-100 | x=-3, …3 с шагом 0.0.5 |
| 9 | y=sin(x)-cos(x) | x=-3, …3 с шагом 0.0.5 |
| 10 | y=sin(cosh(x)) | x=-3, …3 с шагом 0.0.5 |
Задание 5*. Задача оптимизации.
ВНИМАНИЕ!! Данное задание необходимо решить для получения оценки 5.
По аналогии с Упражнением 5 необходимо решить данную задачу оптимизации для своего варианта.
ВАРИАНТЫ
1. Завод выпускает обычные станки и станки с программным управлением, затрачивая на один обычный станок 200 кг стали и 200 кг цветного металла, а на один станок с программным управлением 700 кг стали и 100 кг цветного металла. Завод может израсходовать в месяц до 46 тонн стали и до 22 тонн цветного металла. Сколько станков каждого типа должен выпустить за месяц завод, чтобы объем реализации был максимальным, если один обычный станок стоит 2000 д.е., а станок с программным управлением 5000 д.е.
2. Для производства двух видов изделий А и В используется три типа технологического оборудования. На изготовление одного изделия А оборудование первого типа используется в течение 5 ч., второго - в течение 3 ч. и третьего - 2 ч. На производство одного изделия В, соответственно: 2 ч., 3 ч. и 3 ч. В плановом периоде оборудование первого типа может быть использовано в течение 505 ч., второго - 394 ч. и третьего - 348 ч. Прибыль от реализации одного изделия А равна 7 д.е., В - 4 д.е. Составить план производства, максимизирующий прибыль предприятия.
3. Для изготовления изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется сырья первого вида 15 кг, второго - 11 кг, третьего - 9 кг, а на производство одного изделия В, соответственно, 4 кг, 5 кг, 10 кг. Сырья первого вида имеется 1095 кг, второго - 865 кг, третьего - 1080 кг. Составить план производства, максимизирующий прибыль, если прибыль от реализации единицы изделия А составляет 3 д.е., В - 2 д.е.
4. Для производства изделий А и В используются три вида оборудования. При изготовлении одного изделия А оборудование первого вида занято 7 ч., второго - 6 ч. и третьего - 1 ч. При изготовлении одного изделия В, соответственно, 3 ч., 3 ч. и 2 ч. В месяц оборудование первого вида может быть занято 1365 ч., второго - 1245 ч. и третьего - 650 ч. Составить план производства, максимизирующий прибыль, если прибыль от реализации одного изделия А равна 6 д.е., изделия В - 5 д.е.
5. Для изготовления изделий А и В используется три вида сырья. На изготовление одного изделия А требуется 9 кг сырья первого вида, 6 кг сырья второго вида и 3 кг сырья третьего вида. На изготовление одного изделия В требуется, соответственно, 4 кг, 7 кг и 8 кг сырья. Производство обеспечено сырьем первого вида в количестве 801 кг, второго - 807 кг, третьего - 703 кг. Прибыль от продажи изделия А равна 3 д.е., изделия В - 2 д.е. Составить план производства, максимизирующий прибыль
6. Завод выпускает два вида редукторов. На изготовление одного редуктора первого вида расходуется 4 тонны чугуна и 1 тонна стали, а на изготовление одного редуктора второго вида 2 тонны чугуна и 1 тонна стали. Завод располагает на месяц 160 тоннами чугуна и 120 тоннами стали. Составить месячный план производства редукторов, максимизирующий прибыль завода, если прибыль от продажи одного редуктора первого вида равна 400 д.е., а второго - 200 д.е.
7. Для производства изделий А и В используются три вида станков. На производство одного изделия А требуется 6 ч. работы станка первого вида, 4 ч. работы станка второго вида и 3 ч. работы станка третьего вида. На производство одного изделия В требуется 2 ч. работы станка первого вида, 3 ч. работы станка второго вида и 4 ч. работы станка третьего вида. Месячный ресурс работы всех станков первого вида, имеющихся на заводе равен 600 ч., всех станков второго вида - 520 ч. и всех станков третьего вида - 600 ч. Прибыль от реализации одного изделия А равна 6 д.е., изделия В - 3 д.е. Составить план производства на месяц, максимизирующий прибыль предприятия.
8. На ферме разводят нутрий и кроликов. В недельный рацион нутрий входят 17 кг белков, 11 кг углеводов и 5 кг жиров, а для кроликов эти нормы, соответственно, равны 13 кг, 15 кг и 7 кг. Доход от реализации одного кролика 20 д.е., а от реализации одной нутрии 25 д.е. Найти план разведения животных, максимизирующий доход фермы, если ферма не может расходовать в неделю более 184 кг белков, 152 кг углеводов и 70 кг жиров.
9. Для изготовления изделий А и В предприятие использует три вида сырья. На производство одного изделия А требуется 12 кг сырья первого вида, 10 - второго и 3 - третьего, а на производство одного изделия В, соответственно, 3 кг, 5 кг, 6 кг. Производство обеспечено сырьем первого вида в количестве 684 кг, второго - 690 кг и третьего 558 кг. Одно изделие А дает предприятию 6 д.е. прибыли, изделие В - 2 д.е. Составить план производства, максимизирующий прибыль предприятия.
10. Мастерская по покраске кузовов автомобилей рассчитана на покраску не более 160 кузовов в месяц. На покраску кузова "Москвича" краски расходуется 4 кг, а кузова "Волги" - 7 кг. Мастерская располагает 820 кг краски на месяц. Составить месячный план покраски автомобилей, максимизирующий прибыль мастерской, если покраска одного "Москвича" дает 30 д.е. прибыли, а одной "Волги" - 40 д.е. прибыли.
Дата: 2019-12-10, просмотров: 550.