В процессе решения задачи для нахождения функции смешения точек натянутой струны при колебании использовались методы Фурье и конечных разностей. Методом Фурье было найдено точное решение – функция, определяющая положение любой точки струны в любой момент времени. Доказана достоверность этого решения. Приближенное решение получено методом конечных разностей в виде таблицы значений функции в узлах сетки, покрывающей область распределения, однако оно дает большую погрешность.
Исследование волнового процесса проводилось табулированием функции, найденной методом Фурье. В качестве материалов стержня в различных случаях использовались железо и алюминий, в качестве среды колебания – вода и машинное масло. Затухание процесса в железной струне произошло приблизительно на 60 и 3.5 секунде, в алюминиевой – на 20 и 6 секундах для воды, и машинного масла соответственно. Таким образом, численно доказано, что время затухания процесса колебания струны зависит от используемого материала и среды, в которой проводится процесс. Причем, длительность процесса зависит не только от упругих свойств материала струны и вязкости среды, но и от плотности самого материала струны, так как она влияет на коэффициент сопротивления среды.
Изначально оба конца струны зафиксированы в точках 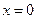 ,
, 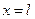 , а сама функция имеет вид прямой. Затем точке с на струне сообщают начальную скорость ударом молоточка, она начинает совершать колебательные движения, причем значение ее максимального отклонения в точке удара постепенно убывает и через некоторый промежуток времени становится близким к нулю. Продолжительность колебаний тем больше, чем ближе к середине струны находится точка удара с.
, а сама функция имеет вид прямой. Затем точке с на струне сообщают начальную скорость ударом молоточка, она начинает совершать колебательные движения, причем значение ее максимального отклонения в точке удара постепенно убывает и через некоторый промежуток времени становится близким к нулю. Продолжительность колебаний тем больше, чем ближе к середине струны находится точка удара с.
Поведение функции объясняет физический смысл задачи: волновой процесс затухает тем быстрее, чем сильнее вязкость среды и чем меньше упругие свойства материала струны.
Список использованной литературы и пакетов прикладных программ.
1. Mathematica 5 © Copyright 1988-2003 Wolfram Research, Inc.
2. Араманович И.Г., Левин В.И. Уравнения математической физики: Учеб. для втузов: - М. : Издательство Наука, 1969. – 288 с.
3. Евграфова Н.Н., Каган. В.Л. Курс физики: Учеб пособие для подготовительных отделения вузов -. 2-е изд. –М.: Высш. школа, 1978 .- 512 с.
4. Чертов А.Г., Воробьев А.А. Задачник по физике: Учеб пособие для втузов .- 7-е изд., перераб. и доп. –М.: Издательство Физико-математической литературы, 2001 .- 640с.
5. Уравнения математической физики © Copyright 2005 Голубев В.О.
Приложение 1. Графики функций отклонения струны и скорости колебания.
Управляемые параметры 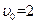 ,
, 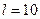 ,
, 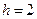 ,
, 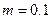 ,
, 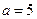 ,
, 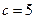 ,
, 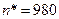 ::
::
Интервалы изменения переменных 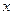 и
и 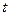 :
: 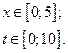
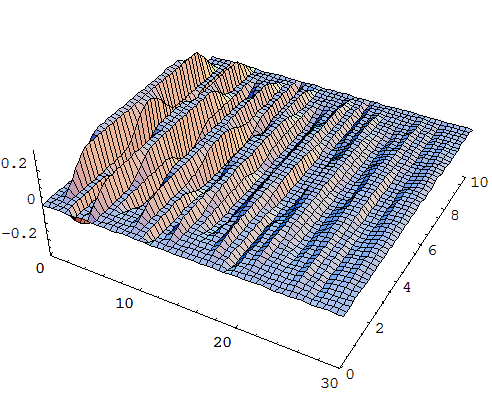
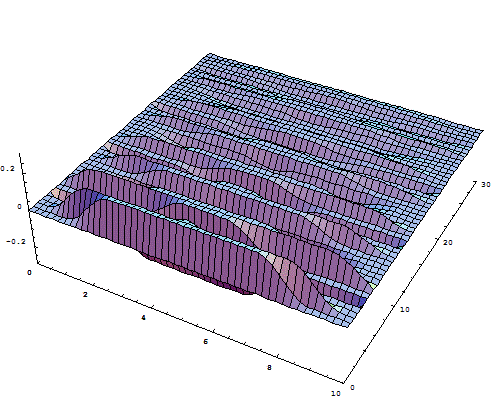
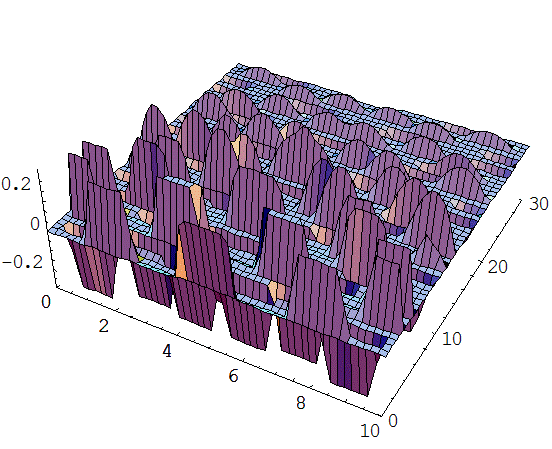
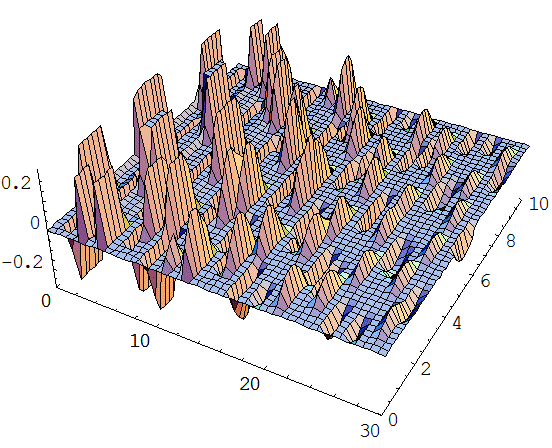
Приложение 2. Графики функций отклонения струны из различных материалов в различных средах.
Случай вода – железо:
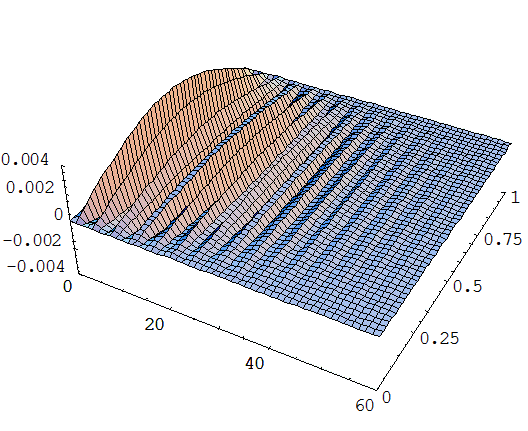
Случай вода – алюминий:
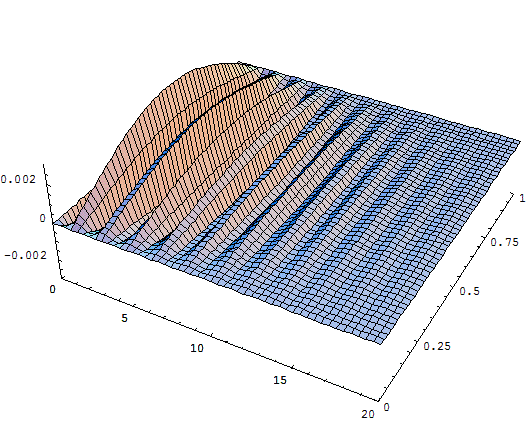
Случай машинное масло – железо:
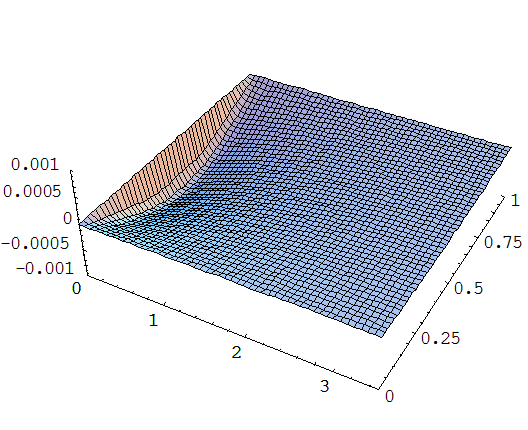
Случай машинное масло – алюминий:
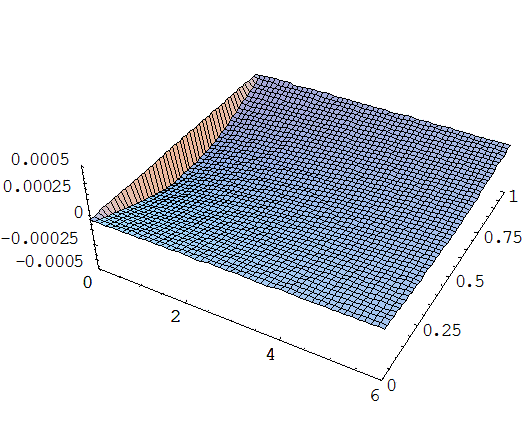
Дата: 2019-12-10, просмотров: 349.