Функцию 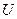 будем искать в виде будем искать в виде 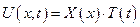
| (1) |
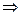
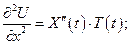
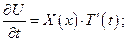
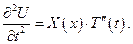
Тогда ДУЧП принимает вид: 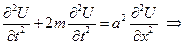
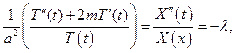
 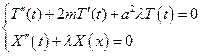
| (2) |
где 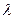 - это постоянная и по х, и по t.
- это постоянная и по х, и по t.
Таким образом, ДУЧП заменилось на два обыкновенных ДУ относительно функций 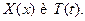
При этих действиях 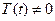 и
и 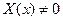 , так как в противном случае
, так как в противном случае 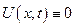 , что не удовлетворяет начальным условиям.
, что не удовлетворяет начальным условиям.
Переносим теперь нулевые граничные условия на одну из функций в равенстве (1):
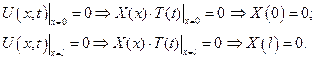
Сформулируем задачу Штурма–Лиувилля: найти значения 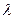 , при которых существуют нетривиальные решения системы
, при которых существуют нетривиальные решения системы
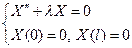
| (3) |
Найти собственные функции 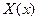 , соответствующие собственным числам
, соответствующие собственным числам  .
.
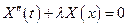 - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общим решением уравнения является функция
- линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Общим решением уравнения является функция 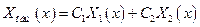 , где
, где 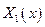 и
и 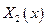 - фундаментальная система частных решений, которая находится через характеристическое уравнение:
- фундаментальная система частных решений, которая находится через характеристическое уравнение:
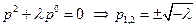 .
.
Рассмотрим 3 случая для значений  , приводящих к различным корням характеристическое уравнение :
, приводящих к различным корням характеристическое уравнение :
1) 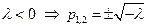 - действительные противоположные по знаку корни
- действительные противоположные по знаку корни
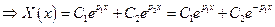 - общее решение;
- общее решение;
удовлетворяем нулевым граничным условиям:
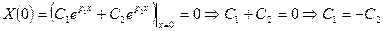 ;
;
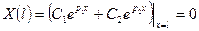
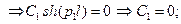
так как 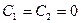 , то
, то 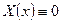 - только тривиальное решение.
- только тривиальное решение.
Задача Штурма-Лиувилля неразрешима при 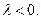
2) 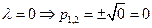 - равные действительные корни
- равные действительные корни
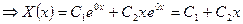 - общее решение;
- общее решение;
удовлетворяем нулевым граничным условиям:
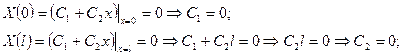
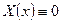 - только тривиальное решение. Задача Штурма-Лиувилля неразрешима при
- только тривиальное решение. Задача Штурма-Лиувилля неразрешима при 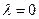 .
.
3) 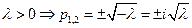 - комплексно-сопряженные корни
- комплексно-сопряженные корни
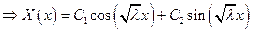 - общее решение;
- общее решение;
удовлетворяем нулевым граничным условиям:
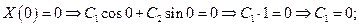
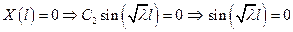
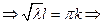
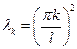 , , 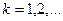
| (4) |
Это собственные числа задачи Штурма – Лиувилля.
Соответствующие им собственные функции: 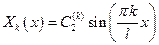 . .
| (5) |
Решим теперь второе уравнение системы (2) при 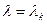 :
:
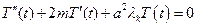 - линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. общим решением уравнения будет функция
- линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами. общим решением уравнения будет функция 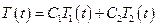 , где
, где 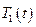 и
и 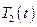 - фундаментальная система частных решений, которая находится через характеристическое уравнение:
- фундаментальная система частных решений, которая находится через характеристическое уравнение:
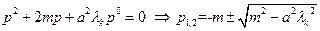 .
.
Мы будем предполагать, что коэффициент m настолько мал, что подкоренное выражение отрицательно для любых значений 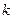 . Ясно, что это будет тогда, когда
. Ясно, что это будет тогда, когда 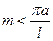 . Вводя обозначение
. Вводя обозначение 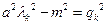 , получим
, получим 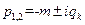 . Следовательно, общее решение уравнения таково:
. Следовательно, общее решение уравнения таково:
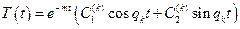 , ,
| (6) |
где 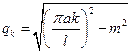 , , 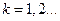
| (7) |
Перемножим 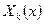 и
и 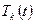 и получим последовательность функций
и получим последовательность функций 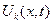 :
:
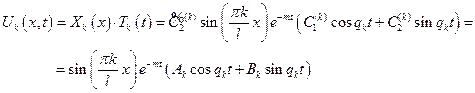
где 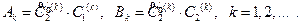
Каждая из этих функций удовлетворяет исходному уравнению 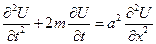 и нулевым граничным условиям, следовательно ряд из этих функций будет удовлетворять этому уравнению и нулевым граничным условиям:
и нулевым граничным условиям, следовательно ряд из этих функций будет удовлетворять этому уравнению и нулевым граничным условиям:
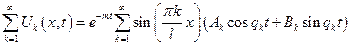
| (8) |
Коэффициенты 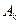 и
и 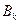 можно найти, удовлетворяя функцию начальным условиям:
можно найти, удовлетворяя функцию начальным условиям:
1) 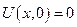
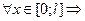
 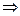 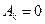 . .
| (9) |
2) 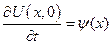
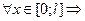
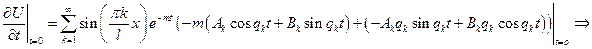
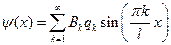 , так как
, так как 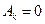 .
.
Таким образом, получено представление 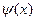 тригонометрическим рядом Фурье с разложением по синусам. Тогда коэффициенты
тригонометрическим рядом Фурье с разложением по синусам. Тогда коэффициенты 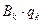 можно определить по формулам Фурье.
можно определить по формулам Фурье.
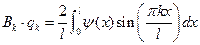
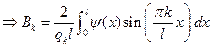
| (10) |
Так как функция 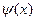 равна 0 при
равна 0 при 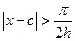 , то интегрирование можно вести только по промежутку
, то интегрирование можно вести только по промежутку 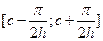 :
:
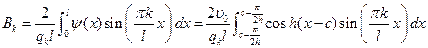 .
.
Вычислим сначала неопределенный круговой интеграл:
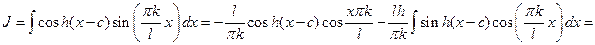
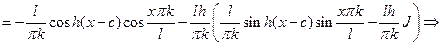
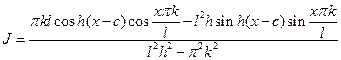 ;
;
в подстановке имеем:
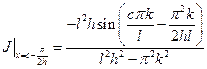 ,
, 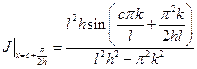 .
.
Окончательно, 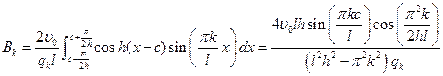 .
.
Наконец, функция 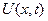 принимает вид:
принимает вид:
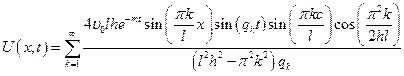 ,
, 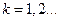 ,
,
где 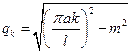 .
.
Дата: 2019-12-10, просмотров: 338.