Подставим функцию в исходное дифференциальное уравнение 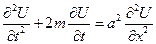 .
.
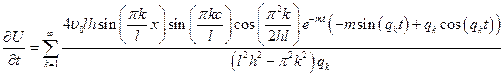
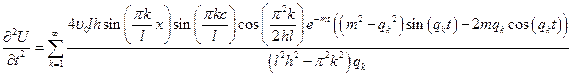
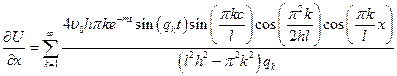
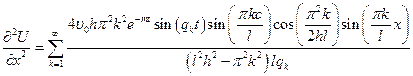
Перенесем 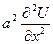 в левую часть:
в левую часть:
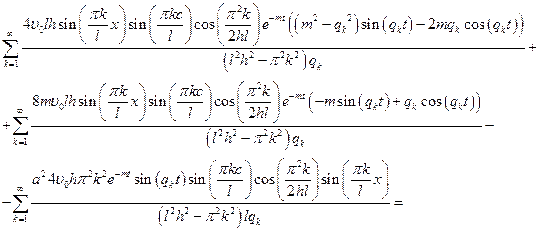
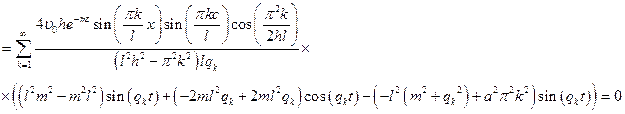 Очевидно, что выражение в скобках дает 0. Следовательно, найденная функция удовлетворяет ДУЧП.
Очевидно, что выражение в скобках дает 0. Следовательно, найденная функция удовлетворяет ДУЧП.
Проверим, удовлетворяет ли функция начальным и граничным условиям.
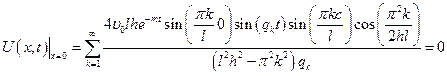 ;
;
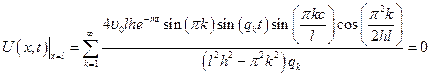 ;
;
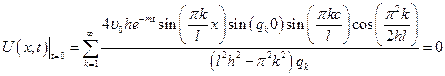 ;
;
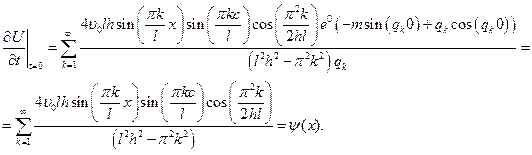
 найденная функция удовлетворяет всем начальным и граничным условиям.
найденная функция удовлетворяет всем начальным и граничным условиям.
Теперь подберем такое количество членов ряда 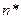 , чтобы равенство
, чтобы равенство 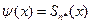 , удовлетворялось с точностью до 10-5 при
, удовлетворялось с точностью до 10-5 при 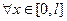 . Результат подбора при
. Результат подбора при 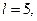
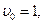
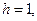
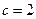 -
- 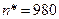 :
:
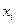
| 0 | 0.1 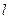
| 0.2 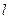
| 0.3 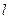
| 0.4 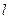
| 0.5 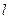
| 0.6 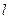
| 0.7 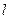
| 0.8 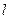
| 0.9 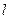
| 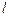
|
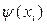
| 0 | 0.07074 | 0.5403 | 0.87758 | 1 | 0.87758 | 0.54030 | 0.07073 | 0 | 0 | 0 |
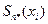
| 0 | 0.07074 | 0.5403 | 0.87758 | 1 | 0.87758 | 0.54030 | 0.07073 | 0 | 0 | 0 |
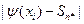
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
График функции 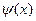 График разложения
График разложения  в ряд Фурье при
в ряд Фурье при 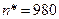
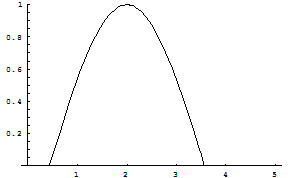
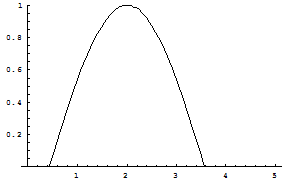
Достоверность решения доказана.
Вывод конечно-разностных уравнений, формулировка вычислительной схемы метода конечных разностей
При решении уравнений с частными производными методом конечных разностей производные заменяются соответствующими разностями применяем 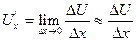 .
.
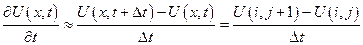 (1)
(1)
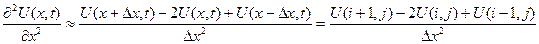 (2)
(2)
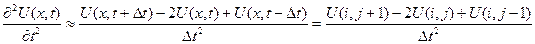 (3)
(3)
Краевая задача для волнового уравнения:
 требуется найти решения уравнения
требуется найти решения уравнения 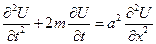 , удовлетворяющие краевым условиям:
, удовлетворяющие краевым условиям:
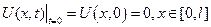 ,
,
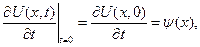
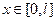 ,
,
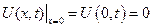 ,
, 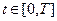
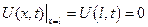 ,
, 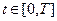 .
.
то есть требуется найти решение 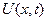 в прямоугольнике, ограниченном прямыми
в прямоугольнике, ограниченном прямыми 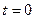 ,
, 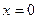 ,
, 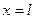 ,
, 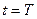 , если заданы значения искомой функции на трех его сторонах
, если заданы значения искомой функции на трех его сторонах 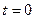 ,
, 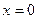 ,
, 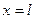 и значение производной при
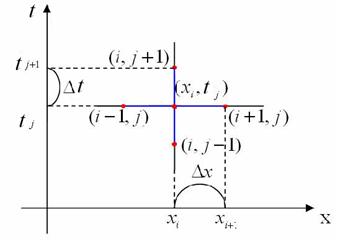
и значение производной при 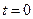 . Покроем нашу область сеткой, образованной прямыми
. Покроем нашу область сеткой, образованной прямыми
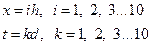
и будем определять приближенные значения в узлах сетки, т. е. в точках пересечения этих прямых. Введем обозначения: 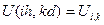 . Напишем вместо волнового уравнения соответствующее ему уравнение в конечных разностях для точки
. Напишем вместо волнового уравнения соответствующее ему уравнение в конечных разностях для точки 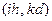 . В соответствии с формулами (1), (2) и (3) получим
. В соответствии с формулами (1), (2) и (3) получим
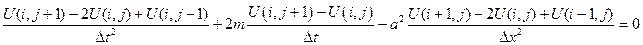
В итоге получим систему из 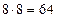 уравнений, решения которой являются приближенными значениями функции в узлах сетки разбиения:
уравнений, решения которой являются приближенными значениями функции в узлах сетки разбиения:
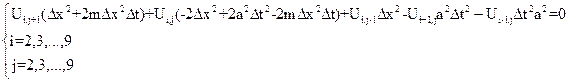
Табулирование значений искомой функции в узлах сетки, покрывающей область, в которой найдено решение. Построение графика найденной функции.
Таблица точных значений функции при следующих значениях управляющих параметров: 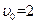 ,
, 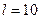 ,
, 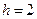 ,
, 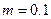 ,
, 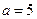 ,
, 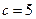 ,
, 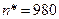 :
:
| t\x | 0.00000 | 1.00000 | 2.00000 | 3.00000 | 4.00000 | 5.00000 | 6.00000 | 7.00000 | 8.00000 | 9.00000 | 10.00000 |
| 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 1.50000 | 0.00000 | 0.00034 | 0.01433 | 0.15939 | 0.17309 | 0.17311 | 0.17309 | 0.15939 | 0.01433 | 0.00034 | -0.00000 |
| 3.00000 | 0.00000 | -0.14829 | -0.14839 | -0.14847 | -0.14851 | -0.14853 | -0.14851 | -0.14847 | -0.14839 | -0.14829 | -0.00000 |
| 4.50000 | 0.00000 | -0.00051 | 0.00908 | 0.11616 | 0.12630 | 0.12631 | 0.12630 | 0.11616 | 0.00908 | -0.00051 | -0.00000 |
| 6.00000 | 0.00000 | 0.00066 | 0.00132 | 0.00198 | 0.00264 | 0.00311 | 0.00264 | 0.00198 | 0.00132 | 0.00066 | 0.00000 |
| 7.50000 | 0.00000 | -0.00075 | -0.00899 | -0.08887 | -0.09639 | -0.09640 | -0.09639 | -0.08887 | -0.00899 | -0.00075 | 0.00000 |
| 9.00000 | 0.00000 | 0.08137 | 0.08142 | 0.08145 | 0.08147 | 0.08148 | 0.08147 | 0.08145 | 0.08142 | 0.08137 | 0.00000 |
| 10.50000 | 0.00000 | 0.00071 | -0.00413 | -0.06268 | -0.06823 | -0.06824 | -0.06823 | -0.06268 | -0.00413 | 0.00071 | 0.00000 |
| 12.00000 | 0.00000 | -0.00073 | -0.00145 | -0.00218 | -0.00290 | -0.00342 | -0.00290 | -0.00218 | -0.00145 | -0.00073 | -0.00000 |
| 13.50000 | 0.00000 | 0.00072 | 0.00554 | 0.04953 | 0.05365 | 0.05366 | 0.05365 | 0.04953 | 0.00554 | 0.00072 | -0.00000 |
| 15.00000 | 0.00000 | -0.04464 | -0.04466 | -0.04467 | -0.04467 | -0.04467 | -0.04467 | -0.04467 | -0.04466 | -0.04464 | -0.00000 |
| 16.50000 | 0.00000 | -0.00063 | 0.00179 | 0.03380 | 0.03684 | 0.03684 | 0.03684 | 0.03380 | 0.00179 | -0.00063 | -0.00000 |
| 18.00000 | 0.00000 | 0.00060 | 0.00119 | 0.00179 | 0.00239 | 0.00281 | 0.00239 | 0.00179 | 0.00119 | 0.00060 | 0.00000 |
| 19.50000 | 0.00000 | -0.00056 | -0.00336 | -0.02759 | -0.02985 | -0.02985 | -0.02985 | -0.02759 | -0.00336 | -0.00056 | 0.00000 |
| 21.00000 | 0.00000 | 0.02449 | 0.02449 | 0.02449 | 0.02449 | 0.02448 | 0.02449 | 0.02449 | 0.02449 | 0.02449 | 0.00000 |
| 22.50000 | 0.00000 | 0.00048 | -0.00072 | -0.01822 | -0.01988 | -0.01988 | -0.01988 | -0.01822 | -0.00072 | 0.00048 | 0.00000 |
| 24.00000 | 0.00000 | -0.00044 | -0.00087 | -0.00131 | -0.00175 | -0.00206 | -0.00175 | -0.00131 | -0.00087 | -0.00044 | -0.00000 |
| 25.50000 | 0.00000 | 0.00039 | 0.00202 | 0.01536 | 0.01660 | 0.01660 | 0.01660 | 0.01536 | 0.00202 | 0.00039 | -0.00000 |
| 27.00000 | 0.00000 | -0.01343 | -0.01342 | -0.01342 | -0.01341 | -0.01341 | -0.01341 | -0.01342 | -0.01342 | -0.01343 | -0.00000 |
| 28.50000 | 0.00000 | -0.00034 | 0.00025 | 0.00981 | 0.01072 | 0.01072 | 0.01072 | 0.00981 | 0.00025 | -0.00034 | -0.00000 |
| 30.00000 | 0.00000 | 0.00030 | 0.00060 | 0.00090 | 0.00120 | 0.00141 | 0.00120 | 0.00090 | 0.00060 | 0.00030 | 0.00000 |
Таблица приближенных значений функции при следующих значениях управляющих параметров: 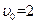 ,
, 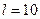 ,
, 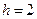 ,
, 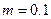 ,
, 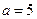 ,
, 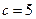 ,
, 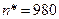 :
:
| t\x | 0.00000 | 1.00000 | 2.00000 | 3.00000 | 4.00000 | 5.00000 | 6.00000 | 7.00000 | 8.00000 | 9.00000 | 10.00000 |
| 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 1.50000 | 0.00000 | 0.01054 | 0.01644 | 0.18001 | 0.21407 | 0.22213 | 0.21407 | 0.18001 | 0.01644 | 0.01054 | -0.00000 |
| 3.00000 | 0.00000 | -0.13629 | -0.12855 | -0.11852 | -0.10851 | -0.10681 | -0.10851 | -0.11852 | -0.12855 | -0.13629 | -0.00000 |
| 4.50000 | 0.00000 | 0.01001 | 0.02808 | 0.14679 | 0.16673 | 0.16671 | 0.16673 | 0.14679 | 0.02808 | 0.01001 | -0.00000 |
| 6.00000 | 0.00000 | -0.01055 | 0.01252 | 0.03100 | 0.00500 | 0.04365 | 0.00500 | 0.03100 | 0.01252 | -0.01055 | 0.00000 |
| 7.50000 | 0.00000 | 0.01033 | 0.01113 | -0.05924 | -0.06639 | -0.05740 | -0.06639 | -0.05924 | 0.01113 | 0.01033 | 0.00000 |
| 9.00000 | 0.00000 | 0.08137 | 0.09282 | 0.11153 | 0.11150 | 0.12187 | 0.11150 | 0.11153 | 0.09282 | 0.08137 | 0.00000 |
| 10.50000 | 0.00000 | 0.00071 | 0.01406 | -0.03270 | -0.03877 | -0.03723 | -0.03877 | -0.03270 | 0.01406 | 0.00071 | 0.00000 |
| 12.00000 | 0.00000 | -0.00073 | -0.00145 | 0.03009 | 0.03259 | 0.02200 | 0.03259 | 0.03009 | -0.00145 | -0.00073 | -0.00000 |
| 13.50000 | 0.00000 | 0.00072 | 0.00554 | 0.06903 | 0.07345 | 0.08366 | 0.07345 | 0.06903 | 0.00554 | 0.00072 | -0.00000 |
| 15.00000 | 0.00000 | -0.04464 | -0.04466 | -0.02567 | -0.02477 | -0.01467 | -0.02477 | -0.02567 | -0.04466 | -0.04464 | -0.00000 |
| 16.50000 | 0.00000 | -0.00063 | 0.00179 | 0.05387 | 0.05690 | 0.05665 | 0.05690 | 0.05387 | 0.00179 | -0.00063 | -0.00000 |
| 18.00000 | 0.00000 | 0.00060 | 0.00119 | 0.02179 | 0.02245 | 0.02287 | 0.02245 | 0.02179 | 0.00119 | 0.00060 | 0.00000 |
| 19.50000 | 0.00000 | -0.00056 | -0.00336 | -0.01759 | -0.00785 | -0.00085 | -0.00785 | -0.01759 | -0.00336 | -0.00056 | 0.00000 |
| 21.00000 | 0.00000 | 0.02449 | 0.02449 | 0.01450 | 0.04749 | 0.04450 | 0.04749 | 0.01450 | 0.02449 | 0.02449 | 0.00000 |
| 22.50000 | 0.00000 | 0.00048 | -0.00072 | -0.01822 | -0.01988 | -0.00988 | -0.01988 | -0.01822 | -0.00072 | 0.00048 | 0.00000 |
| 24.00000 | 0.00000 | -0.00044 | -0.00087 | -0.00131 | -0.00175 | 0.01308 | -0.00175 | -0.00131 | -0.00087 | -0.00044 | -0.00000 |
| 25.50000 | 0.00000 | 0.00039 | 0.00202 | 0.01536 | 0.01660 | 0.02060 | 0.01660 | 0.01536 | 0.00202 | 0.00039 | -0.00000 |
| 27.00000 | 0.00000 | -0.01343 | -0.01342 | -0.01342 | -0.01341 | -0.01350 | -0.01341 | -0.01342 | -0.01342 | -0.01343 | -0.00000 |
| 28.50000 | 0.00000 | -0.00034 | 0.00025 | 0.00981 | 0.01072 | 0.01080 | 0.01072 | 0.00981 | 0.00025 | -0.00034 | -0.00000 |
| 30.00000 | 0.00000 | 0.00030 | 0.00060 | 0.00090 | 0.00120 | 0.00149 | 0.00120 | 0.00090 | 0.00060 | 0.00030 | 0.00000 |
Как видно из представленных таблиц табуляции относительная погрешность между точными и приближёнными значениями функции достигает 30%. Это говорит о том, что конечно-разностный метод дает плохую сходимость для волнового уравнения. График найденной функции при вышеуказанных параметрах в области 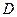 приведен в приложении.
приведен в приложении.
Дата: 2019-12-10, просмотров: 308.