Смесь, состоящая из двух и более компонентов, характеризуется свойствами и содержанием этих компонентов. Состав смеси может быть задан массой, объемом, количеством (числом молей или килограмм-молей) отдельных компонентов, а также значениями их концентраций. Концентрацию компонента в смеси можно выразить в весовых, мольных и объемных долях или процентах, а также в других единицах.
Массовая доля wi какого-либо компонента определяется отношением массы mi данного компонента к массе всей смеси mсм:
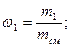
Учитывая, что суммарная масса смеси равна сумме масс отдельных компонентов, т.е.
можно написать:
или сокращенно:
Пример 4.Смесь состоит из двух компонентов: m1 = 500 кг, m2 = 1500 кг. Определить массовую долю каждого компонента в смеси.
Решение. Массовая доля первого компонента:
mсм= m1 + m2 = 500 + 1500 = 2000 кг
Массовая доля второго компонента:
Массовую долю второго компонента можно определить также, используя равенство:
w1 + w2 = 1
w2 = 1 – w1 = 1 – 0,25 = 0,75
Объемная доляni компонента в смеси равна отношению объема Vi данного компонента к объему всей смеси V:
Учитывая, что:
можно написать:
Пример 5. Газ состоит из двух компонентов: V1 = 15,2 м3 метана и V2 = 9,8 м3 этана. Подсчитать объемный состав смеси.
Решение. Общий объем смеси равен:
V = V1 + V2 = 15,2 + 9,8 = 25 м3
Объемная доля в смеси:
метана 
этана v2 = 1 – v1 = 1 – 0,60 = 0,40
Мольная доляni какого-либо компонента смеси определяется как отношение числа киломолей Ni данного компонента к общему числу киломолей N смеси:
Учитывая, что: 
получим: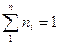 
Пересчет мольных долей в массовые можно проводить по формуле:
Пример 6. Смесь состоит из 500 кг бензола и 250 кг толуола. Определить мольный состав смеси.
Решение. Молекулярный вес бензола (С6Н6) равен 78, толуола (С7Н8) – 92. Число килограмм-молей равно:
бензола 
толуола 
общее число килограмм-молей:
N = N1 + N2 = 6,41 + 2,72 = 9,13
Мольная доля бензола равна:
Для толуола мольная доля может быть найдена из равенства:
n1 + n2 = 1
откуда: n2 = 1 – n1 = 1 – 0,70 = 0,30
Среднюю молекулярную массу смеси можно определить, зная мольную долю и молекулярную массу каждого компонента смеси:
(21)
где ni — содержание компонентов в смеси, мол. доли; Mi — молекулярная масса компонента смеси.
Молекулярную массу смеси нескольких нефтяных фракций можно определить по формуле
(22)
или
(23)
где m1, m2,…, mn — масса компонентов смеси, кг; M1, М2,....,.Мп - молекулярная масса компонентов смеси; 
- % масс. компонента.
Молекулярную массу нефтепродукта можно определить также по формуле Крэга
(24)
Пример 7. Определить среднюю молекулярную массу смеси бензола с изооктаном, если мольная доля бензола составляет 0,51, изооктана 0,49.
Решение. Молекулярная масса бензола 78, изооктана 114. Подставляя эти значения в формулу (21), получаем
Мср = 0,51 × 78 + 0,48×114 = 95,7
Пример 8. Смесь состоит из 1500кг бензола и 2500кг н-октана. Определить среднюю молекулярную массу смеси.
Решение. Используем формулу (22)
Объемный молярный состав пересчитывают в массовый следующим образом. Данный объемный (молярный) состав в процентах принимают за 100 молей. Тогда концентрация каждого компонента в процентах будет выражать число его молей. Затем число молей каждого компонента умножают на его молекулярную массу и получают массу каждого компонента в смеси. Разделив массу каждого компонента на общую массу, получают его массовую концентрацию.
Массовый состав пересчитывают в объемный (молярный) следующим образом. Принимают, что смеси взято 100 (г, кг, т) (если массовый состав выражен в процентах), массу каждого компонента делят на его молекулярную массу. Получают число молей. Делением числа молей каждого компонента на их общее число получают объемные (молярные) концентрации каждого компонента.
Средняя плотность газа определяется по формуле:
кг/м3; г/см3
или, исходя из объемного состава:
,
или, исходя из массового состава смеси:
.
Относительную плотность определяют по формуле:
Пример 9. Пересчитать массовый состав газа в объемный и определить его молекулярную массу, его плотность и относительную плотность.
| Компоненты | М г/моль | массовый состав, % масс. | mi | Число молей
 
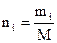
| Объемный состав | |
| доли единицы | % об. | |||||
| Метан | 40:16=2,50 | 0,669 | 66,9 | |||
| Этан | 10:30=0,33 | 0,088 | 8,8 | |||
| Пропан | 15:44=0,34 | 0,091 | 9,1 | |||
| Бутан | 25:58=0,43 | 0,115 | 11,5 | |||
| Пентан + высшие | 10:72=0,14 | 0,037 | 3,7 | |||
| 3,74 | 1,000 | 100,0 |
Для простоты расчета примем массу смеси за 100 г, тогда масса каждого компонента будет численно совпадать с процентным составом. Найдем число молей ni каждого компонента. Для этого массу каждого компонента mi разделим на мольную массу:
Находим объемный состав смеси в долях единицы
wi(CH4) = 2,50 : 3,74 = 0,669; w(C2H6) = 0,33 : 3,74 = 0,088;
w(C5H8) = 0,34 : 3,74 = 0,091; w(C4H10) = 0,43 : 3,74 = 0,115;
w(C5H12) = 0,14 : 3,74 = 0,037.
Находим объемный состав смеси в процентах, умножив данные в долях единицы на 100%. Все полученные данные заносим в таблицу.
Рассчитываем среднюю массу смеси.
Мср = 100 : 3,74 = 26,8 г/моль
Находим плотность смеси 
Находим относительную плотность:
Пример 10. Пересчитать объемный состав в массовый и определить его молекулярную массу, его плотность и относительную плотность.
| Компоненты | М г/моль | Объемный состав, % об. | число молей ni | Масса компонента г. | Весовой состав | |
| доли единицы | % масс. | |||||
| Метан | 30×16=480 | 0,117 | 11,7 | |||
| Этан | 15·30=450 | 0,109 | 10,9 | |||
| Пропан | 20·44=880 | 0,214 | 21,4 | |||
| Бутан | 15·58=870 | 0,211 | 21,1 | |||
| Пентан + высшие | 20·72=1440 | 0,349 | 34,9 | |||
| 1,000 | 100,0 |
w(CH4) = 480 : 4120 = 0,117; w(C2H6) = 450 : 4120 = 0,109;
w(C3H8) = 880 : 4120 = 0,214; w(C4H10) = 870 : 4120 = 0,211;
w(C5H12) = 1440 : 4120 = 0,349.
Мср = 4120 : 100 = 41,2 г/моль.
г/л
Задача 15. Смесь состоит из пяти компонентов. Определить массовую, объемную и мольную долю каждого компонента в смеси, среднюю молекулярную массу смеси.
| Компоненты смеси | Вариант | |||||||||
| mi (г) | mi (кг) | mi (т) | ||||||||
| метан | ||||||||||
| этан | ||||||||||
| пропан | ||||||||||
| н-бутан | ||||||||||
| изобутан |
Задача 16. Пересчитать массовый состав газа в объемный и определить его молекулярную массу, плотность и относительную плотность по воздуху.
| Компоненты смеси | ω% массовый состав газа | |||||||||
| Варианты | ||||||||||
| метан | ||||||||||
| этан | ||||||||||
| пропан | ||||||||||
| бутан | ||||||||||
| пентан |
Задача 17. Пересчитать объемный состав газа в массовый и определить его молекулярную массу, плотность и относительную плотность по воздуху.
| Компоненты смеси | объемный состав газа ω% объем | |||||||||
| Варианты | ||||||||||
| метан | ||||||||||
| этан | ||||||||||
| пропан | ||||||||||
| бутан | ||||||||||
| пентан |
Давление насыщенных паров
Давление насыщенных паров - это давление, производимое паровой фазой, которая находится в равновесии с жидкостью при определенной температуре. Давление насыщенных паров индивидуального чистого вещества зависит только от температуры. Для смесей и таких продуктов, как нефть и нефтепродукты, давление насыщенных паров зависит не только от температуры, но и от состава паровой и жидкой фаз и их соотношения. Поэтому определение давления насыщенных паров нефтепродуктов представляет большие трудности. Однако для узких нефтяных фракций, выкипающих в узком интервале температур без заметного изменения состава фаз, можно с известной степенью приближения считать однозначной зависимость давления насыщенных паров от температуры. Единица давления в системе единиц СИ - паскаль (Па). Кратные единицы кПа, МПа. Паскаль - давление, вызываемое силой 1 ньютон (Н), равномерно распределенной по поверхности площадью 1м2 и нормально к ней направленной.
При изучении фракционного состава нефтей и проведении технологических расчетов аппаратуры приходится пересчитывать давление насыщенных паров нефтепродуктов при одной температуре на давление при другой, а также температуру кипения нефтяных фракций от одного давления к другому. Для осуществления таких пересчетов предложены формулы и номограммы (Приложения 7 и 8).
Пример 11. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 149°С. Какова температура кипения этой фракции при 266,6 кПа?
Решение. По графику (Приложение 7) на оси координат находят точку, соответствующую температуре 149°С, и из этой точки проводят прямую, параллельную оси абсцисс, до пересечения с вертикальной линией, отвечающей давлению 101,3 кПа. Получают точку А, которая легла на искомый луч. Затем от точки, соответствующей давлению 266,6 кПа, проводят вертикаль до пересечения с найденным лучом в точке В. Из точки В проводят горизонтальную линию, параллельную оси абсцисс, до пересечения со шкалой температур в точке С. Эта точка дает значение искомой температуры кипения, равной 190°С.
Пример 12. При разгонке мазута из колбы Кляйзена температура паров в момент замера была равна 150°С, а остаточное давление 0,266 кПа. Какова температура паров при атмосферном давлении?
Решение. Используют номограмму (Приложение 8). На левой шкале номограммы отмечают температуру 150°С, на правой шкале - давление 0,266 кПа. Эти точки соединяют прямой, и в точке пересечения со шкалой «температура кипения при нормальном давлении» находят значение искомой температуры, равной 330°С.
Для подсчета давления насыщенных паров узких нефтяных фракций при низких давлениях пользуются формулой Ашворта
(25)
где Р - давление насыщенных паров, Па; Т - соответствующая температура, К; То - температура кипения фракции при атмосферном давлении, К; f(T) - функция температуры Т, выражаемая уравнением
(26)
Функцию f(T0) определяют аналогично. Значения функции для различных температур (Т и Т0) приведены в Приложении 9.
Пример 13. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения 170°С. Определить давление насыщенных паров этой фракции при 260°С.
Решение. Для решения задачи используем формулу Ашворта (25).
По Приложению 9 найдем значения f(T0) для температуры 170°С и f(T) для температуры 260°С
f(T0) = 4,124 f(T) = 2,924
Подставим эти величины в формулу (25)
По таблицам антилогарифмов находим значение этого числа и получим
Р - 3158 = 590 900
Р = 590 900 + 3158 = 594 058 Па
Давление насыщенных паров данной фракции при 260°С
Р = 594 058 Па
На давление насыщенных паров оказывает влияние фракционный состав, отношения объемов паров и жидкости в рабочем баллоне, температура. При низких температурах и температурах, близких к начальной температуре кипения фракции, формула Ашворта дает несколько заниженные значения давления насыщенных паров.
Для определения давления насыщенных паров светлых нефтепродуктов и их узких фракций предложена формула
, кПа (27)
где
Для товарных бензинов 
= 1,5 - 2,5.
Эта формула дает возможность определить давление насыщенных паров светлых нефтепродуктов, используя характерные температуры кипения.
Задача 18. Узкая нефтяная фракция при давлении Р0 имеет среднюю температуру кипения t0 0С. Какова температура кипения этой фракции при Р1 кПа?
| параметры | вариант | |||||||||
| t0 0С | ||||||||||
| Р0 кПа | 103 | 103 | 103 | 104 | 104 | 105 | 105 | 106 | 106 | 107 |
| Р1 кПа | 104 | 5×103 | 5×103 | 105 | 106 | 106 | 106 | 105 | 105 | 105 |
Задача 19. При разгонке нефтепродукта температура паров в момент замера была равна t0 0С, а остаточное давление Р0 кПа. Какова температура паров при атмосферном давлении?
| параметры | вариант | |||||||||
| t0 0С | ||||||||||
| Р0 кПа | 0,2 | 0,01 | 0,6 |
Задача 20. Узкая нефтяная фракция при атмосферном давлении имеет среднюю температуру кипения t0 0С. Определить давление насыщенных паров этой фракции при t1 0С.
| параметры | вариант | |||||||||
| t0 0С | ||||||||||
| t1 0С |
Дата: 2016-10-02, просмотров: 516.
