Показатели асимметрии и эксцесса.Распределение частот в изучаемом объекте не всегда подчиняется закону нормального распределения. Это особенно четко проявляется при выражении вариационного ряда в виде графика. Распределение частот может быть представлено асимметричной, островершинной или туповершинной кривой.
Асимметрия кривой распределения обусловлена неравномерным размещением вариант по обе стороны от модального значения признака. Если число вариант больше справа от моды, распределение имеет положительную асимметрию, если слева – отрицательную (рис. 1.2).
Рис. 1.2. Асимметричное распределение:
а – отрицательная асимметрия, б – положительная асимметрия
При получении асимметричной кривой следует проверить асимметричность распределения. Если асимметричность не будет доказана по критерию Стьюдента, то рассматриваемое распределение относят к симметричному. Для проверки асимметричности распределения вычисляют коэффициент асимметрии, его ошибку, затем на основании показателя достоверности устанавливают вид кривой распределения. Коэффициент асимметрии находят:
Kas = (M – Mo) / σ, или Kas = (M – Me) / σ.
Пример. При изучении содержания подвижного бора в дерново-подзолистых почвах были получены следующие показатели: М = 0,25 мг/кг, Мо = 0,28, σ = 0,02, N = 20. Для получения представления о форме кривой распределения бора предварительно вычисляем коэффициент асимметрии:
Кas = (0,25 – 0,28) / 0,02 = –1,5.
Полученная величина указывает на наличие отрицательной асимметрии в распределении вариант содержания подвижного бора в дерново-подзолистых почвах. Затем находим ошибку коэффициента асимметрии:
mas = 1= 
) = 0,51.
Достоверность коэффициента асимметрии определяется по критерию Стъюдента: t = Kas / mas = –1,5 / 0,51 = –2,94.
Величина критерия Стьюдента (см. прил. 4) для Р0,99при ν→∞ составляет 2,58 (число степеней свободы принимается равным бесконечности). Рассчитанный критерий Стьюдента (2,94) больше табличного для Р0,99 (2,58), что указывает на асимметричность распределения подвижного бора. Если бы расчетная величина критерия Стьюдента была меньше табличной, то распределение отнесли бы к симметричному даже при наличии незначительной асимметрии.
Эксцесс кривой распределения (Е) имеет место в тех случаях, когда большинство вариантов совокупности сосредоточено около среднего арифметического. Тогда эмпирическая кривая распределения отклоняется от нормальной теоретической кривой у ее вершины и количественно выражается показателем эксцесса (рис. 1.3).
Положительный эксцесс представлен островершинной кривой (эксцессивной, или лептокуртичной) (см. рис. 1.3, а), отрицательный – плосковершинной (депрессивной, или платикуртичной) (см. рис. 1.3, б). При сильном отрицательном эксцессе кривая может приобрести вид двухвершинной
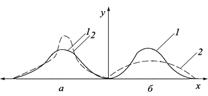
Рис. 1.3. Эксцесс кривой распределения положительный (а) и отрицательный (б):
1 – теоретическая линия распределения, 2 – эмпирическая линия распределения
Показатель эксцесса определяется по формуле:
E = [∑ (x – M)4/ N ·σ4] – 3.
Вычисляют ошибку коэффициента эксцесса: mE = 2 
Оценка достоверности показателя эксцесса производится аналогично оценке показателя асимметрии по критерию Стьюдента: t = E / mE.
Оценить достоверность показателей эксцесса и асимметрии можно более простым способом. Отклонение эмпирического ряда по асимметрии и эксцессу от нормального распределения считают существенным, если Kas и Е более, чем в 3 раза превышают свои ошибки (mas, mE). Если показатель эксцесса меньше –2, это указывает на наличие в выборке вариант, относящихся к разным совокупностям. Эксцесс считается незначительным, если |E| < 0,4. Чем меньше показатель эксцесса, тем ближе распределение к нормальному.
Асимметрия и эксцесс эмпирических кривых указывают иногда на важные особенности объекта исследования, например, на изменение признака в ходе усовершенствования технологии на предприятии при выпуске той же продукции. В таких случаях изучение степени и характера асимметрии и эксцесса вариационных кривых может быть самостоятельной задачей при проведении исследовательских работ.
20 Линейные модели активно используются в экономике и экономической географии как достаточно эффективные в ряде ситуаций. Линейная функция (тройное правило) самая удобная, простая, хорошо разработанная математическая модель.
Линейное программирование – это совокупность методов решения экстремальных задач, в которых цель (критерий оптимальности) и условия (ограничения) заданы уравнениями и неравенствами первой степени. Программирование используется в данной ситуации как планирование, линейное – означает, что ищется экстремум линейной целевой функции при линейных ограничениях (линейных уравнениях, линейных неравенствах). Однако вычислительные средства при решении задач этого класса играют существенную роль в повышении эффективности их приложений.
Для решения задач с применением линейного программирования эффективны следующие:
· составление смеси продукции предполагает выбор наиболее экономичного топлива, пищевых продуктов и т. д.;
· задачи производства – подбор наиболее выгодной производственной программы выпуска одного или нескольких видов продукции при использовании некоторого числа ограниченных источников сырья;
· задачи распределения, или транспортные задачи;
· комбинированные задачи – производство товаров в разных местах, задачи производства и распределения объединяют в единую задачу.
Разработан ряд алгоритмов, среди которых наиболее известны симплексный и распределительный методы. Наиболее эффективен метод эллипсоидов (графический). Оба метода базируются на последовательном улучшении первоначального плана путем повторения вычислений (интераций). После каждой интерации значение целевой функции улучшается. Процесс повторяется до получения оптимального плана, а полученный план проверяется на оптимальность простыми критериями.
Симплекс-метод более универсален, так как позволяет решать задачи, условия которых выражены в различных единицах измерения. В задачах, решаемых распределительным методом (транспортные задачи), все переменные должны иметь одну и ту же единицу измерения. Транспортные задачи являются специальной разновидностью симплекс-метода
21 (неточно)Распределительная модель линейного
программирования
Распределительный метод среди задач линейного программирования получил распространение из-за упрощения расчетов, точности вычислений и снижения затрат времени на ввод исходной информации. Метод предложили А. Толстой и Л. В. Конторович в 1939 – 40 гг. Первоначально он применялся в задачах, связанных с транспортировкой грузов, их распределением между поставщиком и потребителем, поэтому получил название «транспортная задача». Применяется при решении ряда землеустроительных задач: распределение севооборотов и угодий по участкам, размещение культур на землях различных категорий, перераспределение участков между хозяйствами для экономии транспортных затрат и др.
Суть распределительной задачи следующая. Заданы m источников ресурса (производители продукции, базы с готовой продукцией) и n пунктов его потребления. Запасы ресурса в источниках составляют Аi, i=1,…, m, потребности – Bj, j=1,…, n. Стоимость транспортировки единицы ресурса от i-го источника к j-му потребителю Сij. Количество ресурса, транспортируемого от i-го источника к j-му потребителю Хij. Требуется определить такие значения Хij, при которых общие транспортные расходы будут минимальны.
При сбалансированности, когда общий спрос на запас ресурса у поставщиков и общий спрос на него у потребителя равны, задачу называют закрытой:
.
Если баланс не выдерживается, то транспортная задача является открытой: 
, или 
.
При наличии баланса модель транспортной задачи формулируется следующим образом.
Целевая функция: 
Условия. Ограничения по запасам: 
Ограничения по потребностям: 
Условие баланса: 
Условие неотрицательности:
Xij ≥ 0, i = 1,…,m, j = 1,…,n.
Особенности распределительных транспортных задач следующие:
· условия задачи описываются уравнениями (в симплекс-методе описываются и неравенствами);
· все переменные выражаются в одних и тех же единицах измерения;
· во всех уравнениях коэффициенты при переменных равны единице;
· каждая переменная встречается только в двух уравнениях системы ограничений: в одном по строке (по запасам) и в одном по столбцу (по потребностям).
Целевая функция Z выражает суммарные расходы на транспортировку грузов. Ограничения по запасам и по потребностям означают, что сумма ресурса, забираемого из i-го источника, должна быть равна запасу ресурса в нем, как и сумма ресурса, доставляемого j-му потребителю, должна быть равна его потребности.
Величина Сij может выражать транспортные расходы (минимизация) или прибыль от транспортных операций (максимизация) и другие показатели.
.
22 Транспортные задачи могут быть открытыми, учитывать время транспортировки продукции, затраты на производство единицы продукции, многоэтапными, многопродуктовыми. Все они, как и закрытая транспортная задача, являются частным случаем более сложной лямбда-задачи. Рассмотрим некоторые из них.
Транспортная задача, в которой суммарная мощность поставщиков не совпадает с суммарным спросом потребителей, называется открытой. В связи с этим условия модели записываются как: ∑ai > ∑ bj или ∑ai < ∑bj. Для решения открытой транспортной задачи могут применяться методы: потенциалов, дельта-метод, МОДИ.
В географических исследованиях, посвященных вопросам определения границ зон сбыта продукции или рациональных связей по прикреплению потребителей к поставщикам, должны учитываться не только транспортные, но и производственные затраты. Такие задачи получили название транспортно-производственных. В качестве cij = Si + tij выступают транспортно-производственные затраты, т. е. Si – затраты на производство единицы продукции (себестоимость, цена единицы продукции или приведенные удельные затраты) i-м поставщиком; tij – затраты на перевозку продукции между i-м поставщиком и j-м потребителем. Суммарные мощности поставщиков равны суммарному спросу потребителей. Следовательно, какой бы ни была стоимость производства, потребители для удовлетворения своего спроса возьмут продукцию у всех поставщиков. От каких поставщиков получит каждый потребитель продукцию, зависит от транспортных затрат. Модель транспортно-производственной задачи при введении дополнительных условий можно использовать для оптимизации развития и размещения промышленного производства, получить ответ, где должны располагаться новые промышленные объекты.
Для решения этих закрытых и открытых задач используются рассмотренные методы функционала, потенциала.
В современных условиях перевозка продукции от поставщика к потребителю осуществляется двумя путями: поставщик → потребитель (наиболее экономически выгодный) и поставщик → база → потребитель (требует больше транспортных и иных затрат). Поставка продукции через базу к потребителю требует построения модели многоэтапной транспортной задачи, в которой за критерий оптимальности обычно принимается минимальное значение совокупных транспортных затрат. Способ решения транспортных задач с двумя и более этапами предложен американским ученым А. Орденом. Впоследствии его назвали способом фиктивной диагонали.
Однако иногда возникает необходимость составления базисного плана перевозок взаимозаменяемых видов продукции. Такой вопрос следует решать как единую задачу, так как в ней различные продукты могут приравниваться друг к другу через переводные коэффициенты. Решение задачи данной модели не имеет принципиальных отличий от решения закрытой однопродуктовой задачи. Существуют лишь специфические методические приемы обработки исходной информации, которые необходимо знать, чтобы подготовить матрицу для выполнения расчетов.
Алгоритм транспортных задач по методам решения значительно проще, чем лямбда-задачи. Ее называют распределительная или обобщенная транспортная задача. В ее модели отражается более широкий круг практических задач богатых по содержанию.
23.Показатели центра распределения.Для обоснования представления о генеральной совокупности на основании выборки необходимо использовать наиболее характерные параметры признаков. К ним относятся показатели центра распределения, или среднего положения: мода, медиана, среднее арифметическое, гармоническое, геометрическое, квадратическое, кубическое, взвешенное. Средняя величина выражает характерную, типичную для данного ряда величину признака и является равнодействующей всех факторов, влияющих на признак. В ней погашаются индивидуальные различия вариант в ряду, обусловленные случайными обстоятельствами.
Мода (Мо) представляет собой наиболее часто встречающуюся варианту в вариационном ряду. На графике она соответствует максимальной ординате и находится на вершине вариационной кривой. Если вариационный ряд разбит на классы, то мода соответствует максимальной частоте класса, который называется модальным. При полимодальном (многовершинном) распределении вариационный ряд имеет несколько значений моды.
Медиана (Ме) представляет собой среднюю варианту в ранжированном вариационном ряду, которая делит его на две равные части. При нечетном числе вариант середину ряда будет составлять одна варианта (медиана). При четном числе вариант середину ряда образуют две варианты, среднее арифметическое которых будет характеризовать медиану.
При наличии в вариационном ряду сильно отличающихся вариант медиана будет характеризовать середину ряда более точно, чем среднее арифметическое. Мода и медиана используются в тех случаях, когда о выборочных параметрах необходимо иметь ориентировочное представление.
Среднее арифметическое (М, 
)представляет собой величину, сумма положительных и отрицательных отклонений от которой равна нулю. Оно является основной характеристикой статистической совокупности и вычисляется по формуле: М = ∑ хi / N, где ∑ хi – сумма всех вариант совокупности. Среднее арифметической рассчитывается в тех случаях, когда противопоказано вычислять другие средние.
Пример. Определено следующее количество осадков, выпавших в трех пунктах наблюдений: 10, 15 и 20 мм (N = 3). Среднее арифметическое равно: М = (10+15+20) / 3 = 15 мм.
Среднее гармоническое (Мгар)вычисляется при усреднении меняющихся скоростей процессов (скорость течения воды), показателей обратно пропорциональной зависимости между процессами и явлениями, сложных абсолютных величинах измерений (тонна/километр). Оно рассчитывается по формуле: Мгар= N / ∑ (1 / хi). Его величина меньше, чем средней арифметической. Для вычисления сохраним те же количественные варианты, что и для определения среднего арифметического.
Пример. При измерении скорости воды в реке на трех створах русла получены следующие результаты: 10, 15 и 20 м/с:
Мгар = 3/ ∑ [(1:10) + (1:15) + (1:20)] = 13,8 м/с.
Среднее геометрическое (Мг)вычисляетсяв тех случаях, когда в вариационном ряду отдельные значения распределяются в геометрической прогрессии (резко различаются между собой, например, 4 и 16). В данном случае среднее геометрическое равно 8. Оно в два раза меньше 16 и в два раза больше 4. Среднее арифметическое из этих вариант 10, т. е. больше среднего геометрического. При наличии нулевой варианты рассчитывается приближенное среднее арифметическое. Если варианты представлены логарифмами чисел (рН и др.), то вычисляют среднее логарифмическое.
Пример. Строение стоит 100 тыс. у.е. Одним лицом оно оценивается в 10 млн, другим – в 1000 млн. С арифметической точки зрения в первом случае получаем ошибку в 90 млн у. е., во втором – в 900 млн у.е. Если оценивать, во сколько раз ошиблись покупатели, то получаем один ответ в обоих случаях – в 10 раз.
Среднее квадратическое (Мкв) используется, когда необходима проверка результатов эксперимента на единство суммарного действия (средний радиус или диаметр объекта, площадь земельных участков, функциональных зон и т.д.).
Пример. Имеются данные по величине радиусов трех спилов дуба: 10, 15 и 20 см. Среднее квадратическое будет равно:
Мкв = 
= 
= 15,56 см.
Среднее кубическое (Мкуб)применяется при проверке на единство суммарного действия, например, при нахождении средней величины объема.
Пример. Кубатура древесины по трем ключевым участкам составляет 10, 15, и 20 м3. Определяем среднее кубическое по формуле:
Мкуб = 
= 
= 16,03 м3.
Величина средней кубической максимальна по сравнению с другими средними и находится в ряду справа всех средних: Мгар<Мг<М <Мкв<Мкуб.
Средне взвешенная (Мвзв). Сгруппированный вариационный ряд по классам иногда называют взвешенным из-за той роли, которую выполняют частоты. Чем больше частота вариант в классе, тем больший вес она имеет в характере распределения числового ряда. Среднее арифметическое, рассчитанное в этом ряду, называют взвешенным средним:
Мвзв = ∑[(x1 · f1) + (x2 · f2) + …+ (xn · fn)] / ∑ fi,
где хn – варианты; fi – частоты по классам.
Если совокупность вариант разбита на несколько неравных по численности групп, то среднюю арифметическую вычисляют для каждой группы. Затем их объединяют, определяя общее среднее (Мобщ):
Мобщ = ∑ Мj · nj / ∑ nj ,
где Мj – среднее по группам; nj – число вариант в группе.
24 Существует несколько способов составления допустимого (базисного) плана: северо-западного угла, поисков наименьшего элемента в столбце, наименьшего элемента в строке, наименьшего элемента в матрице. Роль наименьшего элемента выполняет Cij (цифры в правом верхнем углу клеток матрицы). Способ северо-западного угла более сложный и в случае большой матрицы не рекомендуется его использование. Если столбцов меньше, используют поиски наименьшего Cij в столбцах; если строк мало – способ поиска наименьшего элемента в строках; если матрица большая, проводится поиск наименьшего элемента в клетках матрицы. Проведем распределение поставок перечисленными выше способами при одинаковых исходных данных и для сравнения вычислим их функционалы 
min
Способ северо-западного угла.
Поставки распределяем по диагонали не зависимо от величины Cij
Остаток поставок распределяем между потребителями с учетом минимальных значений Cij:
Способ поиска наименьшего Сij в столбце. Поставки распределяются последовательно по столбцам с учетом наименьших Сij.
Способ поиска наименьшего элемента Сij в строке. Поставки распределяем последовательно сверху вниз по строкам с учетом наименьших величин Cij:
Способ поиска наименьшего элемента Cij в матрице. Поставки распределяются начиная с поиска наименьших величин Cij в матрице
На основании распределения поставок получаем функционалы Z
Сопоставляя величины функционала (Z), полученные в результате составления базисного плана, получаем вывод:(напрмер: наименьший функционал (215), а значит, и наиболее оптимальное первоначальное распределение поставок получено в нашем примере по способу наименьшего элемента в матрице и строке.)
26 Правила построения цепи:
Цепь должна быть замкнутым многоугольником.
В цепи четное число вершин.
Все углы цепи прямые.
Отрезки цепи могут проходить через клетки матрицы, не являющиеся вершинами данной цепи, хотя в них могут содержаться поставки.
Положительными (плюсовыми) вершинами будут клетки, в которых при перераспределении по цепи поставки увеличиваются.
Отрицательными (минусовыми) вершинами являются клетки, в которых поставки при перераспределении уменьшаются.
В цепи положительные вершины чередуются с отрицательными, количество их равно между собой.
Вершина-квадрат, куда вносится поставка в ходе перераспределения, всегда положительная.
При перераспределении поставок по цепи можно двигаться только по горизонтали или вертикали, изменяя направление только в вершинах цепи.
Клетки, пересекаемые отрезками цепи, вершинами не являются, но в цепи отражаются в виде изломанной линии.
Алгебраическая сумма чисел в вершинах цепи Cij (–2 + 3 – 4 + 1 = = –2) показывает, насколько может измениться значение функционала, если внести в вершину-квадрат поставку, равную 1. Сумму называют характеристикой цепи. Минусовая сумма указывает на уменьшение величины функционала, плюсовая – на увеличение. Эта величина равна произведению характеристики цепи (–2) на величину поставки (Хij), которую мы перемещаем по цепи (5), т. е. –2 ∙ 5 = –10.
27 Выбор конкретной методики оценки различий по критерию Стьюдента зависит от учета следующих особенностей выборочных совокупностей: сравниваются средние арифметические в независимых (несвязанных) выборках; различия устанавливаются в сопряженных (парных) выборках; устанавливается различие между выборочными и генеральными средними (теоретическими стандартами).
Независимые статистические совокупности могут быть получены на одном или нескольких объектах, но при одинаковых условиях проведения эксперимента: например, измерение температуры воздуха в январе в г. Бресте на протяжении нескольких лет и установление достоверных различий между этими показателями по годам исследований; сравнение экономического показателя в хозяйстве или на предприятии по пятилеткам между собой; сравнение чистого дохода в хозяйствах с одинаковым экономическим развитием, но расположенных на значительном расстоянии. При сравнении независимых выборочных совокупностей объемы выборок могут быть одинаковы (N1 = N2) или разные (N1 ≠ N2). В двух сравниваемых независимых выборках с одинаковым или разным объемом наблюдений степень свободы определяется по формуле: ν = (N1–1) + (N2 – 1) = N1 + N2 – 2.
При малых объемах независимых совокупностей, если дисперсии сравниваемых выборок нельзя считать одинаковыми, число степеней свободы определяется сложнее: ν = 
,
где u = 
/( 
+ 
); 
и 
– ошибки среднего арифметического первой и второй выборок соответственно.
Сопряженные статистические совокупности получают на одном или на разных объектах, но в разных условиях. Например, сравнение температуры воздуха в июле и январе г. Могилева; сравнение прибыли фермерских и подсобных хозяйств в любом районе или фермерских хозяйств Витебской и Гомельской области. Объем сравниваемых выборок должен быть одинаков (N1 = N2). Определение степени свободы для сопряженных выборок определяется как: ν = Nпар – 1.
29Критерий Стьюдента.Используется для оценки сходства или различия между выборочными совокупностями по разности величин их средних арифметических (d = Mбольшая – Мменьшая) и ее отношения к ошибке этой разности (md) при условии распределения вариант в группах по закону нормального распределения и подтверждается равенство разброса вариант в выборке (близкие дисперсии сравниваемых выборок). Не допускается применения критерия в случае балльного характера сравниваемых числовых признаков.
Критерий Стьюдента определяют по формуле:
t = d / md = (Mбольшая – Мменьшая) / md . (1.19)
Сопоставляя критерий Стьюдента вычисленный с табличным устанавливают или отвергают с некоторой долей уверенности различия между средними арифметическими выборок.
В большинстве исследований для статистической проверки гипотез существенности различий средних арифметических используют параметрический критерий Стьюдента.
Метод потенциалов
Метод разработан в 1940 г. академиком Л. В. Конторовичем. В 1951 г. американским ученым Дж. Б. Данцигом предложен распределительный метод (МОДИ), аналогичный методу потенциалов. В обоих методах при проверке допустимого плана на оптимальность определяются потенциалы (числа), с помощью которых вычисляются характеристики клеток без кружков (в них нет поставок).
Обозначив потенциалы строк через Ui, потенциалы столбцов через Vj, показатели Cij в клетках с поставками и кружками через 
, характеристики клеток без кружков (без поставок) через Eij. получим следующие соотношения::
метод потенциалов метод МОДИ
ui = vj – 
; (8.10) ui = 
– vj;
vj = 
+ ui; (8.11) vj = 
– ui;
= vj – ui; (8.12) = vj + ui;
Eij = cij – (vj – ui); (8.13) Eij = cij – (vj + ui).
Каждый показатель 
(в клетке матрицы он находится в кружке) должен быть равен разнице потенциалов своих столбцов и строк. Определение потенциала можно начинать с любой строки или столбца. Первый потенциал по величине выбирается произвольно (лучше определение начинать с нуля). Величины других потенциалов определяются с использованием предложенных выше формул (при первом вычислении применяется выбранный нами потенциал).
Рассмотрим пример решения транспортной задачи, предложенный В. С. Михеевой (1981). Базисный допустимый план составлен способом наименьшего элемента в столбце, его первоначальный функционал 555 (табл. 8.4).
Вначале рассчитаем потенциалы строк и столбцов по методу потенциалов с использованием формул. Произвольно выбранную величину потенциала выбирает в том столбце или строке, где наибольшее количество клеток с кружками. В нашем примере – это третья строка. В качестве потенциала для нее возьмем число 0. По формуле (8.11) определяем потенциалы (vj) первого (vj = 
+ ui = 0 + 2 = 2), третьего (0 + 6 = 6), четвертого (0 + 4 = 4), пятого (0 + 2 = 2) столбцов. Зная потенциалы по четырем столбцам, можно вычислить потенциалы строк (ui) по формуле (8.10): первой (ui = vj – = 2 – 1 = 1), четвертой (6 – 2 = 4). По полученным потенциалам новых строк вычисляем потенциалы новых столбов, а по ним – новых строк (см. табл. 8.4).
Определив потенциалы строк и столбцов, вычисляют характеристики клеток (Eij) без кружков (в них нет поставок) по формуле (8.13). Приведем расчет характеристики клетки 1.2: Eij = cij – (vj – ui) = 2 – (7 – 1) = – 4. Аналогично рассчитываем Eij (показаны курсивом) для других клеток без кружков.
отрицательные величины получены в клетках матрицы 1.2, 1.3, 3.2 (их величины соответственно: – 4, –2, –2), поэтому составленный первичный базовый план не оптимален. Проводят следующее перераспределение поставок по правилам цепи.
Выбираем клетку с наибольшей отрицательной абсолютной величиной характеристики (E12) равную – 4. К клетке 1.2 строится цепь по перемещению наименьшей поставки 5 из клетки 3.3, так как функционал стремится к минимуму. Путь перемещения следующий: 3.3 (–5)"4.3 (+5)"4.2 (–5)"1.2 (+5)"1.1 (–5)"3.1 (+5)"3.3. К имеющейся поставке в клетке прибавляется или отнимается 5 с целью сохранения баланса между поставщиками и потребителями.
Получаем новую матрицу с измененными поставками (8.5). В ней повторяем алгоритм расчетов, как в табл. 8.4: рассчитываем потенциалы строк и столбцов, характеристику клеток без поставок, производим перераспределение поставок с использованием другой минимальной поставки 25 в клетке 3.4. Другая минимальная поставка 25 в клетке 3.1 перемещаться не может по цепи, так как в свободной клетке 4.4 с максимальной отрицательной абсолютной характеристикой (–3) ее следует вычитать из несуществующей поставки. Поставка 25 в клетке 3.4 перемещается по цепи: 3.4 (–25)"3.1 (+25)"1.1 (–25)"1.2 (+25)"4.2 (–25)"4.4 (+25)"3.4 (цепь замыкается). Расчет потенциалов и характеристики в новой матрице показал, что распределение не оптимально. Получена отрицательная характеристика –1 в клетке 4.5. Следует произвести очередное перераспределение следующей минимальной поставки равной 0 в клетке 1.1. Здесь получена нулевая поставка, так как из прежней поставки в клетке 25 следовало вычесть перераспределяемую 25. В таких ситуациях допускается наличие нулевой поставки, чтобы не нарушались правила перемещения поставки по цепи. Результаты распределения представлены в матрице 3 (табл. 8.6). В ней снизилось отрицательное значение Eij до –1. План приблизился к оптимальному и требуется его усовершенствовать. Проводим очередное перераспределение поставок. Минимальную нулевую поставку из клетки 1.1 перемещаем в клетку 4.5, где отрицательная характеристика клетки. Прибавление и вычитание нуля по цепи не изменяет величины поставок в клетках и не нарушает правил построения цепи. В новой матрице 4 (табл. 8.7) после перерасчетов vj, ui, Eij получены все положительные характеристики цепи при стремлении функционала к минимуму, поэтому план распределения поставок оптимальный, величина Z = 460. По сравнению с базовым планом функционал снизился на 95 единиц.
В задачах при стремлении функционала к максимуму план распределения поставок или иного показателя считается оптимальным, если в матрице получены отрицательные характеристики в клетках.
31Наименьшая существенная разность(НСР). Используется в дисперсионном анализе. Она показывает то минимальное различие между средними, начиная с которого при выбранном уровне вероятности средние сравниваемые показатели существенно отличаются друг от друга. Величина критерия выражается в тех же единицах, что и сравниваемые средние выборочных совокупностей и определяется по формуле:
НСР = tтабл ∙ md ,(1.24)
где md – ошибка разницы средних; tтабл – табличное значение критерия Стьюдента при уровне вероятности 0,95 или 0,99 и степени свободы, определяемой экспериментом.
Если разность между сравниваемыми средними в условиях эксперимента больше или равна величине НСР при Р 0,95 или 0,99, то различие сущеcтвенно. Используя предыдущий пример по глубине расчленения рельефа, проверим достоверность разницы между средними арифметическими с использованием критерия НСР для случаев независимого и сопряженного наблюдений по формуле (1.24):
НСР0,95 = 2,31 ∙ 1,40 = 3,23 м; НСР0,99 = 3,36 ∙ 1,40 = 4,70 м (для независимых наблюдений);
НСР0,95 = 3,18 ∙ 0,40 = 1,27 м; НСР0,99 = 5,84 ∙ 0,40 = 2,33 м (для сопряженных наблюдений.
Разница между средними арифметическими глубины расчленения рельефа при независимых и сопряженных наблюдениях одна и та же (1,4 м). Сравнивая ее с величиной НСР, приходим к тем же выводам. что и при использовании критерия Стъюдента.
33Критерий Фишера.В выборочных совокупностях дисперсии могут существенно отличаться друг от друга. В таких случаях установление различий между выборочными совокупностями проводится по критерию Фишера (F – положительное асимметричное распределение). Расчет производится по формуле:
F = σ2большая/ σ2меньшая(1.25)
Если величина расчетного критерия Фишера (Fф)не превышает величины приведенного в таблице (Fт)(прил. 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф > Fтэти дисперсии достоверно различны, как и сравниваемые по ним генеральные совокупности. Степень свободы рассчитывается для сравниваемых выборок отдельно по формуле ν = N – 1.
Дельта-метод Аганбегяна
Для решения закрытых и открытых транспортных задач А. Г. Аганбегян (1961) разработал дельта-метод для ручной обработки.
Если в столбце несколько равных по значению cij, выбираем любой из них
.
Отличие построения цепей в дельта-методе:
· цепь строится незамкнутая;
· цепь начинается в клетке с кружком (с поставкой), которая находится в минусовой строке; в этой клетке поставка уменьшается и она становится отрицательной вершиной цепи;
· перемещение поставки в конец открытой цепи производится как в методе потенциалов с чередованием положительных и отрицательных вершин;
· в этом методе не требуется количества кружков (клеток с поставками), равного m + n – 1 ;
· в исходном плане число кружков равно числу столбцов и лишь в ходе решения появляются новые клетки с кружками (поставками);
· в незамкнутой цепи вершинами бывают клетки без кружков (без поставок); они положительны, так как в них вносится поставка;
· характеристика незамкнутой цепи рассчитывается как алгебраическая сумма показателей ∆Сij или 
в ее вершинах; так как при распределении поставок по цепи функционал увеличивается, характеристика цепи всегда положительная; она показывает, насколько увеличивается в функционал, если передвинуть по цепи поставку, равную 1, из минусовой строки в плюсовую.
35Критерий Пирсона (хи-квадрат, χ2).Для оценки соответствия или расхождения полученных эмпирических данных и теоретических (расчетных, прогнозных) распределений применяются статистические критерии согласия. Среди них наибольшее распространение получил непара
Дата: 2016-10-02, просмотров: 227.
