Згідно з рівнянням Бернуллі загальна питома енергія (стосовно одиниці ваги) рідини, яка рухається, виражається рівнянням:

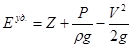, де

Z – висота центру ваги описуваного обсягу рідини над площею порівняння;

Р – тиск у центрі ваги;

V – швидкість рідини;

ρ – питома вага рідини (щільність);

g – прискорення сили ваги.

На підставі цієї формули повна питома енергія рідини на виході з насоса (переріз 2 – 2) буде рівна:

.

Аналогічно в перерізі 1 – 1:

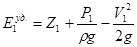, де

Z₁ і Z₂ – висоти центрів ваги перерізів (1–1) і (2–2) над площею (О-О);

Р₁ і Р₂ – абсолютний тиск при вході й при виході з насоса;

V₁ і V₂ – швидкості руху рідини при вході й при виході з насоса.

Напір насоса (тобто різниця питомих енергій) буде рівна:

Враховуючи, що манометри показують тиск манометричний (надлишковий), тому:

Р₂ = Р_атм. + Р_мак.2; де

Р_атм. – атмосферний тиск;

Р_мак.2 – показання манометра в центрі ваги перерізу (2–2) .

Відомо також, що показання манометра залежать від висоти, на якій він установлений.

Так, наприклад, якщо манометр, установлений на оцінці Z₂, перенести в оцінку Z₃, то він буде показувати тиск:

Р_мак.3 = Р_мак.2 + (Z₂ – Z₃)ρg

Вакууметр показує, наскільки тиск у крапці виміру, менше від атмосферного тиску, тобто Р₁ = Р_атм. – Р_вак.1, де

Р_вак.1 – показання вакууметра в центрі ваги перерізу (1 – 1).

Показання вакууметра також залежать від висоти його установки. Будучи встановленим на оцінці Z₃, він покаже величину:

Р_вак.3 = Р_вак.1 – (Z₁ – Z₃)ρg

З обліком вищесказаного формула запишеться:

Таким чином, напір насоса рівняється сумі показань манометра на напірному патрубку й вакууметра на усмоктувальному патрубку, наведених до одній висотній оцінці й плюс різницю швидкісного напору в напірному й усмоктувальному патрубках насоса. Найбільше часто показання манометра й вакууметра приводять до оцінки осі насоса.

Враховуючи зв'язок напору й тиску, формула для визначення тиску буде:

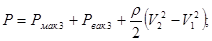
Якщо насос працює з підпором (під затокою), то на усмоктувальному трубопроводі замість вакууметра ставлять манометр. У такому випадку напір насоса буде рівний:

А тиск

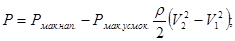
Рух рідини в робочім колесі

Відцентрового насоса

Рідина в середині межлопастного каналу робочого колеса обертається разом з робочим колесом (тобто здійснює переносний рух). Крім того, вона ще переміщається й щодо робочого колеса, переміщаючись від центру колеса до його периферії (при цьому вона виконує відносний рух). У зв'язку із цим розрізняють такі види швидкостей руху часточок рідини в робочім колесі відцентрового насоса:

1 – швидкість переносного руху (окружна швидкість) – U;

2 – швидкість відносного руху – W;

3 – швидкість абсолютного руху – V, яка є сумою векторів переносний і відносної швидкостей V = U + W.

В основу теоретичної вистави про усталений рух потоку рідини через робоче колесо відцентрового насоса покладена гіпотеза про струминний рух. Виходячи із цієї гіпотези кожна частка рідини в середині міжлопатевого каналу рухається по траєкторії, форма якої збігається із кривої малюнка лопатки.

Швидкість переносного руху U завжди спрямована по дотичній до кола, по якому обертається крапка. Напрямок цієї швидкості збігається з напрямком обертання. Для часточки рідини, яка перебуває в міжлопатевому просторі каналу на відстані τ від центру обертання, величина переносної (окружний) швидкості визначиться:

де
W – кутова швидкість колеса;

n – кількість оборотів колеса у хвилину.

Згідно з гіпотезою про струминний рух рідини W (відносна швидкість) завжди буде спрямована по дотичній до поверхні лопатки убік виходу з робочого колеса. Величина цієї швидкості буде зменшуватися в міру переміщення часточки рідини від центру периферії робочого колеса, тому що збільшується перетин міжлопатевих каналів.

Абсолютна швидкість руху часточки рідини визначається як сума двох векторів U і W за правилом паралелограма.