Сгенерировать секретные ключи для абонентов A, B, C, D и по методу Диффи-Хеллмана (DH). Для этого взять значение g из таблицы 1.1 (i - предпоследняя цифра номера зачетной книжки), а значение р подобрать согласно методическим указаниям.
Число j (последняя цифра номера зачетной книжки) – номер для первого абонента (абонента А) при выборе числа ХА. Значения XB, XC, XD, XE для остальных четырех абонентов необходимо выбрать по циклической процедуре, прибавляя каждый раз по единице.
Например, цифры в зачетной книжке (15). Выбираем число g = 3, т.к. i= 1. Значение ХА равно 29 (т. к. j =5). Для второго абонента значение ХВ будет равно 31 (j =5+1=6), Для третьего ХС = 37, т. к. j =7. Для пятого выбираем ХЕ = 41, т.к. j=9. Если, например, последняя цифра номера зачетной книжки 7 (больше пяти), то выбираем ХА=37, ХВ=39, ХС=41, ХD=7, ХE= 11.
Таблица 1.1 Исходные данные для числа g :
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| g | 1 | 3 | 5 | 11 | 23 | 29 | 41 | 101 | 113 | 179 |
Таблица 1.2 Исходные данные для чисел XA, XB, XC, XD, XE:
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| X | 7 | 11 | 13 | 17 | 19 | 29 | 31 | 37 | 39 | 41 |
Методические указания к решению задания 2.1
Первая система с открытым ключом — система Диффи-Хеллмана.
Эта криптосистема была открыта в середине 70-х годов американскими учеными Диффи (Whitfield Diffie) и Хеллманом (Martin Hell-man) и привела к настоящей революции в криптографии и ее практических применениях. Это первая система, которая позволяла защищать информацию без использования секретных ключей, передаваемых по защищенным каналам. Для того чтобы продемонстрировать одну из схем применения таких систем, рассмотрим сеть связи с N пользователями, где N — большое число. Пусть мы хотим организовать секретную связь для каждой пары из них. Если мы будем использовать обычную систему распределения секретных ключей, то каждая пара абонентов должна быть снабжена своим секретным ключом, т.е. всего потребуется 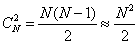 ключей.
ключей.
Если абонентов 100, то требуется 5000 ключей, если же абонентов 104 , то ключей должно быть 5∙107. Мы видим, что при большом числе абонентов система снабжения их секретными ключами становится очень громоздкой и дорогостоящей.
Диффи и Хеллман решили эту проблему за счет открытого распространения и вычисления ключей. Перейдем к описанию предложенной ими системы.
Пусть строится система связи для абонентов А,В,С,... .У каждого абонента есть своя секретная и открытая информация. Для организации этой системы выбирается большое простое число р и некоторое число g, 1 < g < р — 1, такое, что все числа из множества {1, 2, ∙ ∙ ∙ ,р — 1} могут быть представлены как различные степени g mod p (известны различные подходы для нахождения таких чисел g, один из них будет представлен ниже). Числа р и g известны всем абонентам.
Абоненты выбирают большие числа Xa,Xb,Xc, которые хранят в секрете (обычно такой выбор рекомендуется проводить случайно, используя датчики случайных чисел). Каждый абонент вычисляет соответствующее число Y, которое открыто передается другим абонентам,
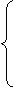 YА = gXa mod р ,
YА = gXa mod р ,
YB = gXb mod р.. (1)
Yс = gXc mod р.
В результате получаем следующую таблицу.
Таблица 1.3 Ключи пользователей в системе Диффи-Хеллмана
| Абонент | Секретное число | Открытый ключ | Закрытый ключ |
| A B C | XA XB XC | YA YB YC | ZAB, ZAC ZBA, ZBC ZCA, ZCB |
Допустим, абонент А решил организовать сеанс связи с В, при этом обоим абонентам доступна открытая информация из табл. 2. Абонент А сообщает В по открытому каналу, что он хочет передать ему сообщение. Затем абонент А вычисляет величину
ZAB = (YB)ХА modp (2)
Никто другой, кроме А, этого сделать не может, так как число ХА секретно.
В свою очередь, абонент В вычисляет число
ZBA = (YA)XBmodp (3)
На рисунке 1 представлена схема обмена ключами в системе Диффи-Хеллмана.
Остановимся теперь на упомянутой выше задаче выбора числа р.
При произвольно заданном g она может оказаться трудной задачей, связанной с разложением на простые множители числа g - 1.
Дело в том, что для обеспечения высокой стойкости рассмотренной системы число g - 1 должно обязательно содержать большой простой множитель.
Поэтому часто рекомендуют использовать следующий подход.
Число р выбирается таким, чтобы выполнялось равенство
р=2q+1 (где q- также простое число)
и были справедливы неравенства
1 < g < р - 1 и gq mod р 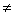 1.
1.
Для того чтобы система была устойчива к криптоанализу, необходимо выбирать число р очень большим.
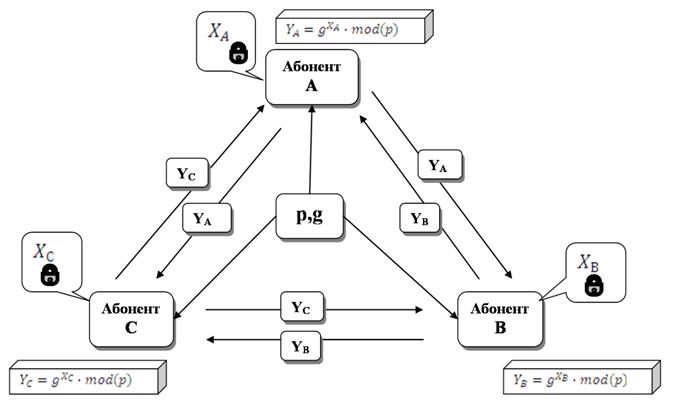
Рисунок 1 - схема обмена ключами в системе Диффи-Хеллмана
Пример 2.1. Пусть g = 43. Выберем параметр p. Попробуем взять q=17 401.
Соответственно р=2*17 401+1=34 803. Проверим: 4317401 mod 34 803 = 17 746. Необходимые условия выполняются, значит, такое р подходит. Итак, мы выбрали параметры р = 34 803, g = 43. Теперь каждый абонент выбирает секретное число и вычисляет соответствующее ему открытое число. Пусть выбраны ХA = 7, ХB = 13. Вычисляем YA = 437 mod 34 803 = 11 689, YB = 4313 mod 34 803 = 14 479. Пусть А и В решили сформировать общий секретный ключ. Для этого А вычисляет ZAB = 144797 mod 34 803=6 415, а В вычисляет ZBA = 11 68913 mod 34 803 = 6 415. Теперь они имеют общий ключ 6 415, который не передавался по каналу связи.
Контрольные вопросы
1. Какими преимуществами перед другими алгоритмами с закрытым ключом обладает система Диффи-Хеллмана?
2. Дайте краткую характеристику системы Диффи-Хеллмана.
3. Объясните, почему число р, необходимое при вычислении секретных ключей, следует выбирать большим?
2.2 Шифрование по алгоритму Шамира
Зашифровать сообщение по алгоритму Шамира для трех абонентов, взяв значение сообщения m и значение p из таблиц 2.1 и 2.2 соответственно. По номеру j (последняя цифра номера зачетной книжки) выбирается требуемое для реализации этого алгоритма число р. По i (предпоследняя цифра номера зачетной книжки) студент выбирает сообщение для зашифровывания, передаваемое первым абонентом. Выбор сообщений для других абонентов производится циклически, согласно процедуре (i + 1). Например, последние цифры номера зачетной книжки – (63). Выбираем для трех абонентов p = 41, mA=24, mB=24, mC=24.
Таблица 2.1 – исходные данные для выбора сообщений ( m )
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Сообщение ( m ) | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 |
Таблица 2.2 – исходные данные для выбора числа р
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| р | 29 | 31 | 37 | 41 | 43 | 47 | 49 | 51 | 53 | 57 |
Дата: 2019-11-01, просмотров: 301.