АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Расчетно-графические работы

ZITS 2221- Основы безопастности в телекоммуникационных системах по

специальности 5В071900–«Радиотехника, электроника и телекоммуникации»

Рассмотрено и одобрено на заседании кафедры ТКСиС

Протокол № __ от __ ______ 2019 г.,

Зав каф. ТКСиС _____________ Темирканова Э.К

Составила: проф _______________.Якубова М.З,

Алматы 2019

Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра "Телекоммуникационные системы и сети"

Дисциплина

«ОСНОВЫ БЕЗОПАСНОСТИ В ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ»

Методические указания к выполнению расчетно - графических работ

для студентов по специальности 05071900 -

– Радиотехника, электроника и телекоммуникации

Алматы 2019

СОСТАВИТЕЛИ: А.С. Байкенов, Шкрыгунова Е.А., Якубова М.З. Основы безопасности в телекоммуникационных системах. Методические указания к выполнению расчетно-графических работ для студентов очной формы обучения специальности 05071900 – Радиотехника, электроника и телекоммуникации – Алматы; АИЭС, 2009 – 22 с.

Методические указания содержат общие положения по выполнению расчетно-графических работ. Приводится рекомендуемая литература.

Содержание

1 Введение…………………………………………………………………...4

Расчетно-графическое задание № 1……………………………………….4

Задание 1.1…………………………………………………………………..4

Методические указания к решению задания 1.1………………………….5

Задание 1.2…………………………………………………………………..7

Расчетно-графическое задание № 2……………………………………..12

Задание 2.1…………………………………………………………………12

Методические указания к решению задания 2.1……………………… 12

Задание 2.2…………………………………………………………………15

Методические указания к заданию №2.2……………………………… 15

Задание 2.3…………………………………………………………………18

Методические указания к заданию 2.3………………………………… 19

Список литературы ……………………………………………………….21

Введение

Целью расчетно-графических работ является ознакомление студентов с математической основой построения систем защиты информации в телекоммуникационных системах - методами криптографии. Расчетно-графические работы направлены на формирование у студентов систематизированного представления о принципах, методах и средствах реализации защиты данных.

Расчетно-графические работы посвящены изучению систем шифрования с закрытым и открытым ключом. Расчетно-графическая работа №1 посвящена шифрованию с закрытым ключом. Рассматриваются алгоритмы RSA, а также предлагаются расчеты по электронной подписи с использованием хеш-функции

Расчетно-графическая работа №2 посвящена асимметричному шифрованию или шифрованию с открытым ключом. Рассматриваются алгоритмы Дифи –Хелмана, Шамира, Эль-Гамаля.

1 Расчетно-графическое задание № 1

Несимметричное шифрование – дешифрование.

Зашифровать информацию по методу RSA для последующей передачи. Вариант задания определяется последними цифрами номера студенческого билета. По номеру i (предпоследняя цифра) студент выбирает сообщение для зашифровывания, по j – требуемые для реализации этого алгоритма числа р и q.

Таблица 1.1 - Исходные данные:

i	0	1	2	3	4
Сообщение	Принтер	Интеграл	Минус	Модуль	Плюс
j	0	1	2	3	4
p q	7.11	5.17	3.11	11.19	13.17

Продолжение таблицы 1.1

i	5	6	7	8	9
Сообщение	Число	Дробь	Корень	Остаток	Степень
j	0	1	2	3	4
p q	7.17	5.11	7.13	11.17	5.13

Методические указания к решению задания 1.1

Одним из наиболее распространенных методов несимметричного шифрования- дешифрования является метод шифрования с открытым ключом, в котором используется алгоритм RSA.

Алгоритм основан на использовании операции возведения в степень модульной арифметики. Его можно представить в виде следующей последовательности шагов:

Шаг 1. Выбирается два больших простых числа числа р и q. Простыми называются числа, которые делятся на самих себя и на 1. На практике для обеспечения криптостойкости системы величина этих чисел должна быть длиной не менее двухсот десятичных разрядов.

Шаг 2. Вычисляется открытая компонента ключа n

n = р q .

Шаг 3. Находится функция Эйлера по формуле

f (р q .)=(р-1)( q -1)

Функция Эйлера показывает количество целых положительных чисел от1 до n, которые не имеют ни одного общего делителя, кроме 1.

Шаг 4. Выбирается число е, которое должно взаимно простым со значением функции Эйлера и меньшим, чем f(р q.)

Шаг 5. Определяется число d, удовлетворяющее соотношению

е * d ( mod f (р q .))=1

Числа е и n принимаются в качестве открытого ключа. В качестве секретного ключа используются числа d и n.

Шаг 6. Исходная информация независимо от её физической природы представляется в числовом двоичном виде. Последовательность бит разделяется на блоки длиной L бит, где L – наименьшее целое число, удовлетворяющее условию L ³ log₂(n.+1); Каждый блок рассматривается как целое положительное число X(i), принадлежащее интервалу (0, n-1). Таким образом, исходная информация представляется последовательностью чисел X(i), (i = 1.I).Значение I определяется длиной шифруемой последовательности.

Шаг 7. Зашифрованная информация получается в виде последовательности чисел Y(i)= (Y(i))^e (mod n).

Шаг 8. Для расшифрования информации используется следующая зависимость Х(i)= (Y(i))^e (mod n).

Рассмотрим числовой пример применения метода RSA для криптографического закрытия информации, в котором для простоты вычислений использованы минимально возможные числа. Пусть требуется зашифровать сообщение на русском языке ПРЕДЕЛ.

Сообщение: ПРЕДЕЛ

Простые числа p и q - 3,11

Зашифруем и расшифруем сообщение "ПРЕДЕЛ" по алгоритму RSA:

1) Выберем p=3 and q=11.

2)Вычислим открытую компоненту ключа: n = 3*11=33.

3) Определим функцию Эйлера: (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3).

4) Выберем число е по следующей формуле: (e*3) mod 20=1. е будет равно 7: (e=7).

Числа е и n принимаются в качестве открытого ключа, d и n используются в качестве секретного ключа.

Таблица 1.2 – Позиции букв в алфавите

Буквы алфавита

Номер буквы

Буквы алфавита

Номер буквы

5) Представим шифруемое сообщение как последовательность чисел в диапазоне от 0 до 32: 16, 17, 6, 5, 6, 12,ПРЕДЕЛ

Для представления чисел в двоичном виде требуется 6 двоичных разрядов, так как в русском алфавите используются 33 буквы, поэтому исходный текст имеет вид: 010000, 010001, 000110, 000101, 000110, 001100.

Длина блока L определяется как минимальное число из целых чисел, удовлетворяющих условию L ³ log₂(33+1); L=6

Теперь зашифруем сообщение, используя открытый ключ {7,33}

Y 1 = (16⁷) mod 33 = ;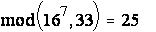

Y2 = (17⁷) mod 33 = ;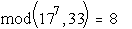

Y3 = (6⁷) mod 33 = ;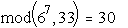

Y4 = (5⁷) mod 33 = ;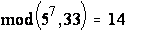

Y 5 = (6⁷) mod 33 = ;

Y 6 = (12^7) mod 33 = ;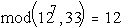

Расшифруем полученные данные, используя закрытый ключ {3,33}.

Y1 = (25³) mod 33 = ;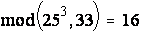

Y2 = (8³) mod 33 = ;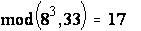

Y3 = (30³) mod 33 = ;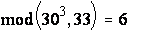

Y4 = (14³) mod 33 = ;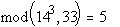

Y5 = (30³) mod 33 = ;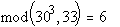

Y6 = (12³) mod 33 = ;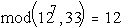

Данные расшифрованы, сопоставим последовательность <16, 17, 6, 5, 6, 12> с последовательностью букв нашего алфавита. Получили слово ПРЕДЕЛ

Хеш-функции. Хеширование

Содержание:

Вычисления цифровой подписи

П Р Е Д Е Л

16 17 6 5 6 12

00010000, 00010001, 00000110, 00000101, 00000110, 0001100 :

в) Разбить байт пополам, добавив в начало полубайта единицы и получить хешируемые блоки М_i:

M ₁	M ₂	M ₃	M ₄	M₅	M₆
11110001	11110000	11110001	11110001	11110000	11110110
M ₇	M ₈	M ₉	M ₁₀	M ₁₁	M ₁₂
11110000	11110101	11110000	11110110	11110000	11111100

3) Выполнение интеративных шагов :

Первая итерация

М₁	11110001
Å
Н₀=0	00000000
Н₀Å М₁	11110001=241₁₀
[(H₀Å M₁)²] (mod 33)	241² mod 33 = 10
Н₁	10₁₀=00001010

Вторая итерация

М₂	11110000
Å
Н₁	00001010
Н₁Å М₂	11111010=250₁₀
[(H₁Å M₂)²] (mod 33)	250² mod 33 = 19
Н₂

00010011

Третья итерация

М₃	11110001
Å
Н₂	00010011
Н₂Å М₃	11100010=226₁₀
[(H₂Å M₃)²] (mod 33)	226² mod 33 = 28
Н₃	000 11100

Четвертая итерация

М₄	11110001
Å
Н₃	00011100
Н₃Å М₄	11101101=237₁₀
[(H₃Å M₄)²] (mod 33)	237² mod 33 = 6
Н₄	00000110

Пятая итерация

М₅	11110000
Å
Н₄	00000110
Н₄Å М₅	11110110=246₁₀
[(H₄ Å M₅)²] (mod 33)	246² mod 33 = 15
Н₅	0000 1111

Шестая итерация

М₆	11110110
Å
Н₅	00001111
Н₅Å М₆	11111001=249₁₀
[(H₅Å M₆)²] (mod 33)	249² mod 33 =18
Н₆

000 10010

Седьмая итерация

М₇	11110000
Å
Н₆	00010010
Н₆Å М₇	11100010 = 226₁₀
[(H₆Å M₇)²] (mod 33)	226² mod 33 = 28
Н₇	000 11100

Восьмая итерация

М₈	11110101
Å
Н₇	00011100
Н₇Å М₈	11101001= 233
[(H₇Å M₈)²] (mod 33)	233² mod 33 = 2
Н₈	00000010

Девятая итерация

М₉	11110000
Å
Н₈	00000010
Н₈Å М₉	11110010 = 242₁₀
[(H₈Å M₉)²] (mod 33)	242² mod 33 = 11
Н₉	00001011

Десятая итерация

М₁₀	11110110
Å
Н₉	00001011
Н₉Å М₁₀	11111101 = 253
[(H₉Å M₁₀)²] (mod 33)	253² mod 33 = 22
Н₁₀	00010110

Одиннадцатая итерация

М₁₁	11110000
Å
Н₁₀	00010110
Н₁₀Å М₁₁	11100110 =230₁₀
[(H₁₀ÅM₁₁)²] (mod 33)	230² mod 33 = 32
Н₁₁	00 100000

Двенадцатая итерация

М₁₂	11111100
Å
Н₁₁	00100000
Н₁₁Å М₁₂	11011100 = 220₁₀
[(H₁₁ÅM₁₂)²] (mod 33)	220² mod 33 = 22
Н₁₂	00010110

Таким образом, исходное сообщение ПРЕДЕЛ имеет хеш – код m =22.

Вычисления цифровой подписи

Для вычисления цифровой подписи используем следующую формулу:

S=m^d (mod n) = 22³ mod 33 = 22

Пара ( M , S ) передается получателю как электронный документ М, подписанный цифровой подписью S , причем подпись S сформирована обладателем секретного ключа d .

Получив пару (M, S), получатель вычисляет хеш – код сообщения М двумя способами:

1) Восстанавливает хеш – код m’, применяя криптографическое преобразование подписи S с использованием открытого ключа e:

m’=S^e (mod n) =22⁷ mod 33 = 22

2) Находит результат хеширования принятого сообщения с помощью той же хеш – функции: m = H ( M ) =22.

При равенстве вычисленных значений m ’ и m получатель признает пару ( M , S ) подлинной.

Контрольные вопросы

1. Изложите принципиальную схему организации секретной связи с использованием системы шифрования с открытым ключом.

2. Изложите принципиальную схему организации обмена документами, заверенными цифровой подписью.

3. Перечислите основные требования, предъявляемые к хеш-функции, пригодной для использования при вычислении цифровой подписи документа.

4. Каким образом с помощью криптосистемы RSA можно организовать передачу шифрованных сообщений, подлинность которых подтверждена цифровой подписью? Приведите примеры.
Расчетно-графическое задание № 2

Таблица 1.1 Исходные данные для числа g :

i	0	1	2	3	4	5	6	7	8	9
g	1	3	5	11	23	29	41	101	113	179

Таблица 1.2 Исходные данные для чисел X_A, X_B_, X_C_, X_D_, X_E:

j	0	1	2	3	4	5	6	7	8	9
X	7	11	13	17	19	29	31	37	39	41

Методические указания к решению задания 2.1

Первая система с открытым ключом — система Диффи-Хеллмана.

Эта криптосистема была открыта в середине 70-х годов американскими учеными Диффи (Whitfield Diffie) и Хеллманом (Martin Hell-man) и привела к настоящей революции в криптографии и ее практических применениях. Это первая система, которая позволяла защищать информацию без использования секретных ключей, передаваемых по защищенным каналам. Для того чтобы продемонстрировать одну из схем применения таких систем, рассмотрим сеть связи с N пользователями, где N — большое число. Пусть мы хотим организовать секретную связь для каждой пары из них. Если мы будем использовать обычную систему распределения секретных ключей, то каждая пара абонентов должна быть снабжена своим секретным ключом, т.е. всего потребуется 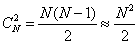ключей.

Если абонентов 100, то требуется 5000 ключей, если же абонентов 10⁴ , то ключей должно быть 5∙10⁷. Мы видим, что при большом числе абонентов система снабжения их секретными ключами становится очень громоздкой и дорогостоящей.

Диффи и Хеллман решили эту проблему за счет открытого распространения и вычисления ключей. Перейдем к описанию предложенной ими системы.

Пусть строится система связи для абонентов А,В,С,... .У каждого абонента есть своя секретная и открытая информация. Для организации этой системы выбирается большое простое число р и некоторое число g, 1 < g < р — 1, такое, что все числа из множества {1, 2, ∙ ∙ ∙ ,р — 1} могут быть представлены как различные степени g mod p (известны различные подходы для нахождения таких чисел g, один из них будет представлен ниже). Числа р и g известны всем абонентам.

Абоненты выбирают большие числа X_a,X_b,X_c, которые хранят в секрете (обычно такой выбор рекомендуется проводить случайно, используя датчики случайных чисел). Каждый абонент вычисляет соответствующее число Y, которое открыто передается другим абонентам,

Y_А = g^Xa mod р ,

Y_B = g^Xb mod р.. (1)

Yс = g^Xc mod р.

В результате получаем следующую таблицу.

Таблица 1.3 Ключи пользователей в системе Диффи-Хеллмана

Абонент	Секретное число	Открытый ключ	Закрытый ключ
A B C	X_A X_B X_C	Y_A Y_B Y_C	Z_AB, Z_AC Z_BA, Z_BC Z_CA, Z_CB

Допустим, абонент А решил организовать сеанс связи с В, при этом обоим абонентам доступна открытая информация из табл. 2. Абонент А сообщает В по открытому каналу, что он хочет передать ему сообщение. Затем абонент А вычисляет величину

Z_AB = (Y_B)^ХА modp (2)

Никто другой, кроме А, этого сделать не может, так как число Х_А секретно.

В свою очередь, абонент В вычисляет число

Z_BA = (Y_A)^XBmodp (3)

На рисунке 1 представлена схема обмена ключами в системе Диффи-Хеллмана.

Остановимся теперь на упомянутой выше задаче выбора числа р.

При произвольно заданном g она может оказаться трудной задачей, связанной с разложением на простые множители числа g - 1.

Дело в том, что для обеспечения высокой стойкости рассмотренной системы число g - 1 должно обязательно содержать большой простой множитель.

Поэтому часто рекомендуют использовать следующий подход.

Число р выбирается таким, чтобы выполнялось равенство

р=2q+1 (где q- также простое число)

и были справедливы неравенства

1 < g < р - 1 и g^q mod р 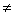1.

Для того чтобы система была устойчива к криптоанализу, необходимо выбирать число р очень большим.

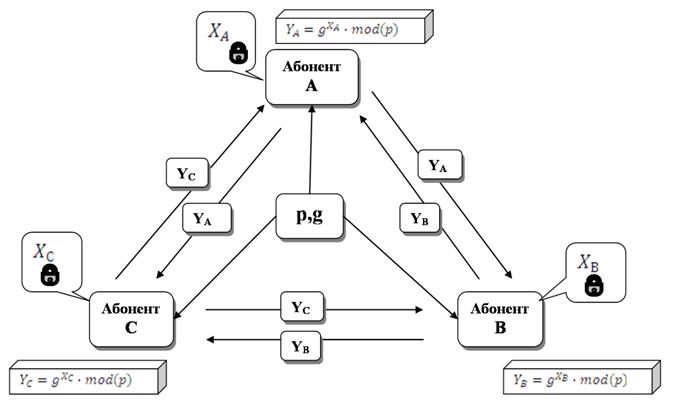
Рисунок 1 - схема обмена ключами в системе Диффи-Хеллмана

Пример 2.1. Пусть g = 43. Выберем параметр p. Попробуем взять q=17 401.

Соответственно р=2*17 401+1=34 803. Проверим: 43¹⁷⁴⁰¹ mod 34 803 = 17 746. Необходимые условия выполняются, значит, такое р подходит. Итак, мы выбрали параметры р = 34 803, g = 43. Теперь каждый абонент выбирает секретное число и вычисляет соответствующее ему открытое число. Пусть выбраны Х_A = 7, Х_B = 13. Вычисляем Y_A = 43⁷ mod 34 803 = 11 689, Y_B = 43¹³ mod 34 803 = 14 479. Пусть А и В решили сформировать общий секретный ключ. Для этого А вычисляет Z_AB = 14479⁷ mod 34 803=6 415, а В вычисляет Z_BA = 11 689¹³ mod 34 803 = 6 415. Теперь они имеют общий ключ 6 415, который не передавался по каналу связи.

Контрольные вопросы

1. Какими преимуществами перед другими алгоритмами с закрытым ключом обладает система Диффи-Хеллмана?

2. Дайте краткую характеристику системы Диффи-Хеллмана.

3. Объясните, почему число р, необходимое при вычислении секретных ключей, следует выбирать большим?

2.2 Шифрование по алгоритму Шамира

Зашифровать сообщение по алгоритму Шамира для трех абонентов, взяв значение сообщения m и значение p из таблиц 2.1 и 2.2 соответственно. По номеру j (последняя цифра номера зачетной книжки) выбирается требуемое для реализации этого алгоритма число р. По i (предпоследняя цифра номера зачетной книжки) студент выбирает сообщение для зашифровывания, передаваемое первым абонентом. Выбор сообщений для других абонентов производится циклически, согласно процедуре (i + 1). Например, последние цифры номера зачетной книжки – (63). Выбираем для трех абонентов p = 41, m_A=24, m_B=24, m_C=24.

Таблица 2.1 – исходные данные для выбора сообщений ( m )

i	0	1	2	3	4	5	6	7	8	9
Сообщение ( m )	12	14	16	18	20	22	24	26	28	30

Таблица 2.2 – исходные данные для выбора числа р

j	0	1	2	3	4	5	6	7	8	9
р	29	31	37	41	43	47	49	51	53	57

Таблица 3.1 Исходные данные для выбора сообщений

i	0	1	2	3	4	5	6	7	8	9
Сообщение ( m)	5	7	9	11	13	3	15	11	15	13

Таблица 3.2 Исходные данные для выбора чисел p и g

j	0	1	2	3	4	5	6	7	8	9
p, g	29,11	1 7 ,11	21,11	13, 11	23,17	23,7	29,7	17,7	19,7	1 9,11

Список литературы

1.Романец Ю. В. Защита информации в компьютерных системах и сетях. /Под ред. В.Ф. Шаньгина. – М: Радио и связь 1999

2.Петраков А.В. Основы практической защиты информации. 2-е издание Учебн. Пособие. – М: Радио и связь 200

3. Рябко Б. Я., Фионов А.Н. Криптографические методы защиты информации. –М: Горячая линия- Телеком, 2005.