{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
// MessageBox.Show(" button1_Click");
TabFunc tb = new TabFunc();
tb.A = double.Parse(textBox1.Text);
tb.B = double.Parse(textBox2.Text);
tb.H = double.Parse(textBox3.Text);
tb.TabF(listBox1);
textBox4.Text = Convert.ToString(tb.Xmin);
textBox5.Text = Convert.ToString(tb.Min);
textBox6.Text = Convert.ToString(tb.Count);
}
}
public class TabFunc
{
public double A { get; set; }
public double B { get; set; }
public double H { get; set; }
public double Xmin { get; set; }
public double Min { get; set; }
public int Count { get; set; }
private double f(double x)
{
return 10 * Math.Sin(3 * x) * Math.Exp(-5 * x);
}
public void TabF(ListBox lb)
{
lb.Items.Clear();
double x = A;
Min = f(x); Xmin = x;
Count = 0;// можно и без этого
while (x<=B)
{
double y = f ( x );
lb . Items . Add ( x . ToString (" F 4") + " " + y . ToString (" E "));//форматный вывод
if (Min > y)
{
Min = y;
Xmin = x;
}
if (y > 0) Count++;// равносильно Count= Count+1
x += H ;//равносильно x = x + H
}
}
}
}
В этом примере используется метод класса double ToString (), позволяющий преобразовывать числовые значения по некоторым форматам: "F4" - вывод числа с фиксированной точкой, "E" – формат с плавающей точкой.
Результат работы этого приложения приведен на рис. 7.4.
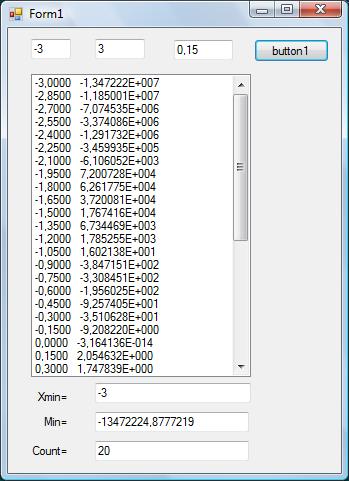
Рис. 7.4. Результат работы приложения из примера 7.4
Пример 7.5. Следующий пример использования операторов цикла состоит в вычислении суммы бесконечного ряда с требуемой точностью. Продемонстрируем его на примере вычисления функции exp( x ).
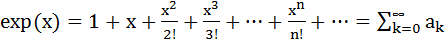, (7.1)
где
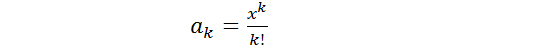(7.2)
Запишем конечную сумму из N элементов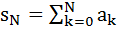 
, и тогда
.
Как на практике вычислять такую сумму бесконечного числа слагаемых? Надо бесконечное время, которого, естественно, нет. Следовательно, в таком виде задачу решить нельзя. Что делать? Заменим задачу на следующую: вычислить сумму ряда с требуемой точностью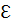 
. Что это значит? Здесь рассуждают следующим образом: будем получать набор конечных сумм 
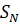для N=1,2,3, … и прекратим этот процесс, то есть будем считать, что решили задачу с точностью 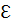, если выполняется такое условие: две соседние суммы 
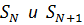отличаются меньше, чем на величину требуемой точности. Математики будут ругаться, но если сказать «просто», то рассуждать можно так: что прибавляли очередной элемент, что не прибавляли, разница уже маленькая. Это выглядит так:
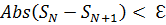
или
Abs (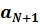 
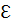) < (7.3)
с точки зрения классической математики это не очень строго, можно привести примеры, где этого не проходит, но будем считать, что ряды «хорошие».
Далее, в примере, как и во многих подобных задачах, непосредственный подсчет очередного члена связан с вычислительными трудностями: значение x надо возводить в большую степень, надо вычислять факториалы больших чисел. Само по себе это нехорошо, а еще может так случиться, что оба полученные значения будут большими и их деление может привести к существенным вычислительным ошибкам. От всего этого можно уйти, если использовать рекуррентные вычисления, которые позволяют получать последовательность значений с использованием принципа: следующее значение вычисляют, используя значение на предыдущем, а может быть на нескольких предыдущих шагах. Это удобно делать, каждый раз умножая предыдущий элемент ряда на множитель, то есть
* 
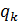, (7.4)
где 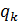и есть этот множитель. Индекс k показывает, что этот множитель зависит от номера элемента и что говорит о том, что это не есть геометрическая прогрессия. Записав явное выражение (7.2) для элемента с номером k+1 и элемента с номером k, можно найти этот множитель:
= 
= 
= 
.
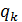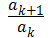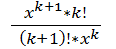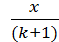Чтобы запустить процесс рекуррентных вычислений (7.4), еще надо задать начальные значения счетчика k и значение начального элемента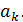 
Из (7.1) следует, что k = 0 и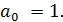 
Окончательно, вычисления элементов ряда по рекуррентной формуле выглядит так
* 
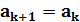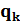, k= 0,1,2,. . . , 
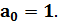(7.5)
Выражение (7.5) есть рекуррентная формула для вычисления элементов ряда.
Но это еще не все. Надо научиться вычислять сумму этих элементов. Представляется, что для вычисления суммы удобно использовать следующее выражение:
= 
, 
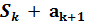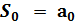. (7.6)
Итак, как вычислять элементы ряда и как менять номер элемента знаем - формула (7.5), как вычислять их сумму знаем – формула (7.6). Понятно, что это надо будет делать в цикле. Когда заканчивать цикл тоже знаем – формула (7.3).
Составим блок-схему решения задачи, она прямо «вываливается» из трех этих условий (рис. 7.5).
Рис. 7.5 а,б. Два варианта блок-схем вычисления суммы ряда с требуемой точностью
На рис. 7.5 представлены блок-схемы вычисления суммы ряда. На рис. 7.65а с использованием цикла с предусловием, на рис. 7.6б с циклом с постусловием.
В C#, как и в других языках программирования, есть оператор цикла for. Его структура следующая:
for (инициализация счетчиков; условие продолжения; изменение счетчиков)
блок операторов;
Здесь for – служебное слово, «инициализация счетчиков» - присваивание счетчикам цикла начальных условий, «условие продолжение» - условное выражение, определяющее продолжительность выполнения цикла, «изменение счетчиков» - выражения, определяющие изменения счетчиков цикла после каждой итерации, «блок операторов» - тело цикла.
Работает этот оператор так: перед началом цикла счетчикам цикла присваиваются начальные значения, затем проверяется условие продолже-ния. Если оно истинно, то выполняется тело цикла, после чего счетчики изменяют свои значения в соответствии с «изменением счетчиков». Если условие продолжения ложно, оператор завершает свою работу.
Особенностью работы этого оператора является то, что счетчиков цикла может быть несколько, и то, что <условие продолжения> есть логическое выражение. Все это приводит к тому, что оператор for полностью дублирует оператор цикла с предусловием. А для чего он тогда нужен? Для удобства: всё, что касается цикла записано в одной строке, а «не разбросано» по телу цикла, как в цикле с предусловием.
На рис. 7.5в представлена блок-схема вычисления суммы ряда с использованием цикла for.
Рис. 7.5 в. Еще один вариант блок-схемы вычисления суммы ряда с требуемой точностью
Теперь решение задачи в трех вариантах: с префиксной, постфиксной формами цикла и с счетным циклом for. Иногда используют и такую терминологию.
В классе ClMyExp заведены поля для хранения исходных данных и результатов, а также три метода, реализующие алгоритмы, соответствующие блок-схемам рис. 7.6. На форме организованы три кнопочки, в каждой из которых инициируется по объекту класса ClMyExp.
Пример 7.6.
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Windows.Forms;
Namespace WindFormExp
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
ClMyExp ExpWhile=new ClMyExp();
ExpWhile.X = double.Parse(textBox1.Text);
ExpWhile.Eps = double.Parse(textBox2.Text);
ExpWhile.S = ExpWhile.MyExpWhile();
textBox3.Text =Convert.ToString(ExpWhile.S) + " " + Convert.ToString(ExpWhile.N);
double xx = Math.Exp(ExpWhile.X);
textBox4.Text = Convert.ToString(xx);
}
private void button2_Click(object sender, EventArgs e)
{
ClMyExp ExpFor = new ClMyExp();
ExpFor.X = double.Parse(textBox1.Text);
ExpFor.Eps = double.Parse(textBox2.Text);
ExpFor.S = ExpFor.MyExpFor();
textBox5.Text = Convert.ToString(ExpFor.S) + " " + Convert.ToString(ExpFor.N);
double xx = Math.Exp(ExpFor.X);
textBox4.Text = Convert.ToString(xx);
}
private void button4_Click(object sender, EventArgs e)
{
ClMyExp ExpDoWhile = new ClMyExp();
ExpDoWhile.X = double.Parse(textBox1.Text);
ExpDoWhile.Eps = double.Parse(textBox2.Text);
ExpDoWhile.S = ExpDoWhile.MyExpDoWhile();
textBox6.Text = Convert.ToString(ExpDoWhile.S) + " " + Convert.ToString(ExpDoWhile.N);
double xx = Math.Exp(ExpDoWhile.X);
textBox4.Text = Convert.ToString(xx);
}
}
public class ClMyExp
{
public double X{get;set;}
public double Eps{get;set;}
public double S{get;set;}// приближенное значение суммы
public int N{get;set;} // количество элементов ряда, вошедших в сумму
public double MyExpWhile()
{
N=0;
double a=1;
double S=a;
while (Math.Abs(a)>Eps)
{
a = a * X / (N + 1);
S = S+a;
N++;
}
return S;
}
public double MyExpFor()
{
double a = 1;
double S = a;
for (int n = 0; Math.Abs(a) > Eps; n++)
{
a = a * X / (n + 1);
S = S + a;
this.N = n;
}
return S;
}
public double MyExpDoWhile()
{
N = 0;
double a = 1;
double S = a;
do
{
a = a * X / (N + 1);
S = S + a;
N++;
}
while (Math.Abs(a) > Eps);
return S;
}
}
}
Обратите внимание, что в методе с циклом for переменная n является локальной переменной, объявленной внутри цикла, и «работает» только внутри цикла. Поэтому внутри цикла используется оператор присваивания this.N = n, причем то, что N есть свойство объекта класса ClMyExp подчеркивается служебным словом this, которое означает то, что N есть свойство текущего объекта (см. Лекцию 6, пример 6.2). В принципе можно было обойтись и без этого this.
Результаты выполнения такого приложения приведены на рис. 7.6.
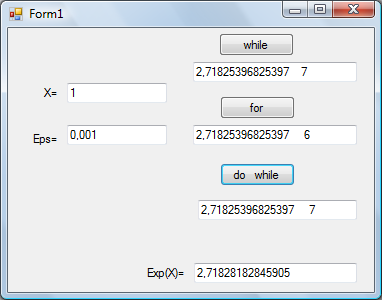
Рис. 7.6. Результаты работы программы вычисления суммы ряда с требуемой точностью в трех вариантах
Приближенные значения экспоненты во всех вариантах одинаковые и отличаются от значения, полученного с использованием метода Exp() класса Math не больше, чем на требуемую точность, а вот количество вошедших в сумму элементов в цикле for отличается на единицу от других результатов. Проанализируйте, пожалуйста, в чем причина?
Дата: 2019-11-01, просмотров: 201.
